Тема: Простые и составные задачи

План:

1. Система простых задач начального курса математики (различные классификации: традиционный, подход П.М. Эрдниева, подход Н.Б. Истоминой).

2. Содержание упражнений подготовительного этапа при переходе от простых задач к составным.

3. Первое знакомство с составной задачей (ответ подготовить в виде плана-конспекта).

Рекомендательная литература

1. Свечников А.А. Решение математических задач в 1-3-х классах. – М., 1976. – С. 45-52.

2. Истомина Н.Б. Работа над составной задачей //Начальная школа. – 1988. - №2. – С. 44-49. (Подготовительный этап).

3. Уткина Н.Г. Составные задачи в 1-м классе // Изучение трудных тем по математике в 1-3-х классах. – М., 1982. – С. 45-52.

4. Гребенникова Н.Л. Опоры-перфокарты в обучении решению задач // Начальная школа. – 1992. - №7-8. – 38 с.

5. Смирнова С.И. Использование чертежа при решении простых задач // Начальная школа. – 1998. - №5. – С. 53-58.

Во 2 классе четырехлетней начальной школы впервые вводятся составные задачи (напомним, что составными называются задачи, которые решаются в два и более действий). Рассмотрим методику поэтапной работы с такими задачами:

Подготовительный этап. На этом этапе работа ведется с парами простых задач, таких, что ответ первой задачи является одним из данных чисел второй задачи. Приведем пример пары таких задач:

1) У Саши было 6 тетрадей в клетку и 2 тетради в линейку. Сколько всего тетрадей было у Саши?

2) У Саши было 8 тетрадей. 3 тетради он сдал учителю. Сколько тетрадей у него осталось?

В этой паре ответ первой задачи (8 тетрадей) является данным условием второй задачи.

На основе пары таких простых задач легко ввести составную задачу: У Саши было 6 тетрадей в клетку и 2 тетради в линейку. 3 тетради он сдал учителю. Сколько тетрадей у него осталось?

Основная трудность в решении таких задач состоит в том, что ребенок Перове действие выполняет в уме, а общее решение записывает так:

8 – 3 = 5 (т.)

На вопрос: «Откуда взялось число 8? Ведь его в условии задачи не было», чаще всего дети дают такой ответ «Но ведь 6 и 2 будет 8».

Решение пар простых задач позволяет предупредить эту ошибку и помочь детям осознать тот факт, что одним действием такую задачу решить нельзя.

Этап знакомства с составной задачей. Дети знакомятся с составной задачей на примере двух вариантов задач:

1) составной задачи, в которой первое действие является простой задачей на уменьшение числа на несколько единиц, а второе – простой задачей на нахождение суммы («В первой тарелке 5 груш, а во второй на 2 груши меньше. Сколько груш в двух тарелках?»);

2) составной задачи, в которой первое действие является простой задачей на нахождение суммы, а второе – простой задачей на нахождение остатка («Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку. Сколько флажков осталось?»). на примере этих задач рассмотрим методические особенности работы с ними.

Процесс работы над задачей состоит из следующих основных этапов:

1) Краткая запись условия задачи, которая помогает лучше разобраться в ее содержании.

2) Разбор задачи, в ходе которого выявляются отношения между данными и искомой величиной, осуществляется выбор арифметического действия.

3) Запись решения задачи и полученного ответа.

Для первого варианта составной задачи эти этапы будут выглядеть следующим образом.

Текст задачи

«В первой тарелке 5 груш, а во второй на 2 груши меньше. Сколько груш в двух тарелках?»

Краткая запись условия

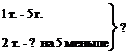
Разбор задачи

- Что известно в задаче? (В первой тарелке 5 груш, а во второй на 2 груши меньше.)

- Какой главный вопрос в задаче? (Сколько груш в двух тарелках?)

- Можем ли мы сразу ответить на этот вопрос? (Нет.)

- Что для этого нужно знать (Сколько груш в каждой тарелке.)

- Сколько груш в первой тарелке? (5.)

- А что сказано про вторую? (В ней на 2 груши меньше.)

- Как узнать, сколько груш во второй тарелке? (Нужно из 5 вычесть 2.)

- Как потом узнать, сколько груш в двух тарелках? (Нужно к тому, что получится в первом действии, прибавить 5.)

- Верно. Итак, сколько действий в этой задаче? (Два.)

- Какое первое действие? (Из 5 вычтем 2.)

- Что мы узнаем, выполнив это действие? (Сколько груш во второй тарелке.)

- Что будем делать во втором действии? (К результату первого действия прибавим 5.)

- Что узнаем, выполнив это действие? (Сколько груш в двух тарелках.)

Запись решения задачи

(с пояснением)

1) 5 – 2 = 3 (г.) – было во 2 тарелке.

2) 5 + 3 = 8 (г.) – всего в двух тарелках.

Ответ: 8 груш.

Приведем пример реализации данных этапов для второго варианта составной задачи.

Текст задачи

«Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку. Сколько флажков осталось?»

Краткая запись условия

Вырезали – 6 ф. и 4 ф.

Повесили – 3 ф.

Осталось - ?

Разбор задачи

(синтетический способ)

- Что известно в задаче? (Вырезали 6 красных флажков и 4 синих. 3 флажка повесили на елку.)

- Какой главный вопрос в задаче? (Сколько флажков осталось?)

- Зная, что вырезали 6 красных флажков и 4 синих, что мы можем узнать? (Сколько всего флажков вырезали.)

- Каким действием это узнаем? (Сложением.)

- Зная, сколько флажков вырезали, и что 3 флажка их них повесили на елку, что мы можем найти? (Сколько флажков осталось.)

- Каким действием найдем? (Вычитанием.)

Запись решения задачи

(составлением выражения)

(6 + 4) – 3 = 7 (ф.)

Ответ: 2 ф.

Как видим, на примере, двух вариантов составных задач представлены основные способы краткой записи условия, разбора и записи решения, которые используются во 2 классе. Рассмотрим их более подробно.

Краткая запись условия задачи начинает вводиться постепенно. Сначала для этого используются начальные буквы опорных слов, а затем и сами опорные слова: «Было», «подарил», «продали», «улетело», «осталось» и т.д. При работе над вторым вариантом задачи использована такая краткая запись условия. Однако она не всегда помогает отразить реальные отношения между данными и искомыми величинами в задаче. Поэтому при решении как простых, так и составных задач мы рекомендуем использовать краткую запись в виде схем, чертежей, отрезков. Пример такой краткой записи условия приведен в первой задаче.

В начальной школе используются два основных способа рассуждений при разборе задачи: аналитический и синтетический. Аналитический способ более подробный, он начинается с главного вопроса задачи и постепенно восходит к величинам, данным в условии. Он используется, как правило, при освоении нового вида задачи. При синтетическом способе рассуждений мысль движется в обратном порядке: от условия задачи к главному вопросу. Этот способ является менее развернутым и пользуется, как правило, при разборе уже знакомых задач.

После разбора задачи переходят к записи ее решения. В настоящее время в начальной школе наиболее распространенной является запись решения по действиям с кратким пояснением результата действия. Этот способ показан в первой задаче. Освоив запись решения по действиям, можно переходить к записи решения способом составления выражения. В выражении выполняются те же действия, но они представлены в свернутом виде, поэтому данный способ требует более высокого уровня умения решать задачи.