Полупространства. евклидово пространство.

Полупространство— совокупность точек евклидова многомерного пространства, лежащих по одну сторону от некоторой плоскости, разделяющей это пространство. Различают открытое изамкнутое П. В первом случае П. это множество точек x_i(i=1,…,n), координаты которых удовлетворяют неравенству Σa_ix_i<d или неравенству Σa_ix_i>d. Во втором случае это множество точек, удовлетворяющих неравенству Σa_ix_i≥ d, или неравенству Σa_ix_i≤ d ,то есть П., включающее разделяющую гиперплоскость. В обоих случаях принимается, что параметры a₁,…,a_n не могут быть одновременно равны нулю.

Определение.Линейное пространство, на котором задано скалярное произведение, называется евклидовым пространством.

Примером евклидова пространства служит пространство 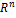, в котором скалярное произведение векторов 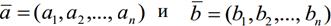задаетсясоотношением: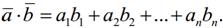

19.n-мерные векторы и действия над ними, n-мерное линейное векторное пространствоR⁽ⁿ⁾. Линейные операторы. Линейная комбинация векторов.

n-мерным вектор - любая упорядоченная совокупность n действительных чисел а1,а2..аn

n-мерное линейное векторное пространствоR⁽ⁿ⁾:

Все n-мерные линейные пространства “устроены” одинаково - как пространство Rⁿ векторов-столбцов из n действительных чисел, т.е. что все они изоморфны пространству Rⁿ .

Линейные пространства X и Y называются изоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что если векторам x и x' из X соответствуют векторы y и y' из Y, то вектору x + x' соответствует вектор y + y' и при любом a вектору a x 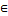X соответствует вектор a 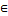y Y .

Изоморфизм n-мерных линейных пространств пространству Rⁿ означает, что соотношения между элементами n-мерного линейного пространства и операции с ними можно изучать как соотношения между векторами из Rⁿ и операции с ними и что всякое утверждение относительно векторов из Rⁿсправедливо для соответствующих элементов любогоn-мерного линейного пространства.

Например, доказано, что система векторов e₁, e₂, ..., e_n из Rⁿ

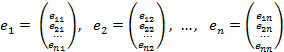
образует базис в Rⁿ тогда и только тогда, когда отличен от нуля определитель матрицы, со столбцами e₁, e₂, ..., e_n:

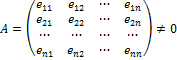
Линейная комбинация векторов:

20.Линейная зависимость и линейная независимость системы векторов. Свойства линейной зависимости и линейной независимости векто­ров.

Свойства линейной зависимости и линейной независимости векторов:

1. Если к линейно зависимой системе векторов 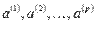добавить несколько векторов, то полученная система будет линейно зависимой.

2. Если из линейно независимой системы векторов 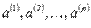исключить несколько векторов, то полученная система будет линейно независимой.

3. Если в системе векторов 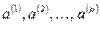есть хотя бы один нулевой вектор, то такая система линейно зависимая.

4. Если система векторов 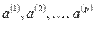линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов 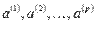линейно независима, то ни один из векторов не выражается через остальные.

21.Понятие базиса n - мерного векторного пространства. Разложение вектора про­странства R⁽ⁿ⁾ по векторам базиса.