Б-22 Математические операции над случайными величинами.

Вначале введем понятие независимости случайных величин.

Две случайные величины называются независимыми, если закон распределения одной из них не меняется от того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми. Например, если имеются билеты двух различных денежных лотерей, то случайные величины X и Y, выражающие соответственно выигрыш по каждому билету, будут независимыми, так как при любом выигрыше по билету одной лотереи (например, при X=x_i) закон распределения выигрыша по другому билету (Y) не изменится. Если же случайные величины X и Y выражают выигрыш по билетам одной денежной лотереи, то в этом случае X и Y являются зависимыми, ибо любой выигрыш по одному билету (X=x_i) приводит к изменению вероятности выигрыша по другому билету (Y), то есть к изменению закона распределения Y.

Определим математические операции над ДСВ.

Произведением kX случайной величины Х на постоянную величину k называется случайная величина, которая принимает значения kx_i с теми же вероятностями p_i (i=1, 2, …, n).

m-й степенью случайной величины Х, то есть Х^m, называется случайная величина, которая принимает значение с теми же вероятностями p_i (i=1, 2, …, n).

Суммой (разностью или произведением) случайных величин Х и Y называется случайная величина, которая принимает все возможные значения вида x_i+y_j (x_i-y_j или x_i•y_j), где i=1, 2, …, n; j=1, 2, …, m, с вероятностями p_ij того, что случайная величина Х примет значение x_i, а Y - значение y_j: p_ij=Р[(X=x_i) (Y=y_j)].

Если случайные величины Х и Y независимы, то есть независимы любые события X=x_i, Y=y_j, то по теореме умножения вероятностей для независимых событий

p_ij=Р(X=x_i)•Р(Y=y_j) = p_i•p_j.

Б-23 Математическое ожидание дискретной случайной величины.

Пусть задан закон распределения случайной величины x.

x	х1	х2	х3	¼	хn
P	p1	p2	p3	¼	pn

Математическое ожидание Мx (или М(x)) случайной величины x определяется формулой

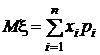
Рассмотрим пример. Пусть в некотором магазине, торгующем электробытовой техникой, получены статистические данные о числе проданных холодильников в каждый день месяца (условно считаем, что месяц состоит из 30 рабочих дней). Эти данные собраны в таблицу:

Количество проданных холодильников
Число дней, в которые было продано столько холодильников

По этой таблице легко подсчитать число холодильников, проданных в магазине за месяц: 0×3+1×7+2×8+3×9+4×2+5×1 = 63. Чтобы подсчитать среднее число холодильников, продававшихся в один день месяца, нужно эту сумму разделить на 30, в результате получим 2,1. Если в приведенной таблице каждое число второй строки поделить на 30, то получится последовательность дробей

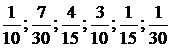, каждая из которых представляет собой так называемую относительную частоту, с которой в данный месяц появлялся приведенный в верхней строке объём продаж. Очевидно, что если просуммировать все произведения чисел, стоящих в первой строке таблицы, на их относительные частоты, то получится то же среднее число продававшихся в один день холодильников:

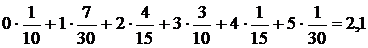
Если бы в последней формуле относительные частоты рассчитывались не для одного месяца, а для существенно большего срока, то при некоторых условиях (например, при отсутствии кризисных явлений, существенно влияющих на спрос населения на дорогостоящие товары) эти относительные частоты можно было бы считать довольно близкими к вероятностям соответствующих значений объёма продаж. Таким образом, приходим к выводу, что математическое ожидание случайной величины – это в некотором смысле её среднее значение. Следует отметить, что случайная величина может вообще не принимать значения, равного её математическому ожиданию. Так, например, случайная величина, принимающая только значения 1 и –1, каждое – с вероятностью 0,5, имеет математическое ожидание, равное нулю.

Б-24 Дискретная случайная величина, закон и функция распределения

Дискретной называют случайную величину, значения которой изменяются не плавно, а скачками, т.е. могут принимать только некоторые заранее определённые значения. Например, денежный выигрыш в какой-нибудь лотерее, или количество очков при бросании игральной кости, или число появления события при нескольких испытаниях. Число возможных значений дискретной случайной величины может быть конечным или бесконечным (счётным множеством)

Для сравнения - непрерывная случайная величина может принимать любые значения из некоторого числового промежутка: например, температура воздуха в определённый день, вес ребёнка в каком-либо возрасте, и т.д.

Закон распределениядискретной случайной величины представляет собой перечень всех её возможных значений и соответствующих вероятностей. Сумма всех вероятностей Σp_i = 1. Закон распределения также может быть задан аналитически (формулой) и графически (многоугольником распределения, соединяющим точки (x_i; p_i)

Функция распределения случайной величины - это вероятность того, что случайная величина (назовём её ξ) примет значение меньшее, чем конкретное числовое значение x:F(X) = P(ξ < X).

Для дискретной случайной величины функция распределения вычисляется для каждого значения как сумма вероятностей, соответствующих всем предшествующим значениям случайной величины. Ниже будет приведён пример, разъясняющий смысл сказанного.