Б-8. Принцип практической невозможности маловероятных событий

При решении многих практических задач приходится иметь дело с событиями, вероятность которых весьма мала, г. е. близка к нулю. Можно ли считать, что маловероятное событие А в единичном испытании не произойдет? Такого заключения сделать нельзя, так как не исключено, хотя и мало вероятно, что событие А наступит.

Казалось бы, появление или непоявление маловероят­ного события в единичном испытании предсказать невоз­можно Однако длительный опыт показывает, что малове­роятное событие в единичном испытании в подавляющем большинстве случаев не наступает На основании этого (|>акта принимают следующий «принцип практической невозможности маловероятных событий»: если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это событие не наступит.

Естественно возникает вопрос: насколько малой должна быть вероятность события, чтобы можно было считать не­возможным его появление в, одном испытании? На этот вопрос нельзя ответить однозначно. Для задач, различных по существу, ответы будут разными. Например, если ве­роятность того, что парашют при прыжке не раскроется, р.шиа 0,01, то было бы недопустимым применять такие па­рашюты. Если же вероятность того, что поезд дальнего следования прибудет с опозданием, равна 0,01, то можно

практически быть уверенным, что поезд прибучет вовремя.

Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровней значимости. На практи­ке обычно принимают уровни значимости, заключенные между 0,01 ii 0,05. Уровень значимости, равный 0,01, на­зывают однопроцентным; уровень значимости, равный 0,02, называют двухпроцентным и г. д.

Подчеркнем, что рассмотренный здесь принцип поз­воляет делать предсказания не только о событиях, имею­щих малую вероятность, но и о событиях, вероятность ко­торых близка к единице. Действительно, если событие А имеет вероятность близкую к нулю, то вероятность проти­воположного события /4 близка к единице. С другой сто­роны, непоявление события А означает наступление проти­воположного события .1. Таким образом, нз принципа не­возможности маловероятных событии вытекает следующее важное для приложении следствие: если случайное событие имеет вероятность очень близкую к единице, то практи­чески можно считать, что в единичном испытании это событие наступит. Разумеется, н здесь ответ на вопрос о том, какую вероятность считать близкой к единице, зави­сит от существа задачи.

Б-9 Теоремы умножения вероятностей.

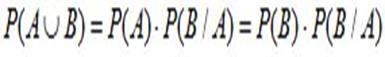ошибка-пересечение (2.9)

Вероятность произведения (пересечения, совмещения) двух событий равна вероятности одного из них, умноженной на условную вероятность второго при наличии первого(правило умножения вероятностей).

Правило умножения вероятностей может быть обобщено на случай произвольного числа событий

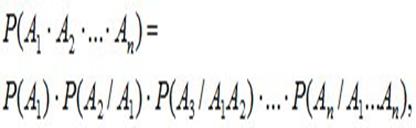(2.10)

т.е. вероятность произведения нескольких событий равна произведению вероятностей этих событий, причем вероятность каждого последующего события вычисляется при условии, что все предыдущие имели место.

Событие A называется независимымот события B, если его вероятность не зависит от того, произошло событие B или нет, т.е. P(B/A)=P(B).

Для независимых событий правило произведения вероятностей принимает вид:

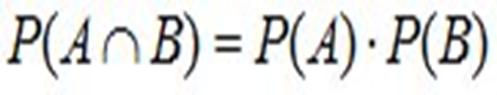.(2.11)

Несколько событий A₁, A₂, …, A_n называются независимыми, если любое из них не зависит от любой комбинации (произведения) любого числа других. Для независимых событий правило умножения принимает вид:

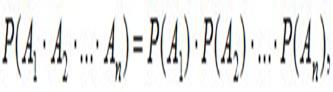(2.12)

или

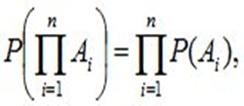(2.13)

т.е. вероятность произведения нескольких независимых событий равна произведению вероятностей этих событий.

Заметим, что если имеется несколько событий A₁, A₂, …, A_n, то их попарная независимость (т.е. независимость любых двух событий A_i и A_j, i≠j) еще не означает их независимости в совокупности.

Б-11Следствия из формулы Бернулли.

1. Вероятность того, что событие А наступит менее k раз

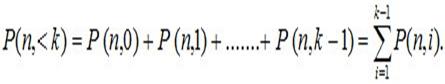(4.2)

2. Вероятность того, что событие наступит более k раз

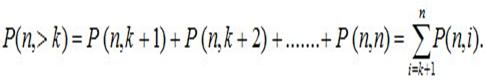(4.3)

3. Вероятность того, что в n опытах схемы Бернулли, событие А появится от k1 до k2 раз

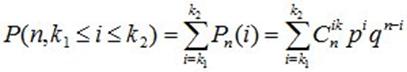. (4.4)

4. Вероятность того, что в n опытах событие А появится хотя бы один раз, определяется формулой

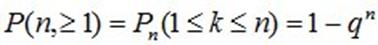(4.5)

Число к₀, которому соответствует максимальная биномиальная вероятность 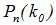, называется наивероятнейшим числом появления события А. При заданных n и p это число определяется неравенствами: .

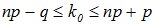Б-12 Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно, например, 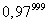вычислить трудно. В этом случае для вычисления вероятности того, что в n испытаниях (n – велико) событие произойдет k раз, используют формулу Пуассона:

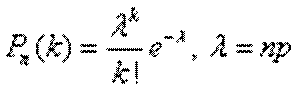– среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для 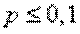и 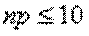. При больших 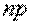рекомендуется применять формулы Лапласа (Муавра-Лапласа). Cобытия, для которых применима формула Пуассона, называют редкими, так как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).

Б-13

ТеоремаМуавра —Лапласа — одна из предельных теорем теории вероятностей, установлена Лапласом в 1812 году. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0<р<1) и m — число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа.

Рассмотрим задачу: монету подбрасывают 200 раз. Необходимо вычислить вероятность появления герба в 90 испытаниях. Применим формулу Бернулли:

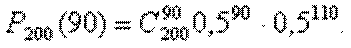
Видим, что вычислить по данной формуле требуемую вероятность довольно сложно из-за громоздких вычислений. Рассмотрим методы вычислений , дающие возможность с довольно высокой точностью найти вероятность в подобных случаях. Первый из них описан в теореме Муавра- Лапласа. Эта теорема дает приближенную формулу для вычисления вероятности появления события А в схеме повторных испытаний, когда нужно вычислить появление события А ровно т раз из п испытаний.

Теорема Муавра- Лапласа: Если вероятность наступления события А в каждом из п независимых испытаниях равна р и отлична от 0 и единицы, а число испытаний достаточно велико, то вероятность Р_п(т)того, что в п испытаниях событие А наступит т раз, приближенно равна значению функции

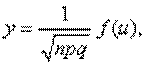
где

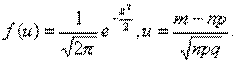
Б-14 Интегральная теорема Муавра- Лапласа: Если вероятность р наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность Р_п(т₁, т₂) того, что событие А появится в п испытаниях от т₁ до т₂ раз. Приближенно равна определенному интегралу

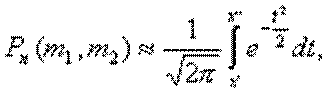где

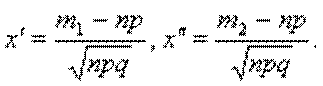
Данный интеграл называется функцией Лапласа и обозначается Ф(х).

Б-15 Следствия из интегральной теоремы Муавра—Лапласа (с выводом). Примеры.

Пусть выполнили условие применимости интегральной теоремы М.Лапласа, тогда: 1)Вероятность того, что число m наступлений события А в n испытаниях отличается от величины np не более, чем на эпсило (E) (по абсолютной величине) вычисл. по след. формуле:

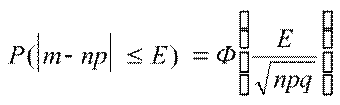
2)Вер-ть того что частость (доля) m/n наступлений событий А в n испытаниях отличается от вер-ти р не более чем на D (по абсолютной величине) вычисл. По след. формуле

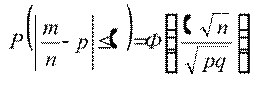
Б-16 Производящая функция последовательности f₀, f₁..., f_n... функция

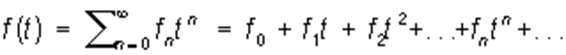
(в предположении, что этот степенной ряд сходится хотя бы для одного значения t ≠ 0). П. ф. называют также генератрисой. Последовательность f₀, f₁..., f_n... может быть как числовая, так и функциональная; в последнем случае П. ф. зависит не только от t, но и от аргументов функций f_n. Например, если f_n = aqⁿ где а и q — постоянные, то П. ф.

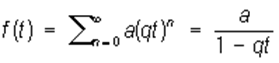
если f_n — Фибоначчи числа; f₀ = 0, f₁ = 1, f_n+2= f_n+1+ f_n, то П. ф.

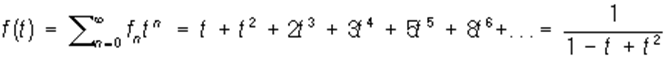
если f_n = Т _n(х) — Чебышева многочлены: T₀(х)= 1, T_n (х)= cos (n arc cos x), то П. ф.

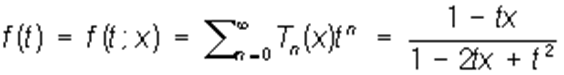
и т.д. Знание П. ф. последовательности часто облегчает изучение свойств последней. П. ф. применяются в теории вероятностей, в теории функций и в алгебре (в теории инвариантов). Впервые метод П. ф. был применен П. Лапласом для решения некоторых проблем теории вероятностей.