Группы нелинейных характеристик звеньев

К нелинейным автоматическим системам относятся системы, динамические свойства которых описываются нелинейными уравнениями.

К таким описаниям приводят нелинейные характеристики звеньев, образующих систему. Если уравнение хотя бы одного звена окажется нелинейным, то автоматическая система будет нелинейной.

Нелинейные характеристики звеньев условно можно разделить на следующие группы:

Первую группу составляют релейные звенья т.е. такие звенья у которых при непрерывном изменении входного сигнала 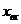выходной сигнал 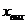изменяется скачком при определенных значениях входного сигнала, а между этими значениями остается постоянным (рис). Примерами таких звеньев могут служить различные типы реле и релейных усилителей.

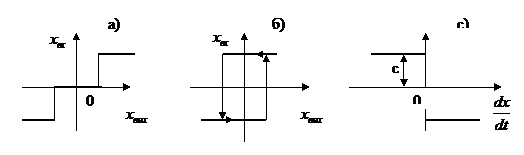
Вторая группа нелинейных характеристик относится к звеньям, у которых выходная величина 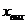является непрерывной кусочно-линейной функцией входной величины 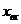, т.е. графически эта функция состоит из отрезков прямых линий. Звеном с такой характеристикой является гидравлический двигатель (включает гидравлический цилиндр 1 и управляющий золотник 2, рис.2). На этом же рисунке изображена характеристика двигателя, отражающая функциональную зависимость изменений выходной величины 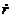- скорости движения штока поршня от изменения входной величины 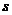- перемещения штока золотника. Видно, что графически эта функция состоит из отрезков прямых линий. На рисунке шток золотника находится в нейтральном положении 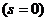. В этом случае поршень гидравлического двигателя находится в неподвижном состоянии 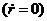. При смещении штока золотника 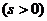рабочая жидкость от насоса под давлением поступает по отверстию, называемому в корпусе в полость, располагающую над поршнем или под ним. Отверстие имеет размер 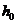и называется буксой. В результате, поршень гидравлического двигателя начинает перемещаться вверх или вниз со скоростью 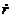, пропорциональной величине .

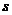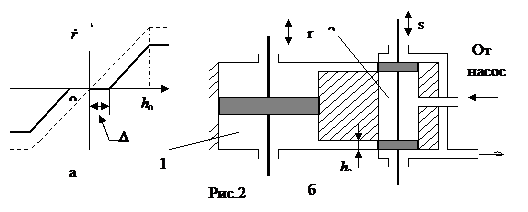
Скорость перемещения поршня будет увеличиваться по мере увеличения проходного сечения в буксе, рис.2а. После полного открытия буксы, дальнейшее увеличение скорости перемещения поршня двигателя прекратится. На рис.2а пунктирной линией показан график изменения скорости 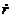. Видно, что при 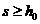скорость движения поршня не изменяется. Сплошной линией на рис.2а показан график изменения скорости 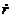, но для случая, когда ширина пояска поршня управляющего золотника 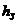, больше размера буксы, т.е. Δ 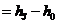. Видно, что при Δ > 0 появляется зона нечувствительности. Управляющий золотник, у которого 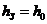называется проточным. Золотник называется отсечным, если .

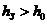Отмеченные особенности формируют кусочно-линейный характер зависимости изменения выходного и выходного сигналов.

Третий вид нелинейностей составляют звенья с криволинейными статическими характеристиками. Многие нелинейности такого вида могут быть линеаризованы с помощью разложения в ряд Тейлора. Такие нелинейности называют несущественными. Нелинейности, относящиеся к первым двум группам, называют существенными.

Существуют и др. типы нелинейностей. Обычно нелинейности рассматриваются как факторы, затрудняющие расчет систем управления. В этих случаях стремятся уменьшить количество нелинейностей. Но они могут и специально вводиться в систему для придания ей лучших свойств, например, трения - для достижения устойчивости.

28. Какой критерий применяется для определения частоты и амплитуды колебаний в нелинейных системах?

Применяется критерий устойчивости Михайлова. Предварительно выполняется линеаризация описания нелинейного звена. Далее получают линеаризованное описание системы

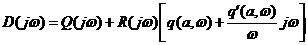, (1)

где 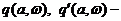коэффициенты гармонической линеаризации,

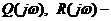полиномы при линейной и нелинейной частями описания системы.

Затем уравнение кривой Михайлова (1) представляется в виде суммы мнимой и вещественной частей

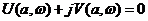
где U ( 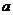, 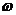) и V( 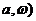- мнимая и вещественная части уравнения кривой Михайлова.

В соответствии с критерием условием возникновения автоколебаний является прохождение кривой через начало системы координат, см. рис.

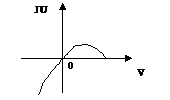
Это условие математически записывается так:

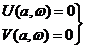
В результате решения системы находятся амплитуда 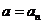и частота 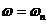автоколебаний