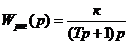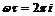Исходная предпосылка для линеаризации

Линеаризацией называется операция замены действительного нелинейного уравнения элемента приближенным линейным.

Линеаризация оказывается возможной, если выполняется исходная предпосылка.

Содержание предпосылки: в процессе функционирования элемента, уравнение которого линеаризуется, принадлежащие ему переменные должны изменяться так, чтобы ихотклонения от значений, соответствующих установившемуся режиму оставались все время достаточно малыми.

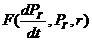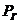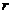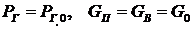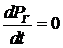Например, в нелинейном уравнении переменными являются давление газа в емкости и положение заслонки , регулирующей расход газа из емкости. На установившемся режиме: и . В соответствии с предпосылкой в окрестности установившегося режима отклонение Δ 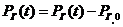должно быть мало. Также должно быть мало и отклонение Δ 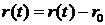, ( 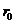- положение заслонки в установившемся режиме).

8. Уравнение движения

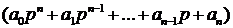
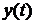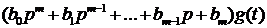= где 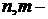степени старших производных левой и правой частей уравнения 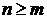; 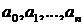и 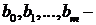постоянные коэффициенты.

Управляемость системы

Объект (или система) является полностью управляемой, если существует такое управляющее воздействие u(t), определенное на конечном интервале времени 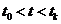, которое переводит его из любого начального состояния 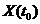в любое заданное конечное состояние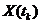

10.Трансцендентное звено. Характеристики

Звено «чистого» запаздывания. Уравнение для этого звена имеет вид

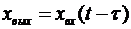, (1.67)

где 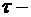величина «чистого» запаздывания, рис.1.30. Рисунок отражает принцип работы звена. Видно, что после подачи сигнала на вход звена, сигнал на его выходе возникает только в момент времени .

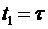Выражение для передаточной функции звена:

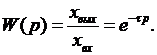(1.68)

Для определения частотных характеристик необходимо в выражении (1.68) выполнить замену 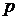на произведение 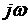. После замены получим

= .

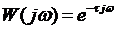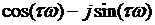Далее можно записать выражения для мнимой и вещественной частей частотной передаточной функции:

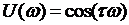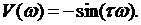, (1.69)

Из выражений (1.69) нетрудно найти амплитудную и фазовую частотные характеристики: ,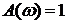

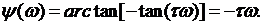
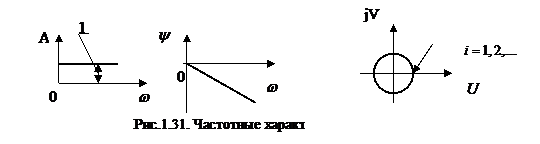
На рис.1.31. изображены амплитудная фазовая и амплитудно-фазовая частотные характеристики звена «чистого» запаздывания.

Примеры звеньев «чистого» запаздывания:

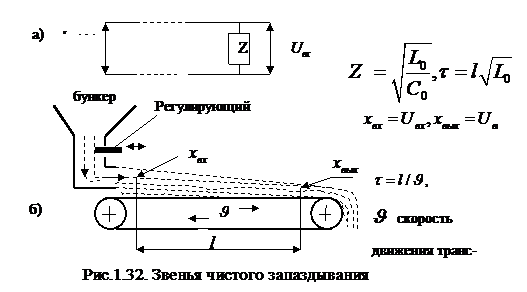
1.Электрическая линия без потерь, имеющая сопротивление 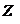при индуктивности 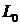и емкости 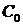на единицу длинны, рис.1.32,а

2.Транспортер сыпучих материалов, рис.1.32,б.

11. Корни характенистического уравнениямогут быть комплексные 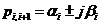и вещественные, В случае комплексных корней переходные процессы будут колебательными и сходящимися, если вещественная часть хотя бы одного комплексного корня меньше нуля 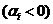и колебательными расходящимися, если вещественная часть комплексного корня больше нуля, см рис.

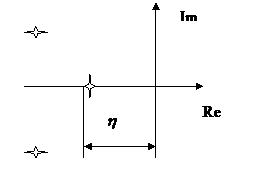
12. Все корнирасположенные слева от границы устойчивости соответствуют устойчивым системам, Если хотя бы один корень расположится справо от границы, система окажется неустойчивой. Если комплексные корни попадают на границу, то в системе будут автоколебания с постоянной амплитудой. Если вещественный корень попадает на границу, то процесс в системе не будет изменяться во времени.

Определитель Гурвица.

Для системы 3 порядка имеет вид

А1	А3
А0	А2
	А1	А3

14 Показатель затухания 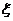для колебательного звена имеет вид

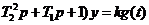( имеет вид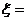 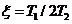С учетом этого описание звена примет вид .

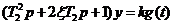Если 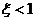то переходная характеристика у звена будет иметь вид колебательного процесса. Если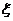 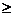1, то этот процесс будет апериодическим.. Если 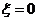, то процесс будет незатухающим с постоянной амплитудой

15. Если известна величина степени устойчивости 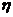,то время переходного процесса можно определить по формуле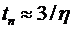

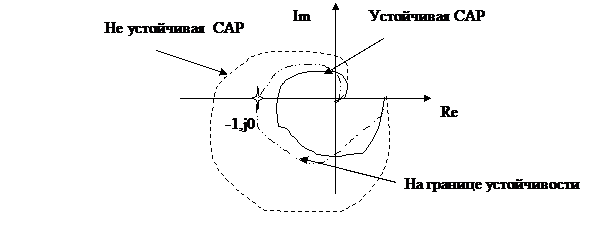
16. По критерию Найквиста система неустойчива если годограф амплитудно-частотной характеристики разомкнутой системы не охватывает точку с координатами (-1, j,0)

17. Регулятордолжен быть интегрирующим