Тема 9. Теория вероятностей. Числовые характеристики: математическое ожидание, дисперсия, среднеквадратическое отклонение
1. Какая числовая характеристика отражает среднее значение случайной величины или центр рассеивания случайной величины?
+a. математическое ожидание;
-b. дисперсия;
-c. корреляционный момент.
2. Какая числовая характеристика отражает рассеивание или разброс случайной величины относительно центра её рассеивания?
-a. математическое ожидание;
+b. дисперсия;
-c. корреляционный момент.
3. Какая числовая характеристика отражает зависимость случайных величин входящих в систему?
-a. математическое ожидание;
-b. дисперсия;
+c. корреляционный момент.
4. По цели производится три независимых выстрела. Вероятность попадания в цель при одном выстреле равна 0,3 и от выстрела к выстрелу не изменяется. Найти математическое ожидание случайной величины Х – числа попаданий в цель при трёх выстрелах.
+a. 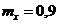 ;
;
-b. 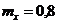 ;
;
-c. 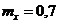 .
.
5. По цели производится три независимых выстрела. Вероятность получения недолёта равна 0,2 и от выстрела к выстрелу не изменяется. Найти математическое ожидание случайной величины Х – числа недолётов при трёх выстрелах. Вероятностью попадания в цель пренебречь.
-a. 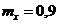 ;
;
-b. 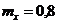 ;
;
+c. 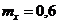 .
.
6. По цели производится три независимых выстрела. Вероятность попадания в цель при одном выстреле равна 0,4 и от выстрела к выстрелу не изменяется. Найти ряд математическое ожидание случайной величины Х – числа попаданий в цель при трёх выстрелах.
-a. 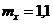 ;
;
+b. 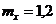 ;
;
-c. 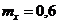 .
.
7. По цели производится три независимых выстрела. Вероятность получения недолёта равна 0,6 и от выстрела к выстрелу не изменяется. Найти математическое ожидание случайной величины Х – числа недолётов при трёх выстрелах. Вероятностью попадания в цель пренебречь.
+a. 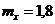 ;
;
-b. 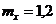 ;
;
-c. 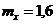 .
.
8. По цели производится три независимых выстрела. Вероятность попадания в цель при одном выстреле равна 0,7 и от выстрела к выстрелу не изменяется. Найти математическое ожидание случайной величины Х – числа попаданий в цель при трёх выстрелах.
-a. 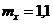 ;
;
+b. 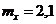 ;
;
-c. 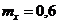 .
.
9. При стрельбе по цели расходуется 144 снаряда. Вероятность попадания в цель от выстрела к выстрелу не изменяется и равна 0,03. Используя предельное свойство биномиального распределения определить математическое ожидание случайной величины Х – числа попаданий в цель для Х = {0, 1, 2, 3, 144}.
-a. 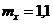 ;
;
-b. 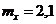 ;
;
+c. 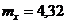 .
.
10. По цели производится стрельба снарядами с установкой на фугасное действие для получения рикошетов (воздушных разрывов). При стрельбе расходуется 120 снарядов. Вероятность получения наземного разрыва равна 0,05. Используя предельное свойство биномиального распределения определить математическое ожидание случайной величины Х – числа наземных разрывов для Х = {0, 1, 2, 120}.
-a. 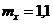 ;
;
+b. 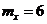 ;
;
-c. 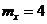 .
.
11. В магазин поступила партия лампочек в количестве 300 штук. Вероятность наличия бракованных лампочек в партии равна 0,01. Используя предельное свойство биномиального распределения определить математическое ожидание случайной величины Х – числа бракованных лампочек для Х = {0, 1, 2, 3, 300}.
+a. 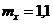 ;
;
-b. 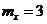 ;
;
-c. 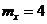 .
.
12. При стрельбе по цели расходуется 256 снарядов. Вероятность попадания в цель от выстрела к выстрелу не изменяется и равна 0,01. Используя предельное свойство биномиального распределения определить математическое ожидание случайной величины Х – числа попаданий в цель для Х = {0, 1, 2, 256}.
-a. 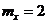 ;
;
-b. 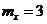 ;
;
+c. 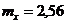 .
.
13. В магазин поступила партия лампочек в количестве 250 штук. Вероятность наличия бракованных лампочек в партии равна 0,02. Используя предельное свойство биномиального распределения определить математическое ожидание случайной величины Х – числа бракованных лампочек для Х = {0, 1, 2, 250}.
-a. 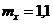 ;
;
+b. 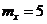 ;
;
-c. 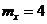 .
.
14. РЛС способна засечь цель в среднем за 2 минуты. Определить дисперсию случайной величины Х – числа целей, засеченных РЛС за 12 минут для Х = {0, 1, 2, 3}.
+a. а = 6;
-b. а = 3;
-c. а = 7.
