Схема системы управления с обратной связью

Любой объект, относящийся к классу организационно-экономических, является управляемой системой. Управление системой общепринято разделять на планирование, регулирование, учет, контроль, анализ. На рис. 1.3. представлена крайне упрощенная схема системы управления с обрат­ной связью, включающей сам объект управления, управляющий орган и информационную часть.

Пусть на входе системы (например, предприятия) лицом, ответст­венным за принятие решения, установлены план – желаемый результат ее функционирования – и ресурсы, обеспечивающие его реализацию. Действительный результат функционирования системы (продукция) измеряется информационной частью и сравнивается с планом. На основе анализа рассогласований управляющий орган (подразделения управле­ния на предприятии) вырабатывает регулирующие воздействия на объект управления (цехи предприятия) с целью уменьшения рассогласований.

Рис. 1.3. Упрощенная схема системы управления с обратной связью

Независимо от характера и специфики исследуемого объекта его цели всегда относятся к двум категориям: развития и стабилизации. Цели развитиянаправлены на достижение новых, желательных в ка­ком-то смысле состояний или характеристик объекта и соответствуют фазе управления “планирование” (рис. 1.3). Цели стабилизациинаправлены на сохранение или поддержание в определенном состоянии характе­ристик объекта и соответствуют фазе управления “регулирование”. Если рассматривать в качестве объекта исследования цех, то регули­рующие воздействия подразделений управления выступают для него в качестве основных плановых показателей и ресурсов цеха, обеспечи­вающих реализацию плана предприятия .

Таким образом, цели развития объекта вытекают из целей системы верхнего уровня или по крайней мере являются им логически непротиворечивыми. Поэтомукорректная постановка задач “на развитие” системы обязательно предусматривает рассмотрение целей системы верхнего уровня и ее возможностей, формализующих их критериев оценки и формирование на этой основе ограничений, накладываемых системой верхнего уровня на объект исследования. Однако такого рода анализ весьма трудоемок и не всегда осуществляется на практике, что зачастую приводит к недо­статочно обоснованным уровням ограничений.

Цели стабилизации в соответствии с вышесказанным способствуют достижению результатов целей развития (утвержденного плана) и опре­деляются на уровне исследуемой системы. При постановке задач на “стабилизацию” оценивается оптимальность лишь одной из подсистем исследуемой системы – управляющей, при этом основные параметры объекта, определяющие его состояние, получены из решения задачи на развитие (или каким-нибудь иным способом) и зафиксированы.

Качественными (точечными) называются цели, которые могут быть или достигнуты, или не достигнуты. Все результаты, приводящие к достижению цели, одинаково хороши, а все результаты, не приводящие к достижению цели, одинаково неудовлетворительны. Критерии оценки достижения подобных целей принимают только два значения: 1 – успех, 0 в противоположном случае. Чаше всего в модели подобные цели выступают в качестве ограничений.

Количественное (интервальное) определение цели заключается в стремлении увеличить (или уменьшить) значение некоторой величины – критерия оптимальности, зависимость которой от переменных и факторов модели и составляет целевую функцию математической модели. Здесь следует сделать следующее терминологическое замечание. В литературе по экономико-математическому моделированию широкое распространение получили термины “критерий эффективности” и “критерий оптимальности”. С точки зрения методологии моделирования смешивать эти термины неправомерно. Как уже было отмечено выше, оптимальное решение – это решение математической модели, наилучшее по некоторому показателю – критерию оптимальности. Но математическая модель лишь отражение действительности, построенное на основе учета основных количественных факторов. Действительность богаче модели в первую очередь за счет присутствия качественных факторов, не формализуемых моделью. Эффективное решение предполагает обяза­тельный учет неформализуемых факторов, в связи с чем критерий эффективности математической модели в принципе не существует. Обычно эффективное решение явно или неявно заменяется оптимальным. Спецификой оптимальности является ее жесткая связь с критерием оптимальности, чего нет у эффективности. Критерий оптимальности при этом некоторая величина, имеющая экономический смысл. Наилучшее по критерию оптимальности решение вовсе не обязано совпадать с эффективным. Особенно ясно это видно при принятии решений в условиях многокритериальности – ведь критериев несколько, несколько оптимальных решений, а эффективное решение только одно. Эффективизация, базируясь и включая оптимизацию, в значительной мере носит эвристический характер из-за наличия неформализуемой информации. Таким образом, количественная цель формализуется критерием опти­мальности, а не критерием эффективности.

Критерии оптимальности

Основная проблема постановки экстремальных задач заключается в формулировке целевой функции. Сложность выбора целевой функции состоит в том, что любой технический, организационно-экономический объект первоначально имеет векторный характер критериев оптимальности (многокритериальность), причем улучшение одного из выходных параметров, как правило, приводит к ухудшению другого, так как все выходные параметры являются функциями одних и тех же управляемых параметров и не могут изменяться независимо друг от друга. Такие выходные параметры называют конфликтными параметрами. Задачи проектирования, проводимые по нескольким критериям оптимизации, носят название задач векторной оптимизации.

Целевая функция должна быть одна (принцип однозначности). Сведение многокритериальной задачи к однокритериальной называют сверткой векторного критерия. Задача поиска его экстремума сводится к задаче математического программирования. В зависимости от того, каким образом выбираются и объединяются выходные параметры в скалярной функции качества, различают частные, аддитивные, критерий формы функции, мультипликативные, минимаксные, и т.д.

Частные критерии могут применяться в случаях, когда среди выходных параметров можно выделить один основной параметр у_i(X), наиболее полно отражающий эффективность проектируемого объекта. Этот параметр принимают за целевую функцию. Примерами таких параметров являются: для энергетического объекта – мощность, для технологического автомата – производительность, для транспортного средства – грузоподъемность. Для многих технических объектов таким параметром служит стоимость. Условия работоспособности всех остальных выходных параметров объекта относят при этом к функциональным ограничениям. Оптимизация на основе такой постановки называется оптимизацией по частному критерию.

Достоинство такого подхода – его простота, существенный недостаток – то, что большой запас работоспособности можно получить только по основному параметру, который принят в качестве целевой функции, а другие выходные параметры вообще не будут иметь запасов.

Взвешенный аддитивный критерий применяют тогда, когда условия работоспособности позволяют выделить две группы выходных параметров. В первую группу входят выходные параметры, значения которых в процессе оптимизации нужно увеличивать 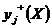(производительность, качество, вероятность безотказной работы изделий и т.п.), во вторую — выходные параметры, значения которых следует уменьшать 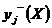(расход энергоресурсов, трудоемкость производства изделий и пр.). Объединение нескольких выходных параметров, имеющих в общем случае различную физическую размерность, в одной скалярной целевой функции требует предварительного нормирования этих параметров.

Нормированные критерии представляют собой отношение «натурального» частного критерия к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам критерий. При этом выбор нормирующего делителя должен быть логически обоснован.

Первый подход предлагает принимать в качестве нормирующего делителя директивные значения параметров, заданные заказчиком в техническом задании. Необходимо учитывать, что в ТЗ на проектируемый объект могут быть заданы оптимальные значения параметров.

Второй подход предполагает выбор в качестве нормирующих делителей максимальных значений критериев, достигаемых в области существования проектных решений (в области компромисса). Возможен вариант, при котором в качестве нормирующих делителей выбирают разность между максимальным и минимальным значениями критерия в области компромисса.

Выбор подхода к формированию безразмерной формы частных критериев в значительной степени носит субъективный характер и должен обосновываться в каждом конкретном случае.

Пусть при проектировании некоторого объекта существует n частных критериев. Тогда целевая функция задачи оптимизации при применении аддитивного критерия имеет вид

, (1.1)

где c_i – весовой коэффициентi-го частного критерия; F_i⁰ – i –й нормирующий делитель; f_i(Х)– нормированное значение i-го частного критерия.

Функция (1.1) позволяет осуществлять компромисс, при котором улучшение значения одного нормированного частного критерия компенсирует ухудшение значений других.

Введение весовых коэффициентов должно учитывать различную значимость частных критериев при формировании аддитивного критерия. Определение весовых коэффициентов сталкивается с серьезными трудностями и обычно сводится к использованию формальных процедур, либо к применению экспертных оценок.

С появлением обобщенного критерия исчезают логические проблемы, связанные с установлением взаимосвязей между частными критериями различной размерности и выбором наилучшего варианта проектируемого объекта, и остаются лишь вычислительные трудности.

Аддитивный критерий имеет ряд недостатков:

· не являясь объективным в части функционирования объекта или системы, он выступает как формальный математический прием, придающей задаче удобный для решения вид;

· при использовании его может происходить взаимная компенсация частных критериев, которая позволяет уменьшение одного из критериев вплоть до нулевого значения компенсировать возрастанием другого. Поэтому необходимо вводить ограничения на минимальные значения частных критериев и их весовых коэффициентов.

Несмотря на недостатки, обобщенный аддитивный критерий позволяет решать успешно многокритериальные задачи и получать полезные результаты.

Критерий формы функции используют, когда ставится задача наилучшего совпадения заданной (эталонной) характеристики 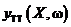с соответствующей выходной характеристикой 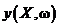проектируемого объекта, где ω – некоторая переменная, например, стоимость, качество.

Мультипликативные критерии. Аддитивные критерии основаны на использовании принципа компенсации абсолютных значений нормированных частных критериев. Но в ряде случаев более целесообразным является оперирование не с абсолютными, а с относительными изменениями значений частных критериев.

Разделим выходные параметры объекта на три группы по типу соответствующих им условий работоспособности.

К первой группе отнесем параметры 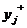, имеющие условия работоспособности вида

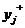>TT_j, (1.14)

т.е. параметры, для которых желательно максимальное увеличение.

Ко второй группе отнесем параметры 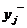с условиями работоспособности

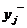<TT_j. (1.15)

Для этих параметров желательна минимизация.

Третья группа будет образована параметрами 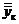с условиями работоспособности типа равенств

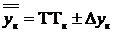(1.16)

где ТТ_к– заданные технологические требования; 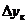– максимально допустимое по ТЗ отклонение 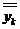от ТТ_к

Мультипликативные критерии могут применяться в тех случаях, когда в ТЗ отсутствуют условия работоспособности типа равенства и выходные параметры не могут принимать нулевые значения. Тогда целевая функция, подлежащая максимизации, имеет вид

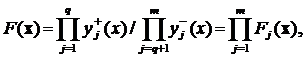(1.17)

где в числителе перемножаются все выходные параметры с условиями работоспособности (1.14), а в знаменателе фигурируют все параметры с условиями работоспособности типа (1.15).

Мультипликативный критерий образуется путем простого перемножения частных критериев в том случае, если все они имеют одинаковую важность. В случае неравноценности частных критериев вводятся весовые коэффициенты c_i и мультипликативный критерий принимает вид

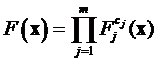
Удобство этого критерия в том, что выходные параметры не требуют какого-либо нормирования. Однако последнее приводит к следующему серьезному недостатку: критерий компенсирует недостаточную величину одного частного критерия избыточной величиной другого и имеет тенденцию сглаживать уровни частных критериев за счет неравнозначных первоначальных значений частных критериев.

Например, заданы условия работоспособности у₁ > 9 и у₂ > 9, причем у₁ и у₂ – конфликтные параметры и у₁(х)и у₂(х) таковы, что имеются точки х_а и х_б , в которых у₁(х_а) = 10, у₂(х_а) = 10, у₁(х_б) = 13, у₂(х_б) = 8. Тогда с позицией мультипликативного критерия точка х_б лучше, так как здесь f(х_б) = 13∙8 = 104>f(х_a) = 10∙10 = 100. Однако это противоречит смыслу ТЗ, так как в точке х_а требования ТЗ выполнены, а в точке х_б – нет. Этот недостаток связан с неучетом в мультипликативном критерии технических требований на выходные параметры, зафиксированных в ТЗ.

Минимаксные (максиминные) критерии. В теории векторной оптимизации особое место занимает принцип компромисса, основанный на идее равномерности. На базе этого принципа работают все минимаксные (максиминные) критерии.

Сущность принципа максимина заключается в следующем. При проектировании сложных технических объектов при наличии большого числа частных критериев довольно трудно, а зачастую и невозможно установить аналитическую взаимосвязь между критериями. Поэтому, основываясь на идее равномерного компромисса, стараются найти такие значения переменных проектирования Х, при которых нормированные значения всех частных критериев становятся равными между собой.

При большом числе частных критериев из-за сложных взаимосвязей очень трудно добиться равенства частных критериев. В этом случае оказывается полезным применение принципа максимина, заключающегося в такой вариации значений переменных проектирования Х, при которой последовательно «подтягиваются» те нормированные критерии, численные значения которых в исходном решении оказались наименьшими. Вследствие того, что операции производятся в области компромисса, подтягивание «отстающего» критерия неизбежно приводит к снижению значений части остальных критериев. Но при проведении ряда шагов можно добиться определенной степени уравнивания противоречивых (конфликтных) частных критериев, что и является целью принципа максимина.

Пусть условия работоспособности всех выходных параметров приведены к виду (1.15). Такое преобразование в отношении условий (1.14) было пояснено выше, а условие (1.16) преобразуются в (1.15) путем записи следующих неравенств: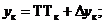

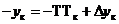
Если обозначить у_к1= - у_к, то вместо условия работоспособности типа равенства одного параметра получим два эквивалентных ему условия работоспособности типа неравенства для параметров у_к и у_к1 . Введем количественную оценку степени выполнения j-ой работоспособности и обозначим ее S_j. Цели расчета совпадают с целями увеличения S_j (причем в первую очередь тех из S_j, которые являются наименьшими). Отсюда приходим к целевой функции вида

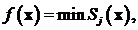j 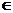=[1:m]. (1.18)

где m – количество условий работоспособности после их приведения к виду (1.15). Функцию (1.18) называют функцией минимума, и поскольку требуется ее максимизация, т.е. maxminS_j(x), x 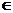D, j 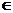=[1:m], то критерий с целевой функцией (1.17) называется максиминным критерием. Если бы требовалось минимизировать функцию максимума, то получился бы минимаксный критерий.

В максимином критерии нет того главного недостатка, который был присущ мультипликативному и аддитивному критериям. Здесь влияние на целевую функцию оказывает только тот выходной параметр, который в данной точке x является наихудшим с позиций выполнения требований технического задания.

Выбор критерия оптимальности является сложной методологической проблемой и, как правило, может производиться неоднозначно. Источником сложности этой проблемы, прежде всего, служит противоречивость целей, преследуемых при проектировании любого нового технического объекта. Стоимость и надежность функционирования, энергоемкость, производительность и массогабаритные параметры всегда находились и будут находиться в противоречии друг с другом.

Если в ТЗ на проектирование сформулировано, что требуется оптимизировать один из параметров проектируемого объекта при соблюдении ограничительных требований на остальные параметры, то необходимо сформировать частный критерий. В этих случаях задача оптимального проектирования сводится к задаче оптимизации с учетом заданных ограничений, т.е. к задаче условной оптимизации.

При наличии нескольких критериев оптимальности аддитивный критерий выбирают тогда, когда существенное значение имеют абсолютные значения критериев при выбранном векторе параметров проектирования Х.

Если существенную роль играет изменение абсолютных значений частных критериев при вариации вектора переменных Х, то в этом случае целесообразно применять мультипликативный критерий оптимальности.

Если перед проектировщиком стоит задача достижения равенства нормированных значений конфликтных частных критериев, то оптимальное проектирование следует проводить по минимаксному критерию.