Системный и функциональный подход
При проектировании сложных технических систем должен соблюдаться системный подход. В нем выделяют следующие принципы:
· иерархичность – каждая подсистема или элемент может рассматриваться как система;
· структурность – возможность описания системы с помощью коммутационных связей между ее элементами;
· взаимозависимость – проявление свойств системы только при взаимодействии с окружающей средой;
· множественность описания – описание системы на основе множества математических моделей;
· целостность изучаемой системы – изучение свойств целостной системы на основе анализа и знаний частей этого целого.
В основе системного подхода лежит исследование объекта как системы, направленное на поиск механизмов целостности объектов и выявление всех его связей. Системный подход требует очень широкого фронта работ, больших финансовых затрат, которые обычно не под силу одному предприятию.
Системный подход обосновывает общую оптимизацию проектирования, конструирования, производства, эксплуатации объекта. Одна из важнейших задач системного подхода – выбор вида, числа, уровня сложности, формы представления математических моделей. В общем случае системный подход при проектировании – это учет всех факторов, которые влияют на процесс создания объекта. Другими словами, системный подход – это решение технической задачи для части с учетом целого.
Поэтому часто пользуются функциональным подходом, при котором обычно проводят глубокую разработку отдельных наиболее важных систем с последующим внедрением их на предприятии.
Недостатком функционального подхода является то, что отдельно созданные системы обычно с большим трудом стыкуются между собой и требуют подчас взаимной доработки, например, по информационному обеспечению, т.к. появляется вероятность нежелательного параллелизма и дублирования инормации во входных и выходных документах. Выходом из положения является предварительное согласование систем по информационному обеспечению на стадии технического задания или технического проекта. Такое соглсование позволяет создать информационно-поисковую систему (ИПС).
Таким образом, современный переход к созданию сложных технических систем требует использования современных ЭВМ, обладающих хорошим быстродействием, большой памятью и развитым математическим обеспечением, обязательного наличия в своем составе ИПС, основанной на единстве информационного обеспечения между различными подсистемами, унифицированной технологии и типизации решений при разработке алгоритмов, иерархического принципа построения алгоритмов (рис. 1.2).
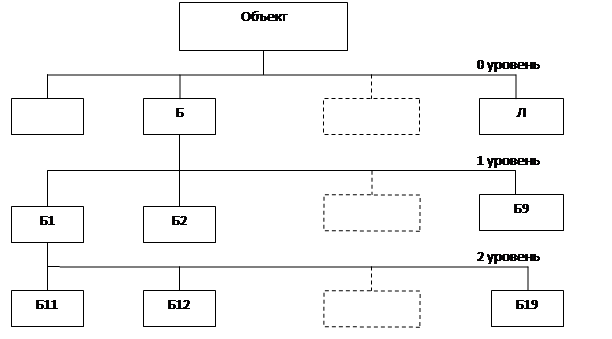
Рис. 1.2. Иерархический принцип построения сложных технических систем
Основные блоки макросхемы соответствуют нулевому уровню иерархии и оформляются в виде основных программ. Каждый блок, в свою очередь, делится на новые блоки, образующие более низкий уровень иерархии (1-й уровень). Они представляют собой решение более мелкой, но законченной задачи. Таким образом, для каждого блока нулевого уровня может быть составлена макросхема 1-го уровня иерархии и т.д. Деление обычно выполняют так, чтобы число блоков не превышало 9 и его целесообразно заканчивать на 3-4 уровнях. Задачи на последнем уровне нерационально дробить на новые блоки, так как они представляют собой последовательность элементарных действий, которые более удобно выражать при помощи макросхемы.
Иерархический принцип построения сложных технических систем предполагает модульный принцип построения программ.
Модульная структура программы разрабатывается на стадии технического проекта. Результатом проектирования модульной структуры является определение состава программных модулей и установление связей между ними по управлению и данным.
Требования к математическим моделям
Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, универсальности, робастности, продуктивности, наглядности и экономичности.
В общем случае под адекватностью понимают степень соответствия модели тому реальному явлению или объекту, для описания которого она строится. Модель считается адекватной,если отражает заданные свойства объекта с приемлемой точностью. Точность определяется как степень совпадения значений выходных параметров модели и объекта.
Чтобы уменьшить влияние неопределенности целесообразно проводить сравнение моделей по результатам их использования в некоторых стандартных ситуациях. Отражающих характерные особенности функционирования объектов на практике и называемых тестовыми ситуациями.
Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. Если задаться предельной допустимой погрешностью Епред, то можно в пространстве внешних параметров выделить область, в которой выполняется условие
Ем< Епред (1.13)
где Ем – погрешность модели.
Эту область называют областью адекватности (ОА) модели. Определение областей адекватности для конкретных моделей – сложная процедура, требующая больших вычислительных затрат. Эти затраты и трудности представления ОА быстро растут с увеличением размерности пространства внешних параметров. Пример ОА (заштриховано) в двумерном пространстве дан на рис. 1.10.


Рис. 1.10. Пример области адекватности
Здесь qk – k-й внешний параметр.
Расчет областей адекватности становится оправданным в связи с однократностью определения ОА и многократностью их использования при проектировании. Знание ОА позволяет правильно выбирать модели элементов из числа имеющихся и тем самым повышать достоверность результатов машинных расчетов.
Оценка адекватности может быть основана на сравнении измерений реальной системы и результатов экспериментов на модели:
· по средним значениям откликов модели и системы;
· по дисперсиям отклонений откликов модели от среднего значения откликов системы;
· по максимальному значению относительных отклонений откликов модели от откликов системы.
Универсальность. При определении ОА необходимо выбрать совокупность внешних параметров и совокупность выходных уi, отражающих учитываемые в модели свойства. Типичными внешними параметрами при этом являются параметры нагрузки и внешних воздействий для изделий (электрических, механических, тепловых, радиационных и т.п.), для предприятий – стоимость сырья, энергоносителей, комплектующих и пр. Увеличение числа учитываемых внешних факторов расширяет применимость модели, но существенно удорожает работу по определению ОА.
Степень универсальности математических моделей определяется их применимостью к анализу определенной группы однотипных объектов, к их анализу в одном или многих режимов функционирования и соответствует полноте учета в них свойств реальных задач. Если адекватность характеризуется положением и размерами ОА, то универсальность модели определяется числом и составом учитываемых в модели внешних и выходных параметров. Усложняя модель, т.е. увеличивая степень ее универсальности можно увеличивать приближение математической модели к реальной задаче.
Робастность математических моделей (ММ) (от англ. слова robust – крепкий, устойчивый) характеризует ее устойчивость по отношению к погрешностям исходных данных, способность нивелировать эти погрешности и не допускать их чрезмерного влияния на результат вычислительного эксперимента. Причинами низкой робастности ММ могут быть необходимость при ее количественном анализе вычитания близких друг к другу приближенных значений величин или деления на малую по модулю величину.
В теории моделирования понятие устойчивости включает – способность модели сохранять адекватность при исследовании эффективности системы на всем возможном диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы. Универсальной процедуры проверки устойчивости модели не существует.
Устойчивость результатов моделирования может быть оценена методами математической статистики. Как известно, основная задача математической статистики заключается в проверке выдвинутой гипотезы относительно свойств некоторого множества элементов, называемого генеральной совокупностью, и полученной из последней выборки.
Оценка чувствительности. Устойчивость является положительным свойством модели. Однако если изменение входных воздействий или параметров модели (в некотором заданном диапазоне) не отражается на значениях выходных параметров, то польза от такой модели невелика (ее иногда называют «бесчувственной»). В связи с этим возникает задача оценивания чувствительности модели к изменению параметров рабочей нагрузки и внутренних параметров самой системы. Такую оценку проводят по каждому параметру Xk в отдельности.
Основана она на том, что обычно диапазон возможных изменений параметра известен. Одна из наиболее простых и распространенных процедур оценивания состоит в следующем:
1) вычисляется величина относительного среднего приращения параметра Xk:
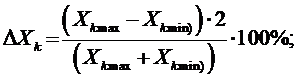
2) проводится пара модельных экспериментов при значениях Xk = Xkmax и Xk = Xkmin и средних фиксированных значениях остальных параметров. Определяются значения отклика модели Y1 = f(Xkmax) и Y2 = f(Xkmin);
3) вычисляется ее относительное приращение наблюдаемой переменной Y:
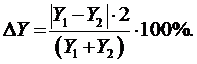
В результате для k-го параметра модели имеют пару значений (∆Xk, ∆Yk), характеризующую чувствительность модели по этому параметру. Аналогично формируются пары для остальных параметров модели, которые образуют множество (∆Xk, ∆Yk).
Данные, полученные при оценке чувствительности модели, могут быть использованы, в частности, при планировании экспериментов: большее внимание должно уделяться тем параметрам, по которым модель является более чувствительной.
Калибровка модели. Если в результате проведенной оценки качества модели оказалось, что ее целевые свойства не удовлетворяют разработчика, необходимо выполнить ее калибровку, т.е. коррекцию с целью приведения в соответствие предъявляемым требованиям.
Процесс калибровки носит итеративный характер и состоит из трех основных этапов:
1) глобальные изменения модели (например, введение новых процессов, изменение типов событий и т.п.);
2) локальные изменения модели (в частности, изменение некоторых законов распределения моделируемых случайных величин);
3) изменение специальных параметров, называемых калибровочными.
Попытка откалибровать модель путем изменения параметров и локальных модификаций могут оказаться безуспешными, хотя они и менее затратные по времени, но лучше начинать калибровку с внесения глобальных изменений.
Все же целесообразнее объединить оценку целевых свойств имитационной модели и ее калибровку в единый процесс. В этом случае процедура калибровки состоит из трех шагов, каждый из которых является итеративным.
Шаг 1. Сравнение выходных распределений. Цель – оценка адекватности модели. Критерии сравнения могут быть различными. Устранение различий на этом шаге основано на внесении глобальных изменений.
Шаг 2. Балансировка модели. Основная задача – оценка устойчивости и чувствительности модели. По его результатам, как правило, производятся локальные изменения (но возможны и глобальные).
Шаг 3. Оптимизация модели. Цель этапа – обеспечение требуемой точности результатов. Здесь возможны три основных направления работ:
· дополнительная проверка качества датчиков случайных чисел;
· снижение влияния переходного режима;
· применение специальных методов понижения дисперсии.
Продуктивность ММ связана с возможностью располагать достаточно достоверными исходными данными. Если они являются результатом измерений, то точность их измерения должна быть выше, чем для тех параметров, которые получаются при использовании ММ. В противном случае ММ будет непродуктивной и ее применение для анализа конкретного технического объекта теряет смысл.
Наглядность является ее желательным, но необязательным свойством.
Экономичность математических моделей (в частности, и машинных расчетных методов) оценивается прежде всего затратами машинного времени Тм и объемом используемой памяти
Vм = Vоп +Vвн,
где Vоп – объем оперативной памяти; Vвн – объем внешней памяти. Учитывая, что Vвн ≥ Vоп, то при анализе затрат памяти в большинстве случаев оценку можно вести по Vвн.
Машинное время дорого, поэтому его затраты определяют главную часть стоимостных затрат. Чем меньше Тм и Vм, тем математическая модель считается экономичнее. Величину Тм определяют как усредненное число операций Nоп, выполняемых при однократном обращении к модели. Величину Vм определяют, в основном, числом В внутренних параметров, используемых в математической модели. Чем больше таких параметров, тем больше затраты машинной памяти, тем больше усилий требуется для получения сведений о числовых значениях параметров и их разбросе. Сравнение математических моделей по экономичности состоит в сравнении значений Nоп и В.
