Экономико-математическая модель

Понятие моделирования

Моделирование– это изучение реальной системы (оригинала) путем замещения ее новым объектом (моделью), имеющим с ней определенные объектные соответствия и позволяющим прогнозировать ее функциональные особенности.

Процесс моделирования включает несколько этапов:

1 этап.Постановка задачи и определение свойств реального объекта, подлежащих исследованию.

2 этап.Констатация затруднительности или невозможности исследования реального объекта.

3 этап. Выбор модели, хорошо фиксирующей основные свойства объекта с одной стороны и легко поддающейся исследованию с другой. Модель должна отражать основные свойства объекта и не должна быть громоздкой.

4 этап.Исследование модели в соответствии с поставленной целью (проведение экспериментов).

5 этап. Проверка адекватности объекта и модели. Если нет соответствия, то необходимо повторить первые четыре этапа .

6 этап. Окончательный выбор модели.

Таким образом, моделирование состоит в выявлении основных свойств исследуемого процесса, построении моделей и их применении для прогнозирования поведения натуры. Критерием правильности моделирования является практика.

При машинном моделировании динамические характеристики, интересующие исследователя, легко и быстро воспроизводятся на экране дисплея. Этот вид моделирования часто называют численным экспериментом.

Поэтому термин моделирование отражает и интерактивную форму связи человека с вычислительной машиной.

Цели моделирования:

· обоснование достоверности математических описаний;

· получение функциональных связей между величинами;

· сравнение конечного числа стратегий решения индивидуальной проблемы, т.е. ответ на вопросы: что будет, если...?;

· идентификация моделируемой системы;

· оптимизация модели. Выбор целевых функций;

· применение моделирования для обучения и тренировки.

Оригинал – объект, определенные свойства которого подлежат изучению методом моделирования. Здесь необходимо обострить внимание на том, что все практические исследования имеют определенную направленность, при этом изучаются определенные свойства объекта, поэтому модель копирует оригинал не полностью, а частично с необходимой для проведения исследования точностью.

Поэтому при создании модели следует выделять существенные и не существенные свойства, которые требуется моделировать, например, при исследовании движения маятника, образованного тяжелым грузом, подвешенным на конце нити, существенным является то, что колебания маятника носят регулярный характер, а несущественным обстоятельство - то, что нить белая, а груз черный.

Оригиналом может быть как реально существующие, так и проектируемые объекты (системы, подсистемы, элементы, а также явления и процессы, происходящие в них).

Оригинал – замещаемый (моделируемый) объект.

Модель – это вспомогательный объект позволяющий отображать, оценивать, рассчитывать и замещать оригинал.

В общем случае модель – это явление, техническое устройство, знаковое образование, которые находятся в определенном соответствии с изучаемым объектом - оригиналом и способны замещать оригинал в процессе исследования, давая о нем необходимую информацию.

Модель всегда проще натуры, т.е. точных моделей натуры принципиально быть не может.

При использовании метода моделирования свойства и поведение объекта изучают путем применения вспомогательной системы (модели), находящейся в определенном объективном соответствии с исследуемым объектом.

Под объектом исследования понимается либо некоторая система, элементы которой в процессе достижения конечной цели реализуют один или несколько процессов, либо некоторый процесс, реализуемый элемен­тами одной или нескольких систем. В связи с этим в дальнейшем тексте термины “модель объекта”, “модель системы”, “модель процесса” сле­дует воспринимать как эквивалентные.

Представления о тех или иных свойствах объектов, их взаимосвязях формируются исследователем в виде описаний этих объектов на обыч­ном языке, в виде рисунков, графиков, формул или реализуются в виде макетов и других устройств. Подобные способы описания обобщаются в едином понятии – модель. Модели позволяют вынести упрощенное представление о системе и получить некоторые результаты намного проще, чем при изу­чении реального объекта. Более того, гипотетические модели объекта могут быть исследованы и изучены перед тем, как объект будет создан.

В практике исследования производственно-экономических объектов модели могут применяться для самых разных целей, что вызывает использование моделей различных классов. Построение одной-единственной математической модели для сложной производственной систе­мы практически не представляется возможным без разработки вспомо­гательных моделей. Поэтому, как правило, при создании конечной математической модели исследуемого объекта строят частные вспомо­гательные модели, отражающие ту или иную информацию об объекте, имеющуюся у разработчика на данном этапе построения модели.

Различают следующие модели.

Физическиемодели подразделяются на модели подобия и аналоговые. Модели подобия характеризуются некоторыми масштабными изменениями, выбираемыми в соответствии с критериями подобия (например, глобус - модель Земного шара). Аналоговые модели основаны на известных аналогиях между протеканием процессов в механических, тепловых, электриче­ских, и других динамических системах и предназначены для исследования статических и динамических свойств объекта (например, изучение колебаний пружинного маятника на моде­ли, реализуемой электрическим колебательным контуром).

Символическиемодели характерны тем, что параметры реального объекта и отношения между ними представлены символами: семантическими (словами), математическими, логическими. Наряду со словесными описаниями функциони­рования объектов - сценариями - сюда также относятся схематические модели: чертежи, графики и блок-схемы, логические блок-схемы (напри­мер, алгоритмы программ) и таблицы решений, кривые, таблицы и номограммы, а также математические описания - математические модели.

Среди смешанныхмоделей особое значение в экономической прак­тике имеют человеко-машинные модели (программа, реализующая на ЭВМ некоторую математическую модель, плюс человек, принимающий решение за счет обмена информацией с моделью).

Форма модели определяет и метод работы с ней. При исследовании различного рода объектов применяются три вида моделирования:

физическое, когда модель воспроизводит изучаемый процесс (ориги­нал) с сохранением его физической природы (продувка модели самолета в аэродинамической трубе);

аналоговое, основанное на известных аналогиях между протеканием механических, тепловых, электрических, ядерных и других динамиче­ских процессов (изучение свойств колебаний пружинного маятника на модели электрического колебательного контура представляет собой аналоговое моделирование с использованием принципов прямой ана­логии);

математическое, в основе которого лежит исследование математи­ческого описания (математической модели) изучаемого объекта.

Целевое назначение модели. По целевому назначению модели подраз­деляются на модели структуры, функционирования и стоимостные (модели расхода ресурсов).

Требования к математическим моделям

Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, универсальности, робастности, продуктивности, наглядности и экономичности.

В общем случае под адекватностью понимают степень соответствия модели тому реальному явлению или объекту, для описания которого она строится. Модель считается адекватной,если отражает заданные свойства объекта с приемлемой точностью. Точность определяется как степень совпадения значений выходных параметров модели и объекта.

Чтобы уменьшить влияние неопределенности целесообразно проводить сравнение моделей по результатам их использования в некоторых стандартных ситуациях. Отражающих характерные особенности функционирования объектов на практике и называемых тестовыми ситуациями.

Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. Если задаться предельной допустимой погрешностью Е_пред, то можно в пространстве внешних параметров выделить область, в которой выполняется условие

Е_м< Е_пред (1.13)

где Е_м – погрешность модели.

Эту область называют областью адекватности (ОА) модели. Определение областей адекватности для конкретных моделей – сложная процедура, требующая больших вычислительных затрат. Эти затраты и трудности представления ОА быстро растут с увеличением размерности пространства внешних параметров. Пример ОА (заштриховано) в двумерном пространстве дан на рис. 1.10.

Рис. 1.10. Пример области адекватности

Здесь q_k – k-й внешний параметр.

Расчет областей адекватности становится оправданным в связи с однократностью определения ОА и многократностью их использования при проектировании. Знание ОА позволяет правильно выбирать модели элементов из числа имеющихся и тем самым повышать достоверность результатов машинных расчетов.

Оценка адекватности может быть основана на сравнении измерений реальной системы и результатов экспериментов на модели:

· по средним значениям откликов модели и системы;

· по дисперсиям отклонений откликов модели от среднего значения откликов системы;

· по максимальному значению относительных отклонений откликов модели от откликов системы.

Универсальность. При определении ОА необходимо выбрать совокупность внешних параметров и совокупность выходных у_i, отражающих учитываемые в модели свойства. Типичными внешними параметрами при этом являются параметры нагрузки и внешних воздействий для изделий (электрических, механических, тепловых, радиационных и т.п.), для предприятий – стоимость сырья, энергоносителей, комплектующих и пр. Увеличение числа учитываемых внешних факторов расширяет применимость модели, но существенно удорожает работу по определению ОА.

Степень универсальности математических моделей определяется их применимостью к анализу определенной группы однотипных объектов, к их анализу в одном или многих режимов функционирования и соответствует полноте учета в них свойств реальных задач. Если адекватность характеризуется положением и размерами ОА, то универсальность модели определяется числом и составом учитываемых в модели внешних и выходных параметров. Усложняя модель, т.е. увеличивая степень ее универсальности можно увеличивать приближение математической модели к реальной задаче.

Робастность математических моделей (ММ) (от англ. слова robust – крепкий, устойчивый) характеризует ее устойчивость по отношению к погрешностям исходных данных, способность нивелировать эти погрешности и не допускать их чрезмерного влияния на результат вычислительного эксперимента. Причинами низкой робастности ММ могут быть необходимость при ее количественном анализе вычитания близких друг к другу приближенных значений величин или деления на малую по модулю величину.

В теории моделирования понятие устойчивости включает – способность модели сохранять адекватность при исследовании эффективности системы на всем возможном диапазоне рабочей нагрузки, а также при внесении изменений в конфигурацию системы. Универсальной процедуры проверки устойчивости модели не существует.

Устойчивость результатов моделирования может быть оценена методами математической статистики. Как известно, основная задача математической статистики заключается в проверке выдвинутой гипотезы относительно свойств некоторого множества элементов, называемого генеральной совокупностью, и полученной из последней выборки.

Оценка чувствительности. Устойчивость является положительным свойством модели. Однако если изменение входных воздействий или параметров модели (в некотором заданном диапазоне) не отражается на значениях выходных параметров, то польза от такой модели невелика (ее иногда называют «бесчувственной»). В связи с этим возникает задача оценивания чувствительности модели к изменению параметров рабочей нагрузки и внутренних параметров самой системы. Такую оценку проводят по каждому параметру X_k в отдельности.

Основана она на том, что обычно диапазон возможных изменений параметра известен. Одна из наиболее простых и распространенных процедур оценивания состоит в следующем:

1) вычисляется величина относительного среднего приращения параметра X_k:

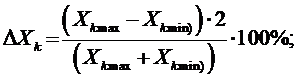
2) проводится пара модельных экспериментов при значениях X_k = X_kmax и X_k = X_kmin и средних фиксированных значениях остальных параметров. Определяются значения отклика модели Y₁ = f(X_kmax) и Y₂ = f(X_kmin);

3) вычисляется ее относительное приращение наблюдаемой переменной Y:

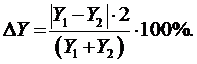
В результате для k-го параметра модели имеют пару значений (∆X_k, ∆Y_k), характеризующую чувствительность модели по этому параметру. Аналогично формируются пары для остальных параметров модели, которые образуют множество (∆X_k, ∆Y_k).

Данные, полученные при оценке чувствительности модели, могут быть использованы, в частности, при планировании экспериментов: большее внимание должно уделяться тем параметрам, по которым модель является более чувствительной.

Калибровка модели. Если в результате проведенной оценки качества модели оказалось, что ее целевые свойства не удовлетворяют разработчика, необходимо выполнить ее калибровку, т.е. коррекцию с целью приведения в соответствие предъявляемым требованиям.

Процесс калибровки носит итеративный характер и состоит из трех основных этапов:

1) глобальные изменения модели (например, введение новых процессов, изменение типов событий и т.п.);

2) локальные изменения модели (в частности, изменение некоторых законов распределения моделируемых случайных величин);

3) изменение специальных параметров, называемых калибровочными.

Попытка откалибровать модель путем изменения параметров и локальных модификаций могут оказаться безуспешными, хотя они и менее затратные по времени, но лучше начинать калибровку с внесения глобальных изменений.

Все же целесообразнее объединить оценку целевых свойств имитационной модели и ее калибровку в единый процесс. В этом случае процедура калибровки состоит из трех шагов, каждый из которых является итеративным.

Шаг 1. Сравнение выходных распределений. Цель – оценка адекватности модели. Критерии сравнения могут быть различными. Устранение различий на этом шаге основано на внесении глобальных изменений.

Шаг 2. Балансировка модели. Основная задача – оценка устойчивости и чувствительности модели. По его результатам, как правило, производятся локальные изменения (но возможны и глобальные).

Шаг 3. Оптимизация модели. Цель этапа – обеспечение требуемой точности результатов. Здесь возможны три основных направления работ:

· дополнительная проверка качества датчиков случайных чисел;

· снижение влияния переходного режима;

· применение специальных методов понижения дисперсии.

Продуктивность ММ связана с возможностью располагать достаточно достоверными исходными данными. Если они являются результатом измерений, то точность их измерения должна быть выше, чем для тех параметров, которые получаются при использовании ММ. В противном случае ММ будет непродуктивной и ее применение для анализа конкретного технического объекта теряет смысл.

Наглядность является ее желательным, но необязательным свойством.

Экономичность математических моделей (в частности, и машинных расчетных методов) оценивается прежде всего затратами машинного времени Т_м и объемом используемой памяти

V_м = V_оп +V_вн,

где V_оп – объем оперативной памяти; V_вн – объем внешней памяти. Учитывая, что V_вн ≥ V_оп, то при анализе затрат памяти в большинстве случаев оценку можно вести по V_вн.

Машинное время дорого, поэтому его затраты определяют главную часть стоимостных затрат. Чем меньше Т_м и V_м, тем математическая модель считается экономичнее. Величину Т_м определяют как усредненное число операций N_оп, выполняемых при однократном обращении к модели. Величину V_м определяют, в основном, числом В внутренних параметров, используемых в математической модели. Чем больше таких параметров, тем больше затраты машинной памяти, тем больше усилий требуется для получения сведений о числовых значениях параметров и их разбросе. Сравнение математических моделей по экономичности состоит в сравнении значений N_оп и В.

Критерии оптимальности

Основная проблема постановки экстремальных задач заключается в формулировке целевой функции. Сложность выбора целевой функции состоит в том, что любой технический, организационно-экономический объект первоначально имеет векторный характер критериев оптимальности (многокритериальность), причем улучшение одного из выходных параметров, как правило, приводит к ухудшению другого, так как все выходные параметры являются функциями одних и тех же управляемых параметров и не могут изменяться независимо друг от друга. Такие выходные параметры называют конфликтными параметрами. Задачи проектирования, проводимые по нескольким критериям оптимизации, носят название задач векторной оптимизации.

Целевая функция должна быть одна (принцип однозначности). Сведение многокритериальной задачи к однокритериальной называют сверткой векторного критерия. Задача поиска его экстремума сводится к задаче математического программирования. В зависимости от того, каким образом выбираются и объединяются выходные параметры в скалярной функции качества, различают частные, аддитивные, критерий формы функции, мультипликативные, минимаксные, и т.д.

Частные критерии могут применяться в случаях, когда среди выходных параметров можно выделить один основной параметр у_i(X), наиболее полно отражающий эффективность проектируемого объекта. Этот параметр принимают за целевую функцию. Примерами таких параметров являются: для энергетического объекта – мощность, для технологического автомата – производительность, для транспортного средства – грузоподъемность. Для многих технических объектов таким параметром служит стоимость. Условия работоспособности всех остальных выходных параметров объекта относят при этом к функциональным ограничениям. Оптимизация на основе такой постановки называется оптимизацией по частному критерию.

Достоинство такого подхода – его простота, существенный недостаток – то, что большой запас работоспособности можно получить только по основному параметру, который принят в качестве целевой функции, а другие выходные параметры вообще не будут иметь запасов.

Взвешенный аддитивный критерий применяют тогда, когда условия работоспособности позволяют выделить две группы выходных параметров. В первую группу входят выходные параметры, значения которых в процессе оптимизации нужно увеличивать 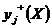(производительность, качество, вероятность безотказной работы изделий и т.п.), во вторую — выходные параметры, значения которых следует уменьшать 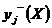(расход энергоресурсов, трудоемкость производства изделий и пр.). Объединение нескольких выходных параметров, имеющих в общем случае различную физическую размерность, в одной скалярной целевой функции требует предварительного нормирования этих параметров.

Нормированные критерии представляют собой отношение «натурального» частного критерия к некоторой нормирующей величине, измеряемой в тех же единицах, что и сам критерий. При этом выбор нормирующего делителя должен быть логически обоснован.

Первый подход предлагает принимать в качестве нормирующего делителя директивные значения параметров, заданные заказчиком в техническом задании. Необходимо учитывать, что в ТЗ на проектируемый объект могут быть заданы оптимальные значения параметров.

Второй подход предполагает выбор в качестве нормирующих делителей максимальных значений критериев, достигаемых в области существования проектных решений (в области компромисса). Возможен вариант, при котором в качестве нормирующих делителей выбирают разность между максимальным и минимальным значениями критерия в области компромисса.

Выбор подхода к формированию безразмерной формы частных критериев в значительной степени носит субъективный характер и должен обосновываться в каждом конкретном случае.

Пусть при проектировании некоторого объекта существует n частных критериев. Тогда целевая функция задачи оптимизации при применении аддитивного критерия имеет вид

, (1.1)

где c_i – весовой коэффициентi-го частного критерия; F_i⁰ – i –й нормирующий делитель; f_i(Х)– нормированное значение i-го частного критерия.

Функция (1.1) позволяет осуществлять компромисс, при котором улучшение значения одного нормированного частного критерия компенсирует ухудшение значений других.

Введение весовых коэффициентов должно учитывать различную значимость частных критериев при формировании аддитивного критерия. Определение весовых коэффициентов сталкивается с серьезными трудностями и обычно сводится к использованию формальных процедур, либо к применению экспертных оценок.

С появлением обобщенного критерия исчезают логические проблемы, связанные с установлением взаимосвязей между частными критериями различной размерности и выбором наилучшего варианта проектируемого объекта, и остаются лишь вычислительные трудности.

Аддитивный критерий имеет ряд недостатков:

· не являясь объективным в части функционирования объекта или системы, он выступает как формальный математический прием, придающей задаче удобный для решения вид;

· при использовании его может происходить взаимная компенсация частных критериев, которая позволяет уменьшение одного из критериев вплоть до нулевого значения компенсировать возрастанием другого. Поэтому необходимо вводить ограничения на минимальные значения частных критериев и их весовых коэффициентов.

Несмотря на недостатки, обобщенный аддитивный критерий позволяет решать успешно многокритериальные задачи и получать полезные результаты.

Критерий формы функции используют, когда ставится задача наилучшего совпадения заданной (эталонной) характеристики 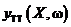с соответствующей выходной характеристикой 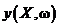проектируемого объекта, где ω – некоторая переменная, например, стоимость, качество.

Мультипликативные критерии. Аддитивные критерии основаны на использовании принципа компенсации абсолютных значений нормированных частных критериев. Но в ряде случаев более целесообразным является оперирование не с абсолютными, а с относительными изменениями значений частных критериев.

Разделим выходные параметры объекта на три группы по типу соответствующих им условий работоспособности.

К первой группе отнесем параметры 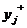, имеющие условия работоспособности вида

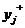>TT_j, (1.14)

т.е. параметры, для которых желательно максимальное увеличение.

Ко второй группе отнесем параметры 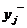с условиями работоспособности

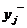<TT_j. (1.15)

Для этих параметров желательна минимизация.

Третья группа будет образована параметрами 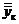с условиями работоспособности типа равенств

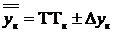(1.16)

где ТТ_к– заданные технологические требования; 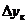– максимально допустимое по ТЗ отклонение 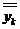от ТТ_к

Мультипликативные критерии могут применяться в тех случаях, когда в ТЗ отсутствуют условия работоспособности типа равенства и выходные параметры не могут принимать нулевые значения. Тогда целевая функция, подлежащая максимизации, имеет вид

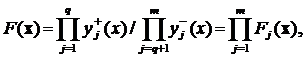(1.17)

где в числителе перемножаются все выходные параметры с условиями работоспособности (1.14), а в знаменателе фигурируют все параметры с условиями работоспособности типа (1.15).

Мультипликативный критерий образуется путем простого перемножения частных критериев в том случае, если все они имеют одинаковую важность. В случае неравноценности частных критериев вводятся весовые коэффициенты c_i и мультипликативный критерий принимает вид

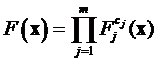
Удобство этого критерия в том, что выходные параметры не требуют какого-либо нормирования. Однако последнее приводит к следующему серьезному недостатку: критерий компенсирует недостаточную величину одного частного критерия избыточной величиной другого и имеет тенденцию сглаживать уровни частных критериев за счет неравнозначных первоначальных значений частных критериев.

Например, заданы условия работоспособности у₁ > 9 и у₂ > 9, причем у₁ и у₂ – конфликтные параметры и у₁(х)и у₂(х) таковы, что имеются точки х_а и х_б , в которых у₁(х_а) = 10, у₂(х_а) = 10, у₁(х_б) = 13, у₂(х_б) = 8. Тогда с позицией мультипликативного критерия точка х_б лучше, так как здесь f(х_б) = 13∙8 = 104>f(х_a) = 10∙10 = 100. Однако это противоречит смыслу ТЗ, так как в точке х_а требования ТЗ выполнены, а в точке х_б – нет. Этот недостаток связан с неучетом в мультипликативном критерии технических требований на выходные параметры, зафиксированных в ТЗ.

Минимаксные (максиминные) критерии. В теории векторной оптимизации особое место занимает принцип компромисса, основанный на идее равномерности. На базе этого принципа работают все минимаксные (максиминные) критерии.

Сущность принципа максимина заключается в следующем. При проектировании сложных технических объектов при наличии большого числа частных критериев довольно трудно, а зачастую и невозможно установить аналитическую взаимосвязь между критериями. Поэтому, основываясь на идее равномерного компромисса, стараются найти такие значения переменных проектирования Х, при которых нормированные значения всех частных критериев становятся равными между собой.

При большом числе частных критериев из-за сложных взаимосвязей очень трудно добиться равенства частных критериев. В этом случае оказывается полезным применение принципа максимина, заключающегося в такой вариации значений переменных проектирования Х, при которой последовательно «подтягиваются» те нормированные критерии, численные значения которых в исходном решении оказались наименьшими. Вследствие того, что операции производятся в области компромисса, подтягивание «отстающего» критерия неизбежно приводит к снижению значений части остальных критериев. Но при проведении ряда шагов можно добиться определенной степени уравнивания противоречивых (конфликтных) частных критериев, что и является целью принципа максимина.

Пусть условия работоспособности всех выходных параметров приведены к виду (1.15). Такое преобразование в отношении условий (1.14) было пояснено выше, а условие (1.16) преобразуются в (1.15) путем записи следующих неравенств: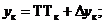

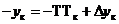
Если обозначить у_к1= - у_к, то вместо условия работоспособности типа равенства одного параметра получим два эквивалентных ему условия работоспособности типа неравенства для параметров у_к и у_к1 . Введем количественную оценку степени выполнения j-ой работоспособности и обозначим ее S_j. Цели расчета совпадают с целями увеличения S_j (причем в первую очередь тех из S_j, которые являются наименьшими). Отсюда приходим к целевой функции вида

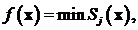j 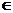=[1:m]. (1.18)

где m – количество условий работоспособности после их приведения к виду (1.15). Функцию (1.18) называют функцией минимума, и поскольку требуется ее максимизация, т.е. maxminS_j(x), x 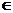D, j 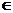=[1:m], то критерий с целевой функцией (1.17) называется максиминным критерием. Если бы требовалось минимизировать функцию максимума, то получился бы минимаксный критерий.

В максимином критерии нет того главного недостатка, который был присущ мультипликативному и аддитивному критериям. Здесь влияние на целевую функцию оказывает только тот выходной параметр, который в данной точке x является наихудшим с позиций выполнения требований технического задания.

Выбор критерия оптимальности является сложной методологической проблемой и, как правило, может производиться неоднозначно. Источником сложности этой проблемы, прежде всего, служит противоречивость целей, преследуемых при проектировании любого нового технического объекта. Стоимость и надежность функционирования, энергоемкость, производительность и массогабаритные параметры всегда находились и будут находиться в противоречии друг с другом.

Если в ТЗ на проектирование сформулировано, что требуется оптимизировать один из параметров проектируемого объекта при соблюдении ограничительных требований на остальные параметры, то необходимо сформировать частный критерий. В этих случаях задача оптимального проектирования сводится к задаче оптимизации с учетом заданных ограничений, т.е. к задаче условной оптимизации.

При наличии нескольких критериев оптимальности аддитивный критерий выбирают тогда, когда существенное значение имеют абсолютные значения критериев при выбранном векторе параметров проектирования Х.

Если существенную роль играет изменение абсолютных значений частных критериев при вариации вектора переменных Х, то в этом случае целесообразно применять мультипликативный критерий оптимальности.

Если перед проектировщиком стоит задача достижения равенства нормированных значений конфликтных частных критериев, то оптимальное проектирование следует проводить по минимаксному критерию.

Понятие моделирования

Моделирование– это изучение реальной системы (оригинала) путем замещения ее новым объектом (моделью), имеющим с ней определенные объектные соответствия и позволяющим прогнозировать ее функциональные особенности.

Процесс моделирования включает несколько этапов:

1 этап.Постановка задачи и определение свойств реального объекта, подлежащих исследованию.

2 этап.Констатация затруднительности или невозможности исследования реального объекта.

3 этап. Выбор модели, хорошо фиксирующей основные свойства объекта с одной стороны и легко поддающейся исследованию с другой. Модель должна отражать основные свойства объекта и не должна быть громоздкой.

4 этап.Исследование модели в соответствии с поставленной целью (проведение экспериментов).

5 этап. Проверка адекватности объекта и модели. Если нет соответствия, то необходимо повторить первые четыре этапа .

6 этап. Окончательный выбор модели.

Таким образом, моделирование состоит в выявлении основных свойств исследуемого процесса, построении моделей и их применении для прогнозирования поведения натуры. Критерием правильности моделирования является практика.

При машинном моделировании динамические характеристики, интересующие исследователя, легко и быстро воспроизводятся на экране дисплея. Этот вид моделирования часто называют численным экспериментом.

Поэтому термин моделирование отражает и интерактивную форму связи человека с вычислительной машиной.

Цели моделирования:

· обоснование достоверности математических описаний;

· получение функциональных связей между величинами;

· сравнение конечного числа стратегий решения индивидуальной проблемы, т.е. ответ на вопросы: что будет, если...?;

· идентификация моделируемой системы;

· оптимизация модели. Выбор целевых функций;

· применение моделирования для обучения и тренировки.

Оригинал – объект, определенные свойства которого подлежат изучению методом моделирования. Здесь необходимо обострить внимание на том, что все практические исследования имеют определенную направленность, при этом изучаются определенные свойства объекта, поэтому модель копирует оригинал не полностью, а частично с необходимой для проведения исследования точностью.

Поэтому при создании модели следует выделять существенные и не существенные свойства, которые требуется моделировать, например, при исследовании движения маятника, образованного тяжелым грузом, подвешенным на конце нити, существенным является то, что колебания маятника носят регулярный характер, а несущественным обстоятельство - то, что нить белая, а груз черный.

Оригиналом может быть как реально существующие, так и проектируемые объекты (системы, подсистемы, элементы, а также явления и процессы, происходящие в них).

Оригинал – замещаемый (моделируемый) объект.

Модель – это вспомогательный объект позволяющий отображать, оценивать, рассчитывать и замещать оригинал.

В общем случае модель – это явление, техническое устройство, знаковое образование, которые находятся в определенном соответствии с изучаемым объектом - оригиналом и способны замещать оригинал в процессе исследования, давая о нем необходимую информацию.

Модель всегда проще натуры, т.е. точных моделей натуры принципиально быть не может.

При использовании метода моделирования свойства и поведение объекта изучают путем применения вспомогательной системы (модели), находящейся в определенном объективном соответствии с исследуемым объектом.

Под объектом исследования понимается либо некоторая система, элементы которой в процессе достижения конечной цели реализуют один или несколько процессов, либо некоторый процесс, реализуемый элемен­тами одной или нескольких систем. В связи с этим в дальнейшем тексте термины “модель объекта”, “модель системы”, “модель процесса” сле­дует воспринимать как эквивалентные.