Тема 1. Системный подход и моделирование
Я.Д.Гельруд
МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ
Учебно-методический комплекс
Челябинск
УДК 510(022)(075.8)
Гельруд Я.Д. Методы принятия решений: Учебно-методический комплекс учебное пособие. – Челябинск: Изд. ЮУрГУ, 2005. –88 с.
Учебно-методический комплекс (УМК) по дисциплине «Методы принятия решений» предназначен для студентов, обучающихся по специальности 080507 "Менеджмент организации". УМК включает: рабочую программу дисциплины, календарно-тематический план для самостоятельной работы студентов, методические указания по самостоятельному изучению дисциплины, теоретический материал, практикум, содержащий примеры решения типовых задач, задания для контрольной работы по каждой теме и список общедоступной учебной и справочной литературы.
Теоретический материал представляет собой конспект лекций, содержит необходимые утверждения и алгоритмы принятия решений, при этом подробно демонстрируется применение рассматриваемого инструментария для решения конкретных управленческих задач. В силу этого данный УМК может быть использован при изучении данной дисциплины студентами, обучающимися по экономическим специальностям, с одной стороны, как справочное пособие, и, с другой стороны, как перечень необходимого объема алгоритмических и инструментальных средств, обеспечивающих принятие оптимальных решений в сложных управленческих ситуациях.
Рецензенты: уч. секретарь кафедры ЮУрГУ «Прикладная математика»
к.т.н., доцент Брагина А.А.; заведующий кафедрой ЮУрГУ
«Предпринимательство и менеджмент» к.т.н., профессор Горбунов Н.И.
© Гельруд Я.Д., 2005.
© Издательство , 2005.
СОДЕРЖАНИЕ
| Предисловие………………………………………………………....…….. | |
| Рабочая программа дисциплины……………………………………….. | |
| Календарно-тематический план работы студента………...…………. | |
| Методические рекомендации…………………………………………… | |
| Методические рекомендации по изучению теоретического материала | |
| Методические рекомендации по решению практических задач ………. | |
| Методические рекомендации по выполнению контрольных работ.….. | |
| Требования к оформлению практических заданий, контрольных работ и критерии их оценки………………………………………………………….. | |
| Теоретический материал по темам……………………………….…….. | |
| Тема 1. Системный подход и моделирование | |
| 1.1. Понятие системного подхода. | |
| 1.2. Общие понятия математического моделирования. | |
| 1.3. Декомпозиция управленческого решения. | |
| Тема 2. Правила принятия решений в условиях риска и неопределенности | |
| 2.1. Правила принятия решений без использования численных значений вероятностей исходов (критерий Сэвиджа, Вальда, Лапласа)……………… | |
| 2.2. Критерий Гурвица – компромиссный способ принятия решений……... | |
| 2.3. Правила принятия решений с использованием численных значений вероятностей исходов………………………………………………. | |
| 2.4. Зависимость решения от изменений значений вероятностей…………... | |
| 2.5. Стоимость достоверной информации……………………………………. | |
| 2.6. Использование математического ожидания и среднего квадратичного отклонения для оценки риска…………………………………………………. | |
| 2.7. Использование понятия полезности при определении размеров риска |
| Тема 3. Дерево решений | |
| 3.1. Некоторые задачи принятия решений и примеры использования | |
| деревьев решений……………………………………………………………… | |
| 3.2. Анализ чувствительности решений……………………………………… | |
| 3.3. Парадокс Алле…………………………………………………………... | |
| 3.4. Нерациональное поведение………………………………………………. | |
| Тема 4. Многокритериальные решения | |
| 4.1. Понятие многокритериальности………………………………………….. | |
| 4.2. Оптимальность по Парето………………………………………………… | |
| 4.3. Точки равновесия………………………………………………………….. | |
| Тема 5. Управление организационными системами | |
| 5.1. Распределение ресурсов…………………………………………………... | |
| 5.2. Управление посредством экспертного опроса………………………….. | |
| Тема 6. Коллективные решения | |
| 6.1. Парадокс Кондорсе……………………………………………………….. | |
| 6.2. Метод Борда………………………………………………………………. | |
| 6.3. Аксиомы Эрроу……………………………………………………………. | |
| 6.4. Принятие коллективных решений в малых группах……………………. | |
| Практикум…………………………………………………………………. | |
| Контрольные задания……………………………………………………. | |
| Предметный указатель……………………………………………….……. | |
| Рекомендуемая литература……………………………………………… |
ПРЕДИСЛОВИЕ
Методы решения задач организационного управления имеют общие основные методологические принципы, главными из которых являются системный подход и математическое моделирование (называемое также исследование операций). При весьма существенной общности этих принципов, не углубляясь в детали и строгость определений, отметим основные различия этих понятий, что необходимо для их правильного применения.
Первое. Исследование операций исходит из того, что цель и показатель оценки качества (критерий) способа достижения цели заданы. Задача исследования – найти лучший (в смысле заданного критерия) способ достижения заданной цели.
Системный анализ ориентирован на определение целей (целеположение) и критериев оценки способов их достижений и уже затем на поиск наилучшего способа (если выбрана неправильная цель, то есть опасность найти решение не той проблемы; получение точного ответа на неправильный вопрос менее полезно, чем не до конца точный ответ на правильный вопрос).
Таким образом, системный анализ в большей степени ориентирован на решение задач стратегического характера (стратегического планирования), а исследование операций – тактического (текущего планирования).
Второе. Исследование операций преимущественно ориентированно на принятие решений в условиях определенности исходных данных или, по выражению Е.С.Вентцель[2], в условиях
«доброкачественной» неопределенности, когда некоторые факторы,
влияющие на решение, представляют собой случайные величины,
статистические характеристики которых нам известны или могут быть изучены.
Системный анализ содержит методологические подходы и средства решения задач в условиях «недоброкачественной» неопределенности, когда ряд факторов неопределен и их статистические характеристики неизвестны.
Третье. Методология системного анализа включает методы и средства решения проблем и для тех ситуаций, когда ряд факторов (например, цель или критерий оценки и др.) в принципе не могут быть определены в виде численных величин, в то время как исследование операций ориентированно в основном на количественные методы принятия решений.
Некоторые отличительные особенности исследования операций и системного анализа приведены здесь с единственной целью – объяснить, как определен тот набор математических моделей и методов, который выделен для включения в настоящий курс. Представленные здесь модели и методы ориентированны на задачи, которые попадают в сферу как исследования операций, так и системного анализа.
Основные методы исследования операций включены в программу дисциплины “Математика” (4 семестр), кроме того, методы решения задач в условиях неполной или неопределенной информации опираются на раздел математики “Теория вероятностей и математическая статистика” (3 семестр), поэтому, приступая к изучению настоящей дисциплины, следует повторить указанные разделы “Математики”.
В настоящий курс наряду с описанием основных понятий системного анализа и методов математического моделирования (тема 1), включены методы принятия решений в стохастических условиях (темы 2, 3), в условиях многокритериальности (тема 4), а также специфические методы управления большими организационными системами (темы 5, 6).
РАБОЧАЯ ПРОГРАММА ДИСЦИПЛИНЫ
Тема 3. Дерево решений
Некоторые задачи принятия решений и примеры использования деревьев решений. Анализ чувствительности решений. Парадокс Алле. Нерациональное поведение.
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Методические рекомендации по изучению теоретического материала.
Теоретический материал представляет собой конспект лекций, содержащий необходимый набор утверждений и формул (без детальных подробностей их вывода и доказательств соответствующих теорем), но с подробным обоснованием их использования при решении конкретных управленческих задач. Необходимо тщательно разобрать все примеры, приведенные в каждой теме теоретических материалов, а также примеры в рекомендованных учебниках, и выполнить предлагаемые в них упражнения. Обратите внимание на стиль решения примеров – основные идеи решения обосновываются ссылкой на использованные утверждения, приводятся номера соответствующих формул. Подобный стиль должен быть Вами использован при выполнении практических заданий и контрольных работ. Для более глубокого понимания изучаемого методологического и инструментального аппарата следует воспользоваться общедоступными работами по методам принятия решений, перечень которых приведен в разделе «Рекомендуемая литература».
Методические рекомендации по решению практических задач.
Основная цель раздела «Практикум» – получение практических навыков решения конкретных задач и примеров по основным темам дисциплины. Решение предлагаемых в «Практикуме» заданий является средством текущего контроля приобретенных в течение семестра при самостоятельной работе знаний и навыков студентов, а также необходимо для самооценки студентами их подготовленности по каждой теме. По каждой теме необходимо решить (и предъявить для проверки) все предлагаемые примеры.
Изложение решения задач должно быть кратким, не загромождено текстовыми формулировками используемых утверждений и определений; простые преобразования и арифметические выкладки пояснять не следует. Степень подробности изложения решений задач должна соответствовать степени подробности решения примеров в соответствующих разделах теоретических материалов. Ключевые идеи решения следует обосновывать ссылкой на использованные утверждения и приводить номера соответствующих формул.
Методические рекомендации по выполнению контрольной работы.
Контрольная работа является важной частью итогового контроля зна- ний и навыков студентов по всем темам дисциплины. При выполнении работы студент учится работать со специальной литературой, обрабатывать полученную информацию, творчески ее использовать.
В контрольной работе должны быть выполнены все примеры раздела
«Контрольные задания».
Также как и при выполнении практических заданий, изложение решений контрольной работы должно быть кратким, не загромождено текстовыми формулировками используемых утверждений и определений; простые преобразования и арифметические выкладки пояснять не следует. Степень подробности изложения решений контрольной работы должна соответствовать степени подробности решения примеров в соответствующих разделах теоретических материалов. Ключевые идеи решения следует обосновывать ссылкой на использованные утверждения и приводить номера соответствующих формул.
Требования к оформлению практических заданий, контрольных работ и критерии их оценки.
Практические задания являются средством текущего контроля приобретенных в течение семестра знаний и навыков студентов, и выполняются по завершению изучения каждой темы (за исключением темы 1. Понятия этой темы являются базовыми и используются во всех последующих темах). Оценка выполнения практического задания проводится по 30-бальной системе (10 баллов на каждую задачу). 25-30 баллов, набранных студентом, соответствуют оценке "отлично", 20-24 балла – оценке "хорошо", 16-19 балла – оценке "удовлетворительно", 0-15 балла – оценке "неудовлетворительно".
В случае если задача решена в целом правильно, но допущены 1-2 арифметические ошибки, либо не объяснен какой-либо ключевой момент решения, решение оценивается в 8-10 баллов. Если решение задачи не доведено до конца, либо окончание решения ошибочно, но имеется правильный план решения и получены существенные, важные для решения результаты, задача оценивается в 4-8 баллов. Если задача не решена, отсутствует общий план решения либо допущены грубые ошибки, но есть продвижения в нужном направлении или правильно сделаны отдельные шаги решения, задача оценивается в 1-4 балла.
Оформление практической работы следующее: на титульной странице название дисциплины, название и номер темы, фамилия, имя, отчество
студента, факультет, номер группы и рамка для оценки заданий вида
| ∑ | |||
В остальном оформление свободное.
Контрольная работа предназначена для итогового контроля знаний и навыков студентов по всем темам за семестр. В отличие от практических заданий, оценка за каждую задачу контрольной работы - зачтено или не
зачтено.
Оценка зачтено ставится за правильное и полное решение задачи, допускаются небольшие погрешности в изложении и вычислениях. Оценка за контрольное задание по теме — зачтено, если зачтены все задачи данной темы. Оценка за контрольную работу — зачтено, если зачтены все контрольные задания по всем темам. Оформление контрольной работы следующее: на титульной странице название дисциплины, номер варианта, фамилия, имя, отчество студента, факультет, номер группы, рамка для
оценки контрольных заданий по всем темам вида:
| ∑ | |||||
Если практические задания по всем темам семестра выполнены на
оценку не ниже «удовлетворительно», и получена оценка «зачтено» за контрольную работу, то студент допускается к итоговой аттестации в семестре – зачету.
В случае неудовлетворительной оценки за практическое задание по отдельной теме студент должен выполнить работу над ошибками и прислать исправленное решение.
Если контрольная работа не зачтена, то студент также должен выполнить работу над ошибками и затем прислать исправленное решение.
Понятие системного подхода.
Системный подход представляет собой концептуальную основу современной методологии научного познания, имеющую принципиальное значение и в практической деятельности, особенно в областях, связанных с созданием и совершенствованием сложных технических и организационных систем и обеспечением их эффективного функционирования.
Именно на основе идей системного подхода возникли в последние десятилетия такие научные направления как общая теория систем, системотехника, исследование операций, системный анализ, кибернетика. Эти направления еще окончательно не сформировались, находятся в состоянии интенсивного развития, идет дискуссия об их границах и предметах исследования.
Однако огромные позитивные научные и прикладные достижения каждого из этих направлений общеизвестны. Системный подход, рожденный потребностями научно-технического и общественного прогресса, в свою очередь является его мощным катализатором.
Освещение философских и теоретических аспектов системного подхода не входит в задачу данного курса. Здесь мы лишь акцентируем свое внимание на некоторых положениях, вытекающих из концепции системного подхода, имеющих отношение к эффективности управления сложными организационными системами и, главным образом, – на связь системного подхода с математическим моделированием, как одним из основных средств реализации системного подхода в практике организационного управления.
В чем же новизна системного подхода как направления научного познания?
До возникновения системного мировоззрения основу научной методологии определял так называемый механистический метод анализа, суть которого заключается в том, что свойства целого можно объяснить исходя из свойств его частей. Механистическое мировоззрение – это развитие Лапласовской мысли о том, что Вселенную (или любую ее часть) можно познать, если известны законы, относящиеся к составляющим ее элементарным единицам. (Лаплас П.С. (1749-1827) – французский астроном, математик и физик. Ввел понятие механистического детерминизма как методологический принцип построения всякой науки).
Если не воспринимать чересчур прямолинейно, то основную идею механистического мировоззрения можно выразить так: «Целое есть сумма его частей, свойства целого есть сумма свойств частей, из которых оно состоит».
Таким образом, в основе исследования лежал анализ, т.е. изучение составляющих сложный объект элементов и их свойств и лишь затем, в редких случаях, предпринимались попытки исследовать их совместные действия, то есть осуществить попытки синтеза.
Методология такого подхода применительно к исследованию сложных систем не верна, во-первых, потому, что сложность нельзя познать на основе синтеза из простого, а, во-вторых, само выделение частей из целого (декомпозиция) и какие свойства частей и их взаимосвязи подлежат изучению – должно определяться исходя из системных соображений.
Механистический подход на определенном историческом этапе развития науки, безусловно, сыграл свою положительную роль. Наука накопила много знаний об отдельных фрагментах действительности,
открыла много частных законов (физических, химических, механических и т.п.). более того, с помощью математической статистики были решены проблемы, относящиеся к неорганизованной сложности (например, разработка теории газов).
Однако изучение объектов и явлений, для которых характерна организованная сложность, оказалось не под силу механистическому мировоззрению.
К началу второй половины ХХ века развитие общества, экономики, промышленности, осознание грядущих экологических проблем, весь ход научно-технического прогресса – поставили перед наукой и практикой задачи изучения и создания сложных систем, таких как природа в целом, организмы, социально-общественные образования, промышленные предприятия, системы вооружения, технические системы и
т.п.
Для этих систем характерна организованная сложность, способность к устойчивому целенаправленному поведению, несмотря на различные возмущающие воздействия. Целенаправленность, адаптация, саморегулирование, развитие и тому подобные атрибуты сложноорганизованных систем являются следствиями именно сложности этих систем. Оказалось, что сложные системы проявляют свойства, не присущие ни одному из составляющих их элементов (это явление получило название «эмерджентность» от англ. еmergent – внезапно возникающий). Многие свойства сложной системы содержатся не в ее элементах, а являются следствием взаимодействий этих элементов. Методы анализа, господствовавшие как основные методы научного познания, оказались бессильными или, по меньшей мере, – малопродуктивными при исследовании и создании сложных систем.
Тенденция исследовать и создавать системы как нечто целое, а не как конгломерат частей – вот основная идея системного мировоззрения.
Согласно этому мировоззрению главными являются закономерности, определяющие поведение целого. Отдельные элементы системы рассматриваются только в той степени, в какой их поведение имеет отношение к цели системы и к эффективности ее функционирования в
целом.
Особую значимость системное мировоззрение приобретает при решении проблем эффективного управления системами организационного типа, то есть теми системами, которые в качестве составляющих их элементов включают людей или их группы (отдельные исполнители, функциональные службы, коллективы цехов, участков, смен, бригад и
т.п.).
Эти составляющие организационных систем вырабатывают свои локальные цели и критерии, как правило, не совпадающие с глобальными целями и критериями эффективности системы в целом и зачастую противоречащие друг другу.
Именно осознание этого принципа (несовпадение глобальных и локальных целей и критериев) является одним из важнейших факторов в формировании системного образа мышления руководителя. Если нет четкого понимания того, что общесистемные цели являются главными, определяющими, то оптимизация деятельности локальных подразделений может привести к снижению эффективности организации в целом. Руководитель должен стремиться к суммарной эффективности своей организации и не допускать, чтобы частные интересы отдельных ее частей повредили общему успеху, и этого ему необходимо добиваться в условиях организационной среды, которая всегда содержит противоречащие друг другу цели. Он должен понимать, что достигнуть целей организации можно только в том случае, если рассматривать ее как единую систему, для чего необходимо оценить взаимодействия всех ее частей и объединить
их на такой основе, которая позволит организации в целом эффективно добиваться своих (глобальных) целей.
При этом оптимальное решение для системы (глобальный оптимум), как правило, ведет к тому, что отдельные части системы не достигают оптимального состояния в том смысле, как они это понимают, ибо то, что «хорошо» для системы в целом, чаще всего «не совсем хорошо» для отдельных ее элементов.
Это положение системного подхода кратко можно сформулировать как «несовпадение глобальных и локальных оптимумов».
Нахождение решений, направленных на достижение глобального оптимума, представляет собой основную проблематику эффективного управления системами организационного типа. Эта проблематика имеет два аспекта. Первый – создание или совершенствование самих организационных систем, как систем принятия решений (это направление часто называют системным проектированием). Второй аспект – это эффективное решение задач организационного управления, постоянно возникающих в процессе функционирования организационных систем, испытывающих воздействия как внешней среды, так и внутренние возмущающие воздействия.
Объективная необходимость повышения эффективности функционирования организационных систем потребовала создания научной методологии и специальных средств решения сложных организационных проблем.
Общетеоретическим фундаментом для решения этих проблем является кибернетика, как общая теория эффективного управления сложными динамическими системами независимо от их природы. Прикладные аспекты реализации системного подхода при решении организационных проблем разрабатывались в рамках таких научных направлений (комплексных дисциплин) как «исследование операций»,
«системный анализ», «теория принятия решений», «наука управления» и т.п. До настоящего времени нет единого мнения о том, являются ли эти названия дисциплин синонимами или за каждым из них кроется определенная специфика. Не будем и мы пока заниматься подобными исследованиями. Отметим лишь, что у этих направлений значительно больше общего, чем различий. Их методологическую основу составляют: системный подход, метод моделирования и принцип обратной связи.
Поскольку о системном подходе мы уже имеем некоторые представления, сейчас постараемся рассмотреть существо и роль моделирования для эффективного управления системами организационного типа. Именно моделирование является инструментом реализации системного подхода при принятии решений и организации процесса управления на принципе обратной связи. В процессе разработки управленческих решений моделирование играет роль, аналогичную лабораторным экспериментам в естественных науках и инженерной деятельности.
Принятие того или иного варианта решения предопределяет поведение объекта управления в течение определенного времени (периода планирования).
Тема 3. Дерево решений.
Выше мы рассматривали задачи, имеющие одно множество альтернативных решений и одно множество состояний среды. Многие задачи, однако, являются многоэтапными, когда одна совокупность стратегий игрока и состояний среды порождает другое состояние подобного типа, т.е. появляется целая цепочка решений, вытекающих одно из другого.
Дерево решений – это графическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды.
3.1. Некоторые задачи принятия решений и примеры использования деревьев решений.
Пример 5.Руководство некоторой компании решает, создавать ли для выпуска новой продукции крупное производство, малое предприятие или продать патент другой фирме. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния
рынка (табл. 11).
Таблица 11
| Номер стратегии | Действия компании | Выигрыш, при состоянии рынка | |
| благоприятном | неблагоприятном | ||
| крупное производство | 200 000 | – 180 000 | |
| малое предприятие | 100 000 | – 20 000 | |
| продать патент | 10 000 | 10 000 |
На основе данной таблицы строим дерево решений (рис 2.).
Крупное производство 1
благоприятное 200 000
состояние рынка
неблагоприятное
–180 000
|
3
М
100 000
Продать патент
Рис. 2. Дерево решений примера 5.
–20 000
10 000
Обозначения: – решение принимает игрок, – решение «принимает»
случай, – ожидаемая денежная оценка (ОДО) исхода.
Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ОДО.
Определим ожидаемую денежную оценку (ОДО) каждой вершины нашего дерева. Так как нам ничего не известно о вероятности благоприятного или неблагоприятного состояния рынка, то, согласно принципу неопределенности Лапласа, примем вероятность этих исходов равной 0.5, тогда
• для вершины 1 ОДО1=0.5×200000+0.5× (–180 000)=10000;
• для вершины 2 ОДО2=0.5×100000+0.5× (–20 000)=40000.
Таким образом, в вершине 3 целесообразно выбрать стратегию строить малое предприятие, ОДО этого (наилучшего) решения равна
40000.
Усложним пример 5.
Пусть перед принятием решения о строительстве руководство компании может обратиться к специализированной фирме, которая проведет исследование состояния рынка и уточнит вероятности исходов (за 10000 руб.). Возможности фирмы в части достоверности ее прогнозов
представлены в табл. 12.
Таблица 12
| Прогноз фирмы | фактически | |
| благоприятный | неблагоприятный | |
| благоприятный | 0.78 | 0.22 |
| неблагоприятный | 0.27 | 0.73 |
Например, когда фирма выдает прогноз, что рынок будет благоприятный, то этот прогноз оправдывается с вероятностью 0.78.
Предположим, что фирма выдала следующий прогноз:
• рынок будет благоприятный с вероятностью 0.45;
• рынок будет неблагоприятный с вероятностью 0.55.
На основании дополнительных сведений строим новое дерево решений
(рис 3.).
| Крупное производство | 1 благоприятное | 200 000 |
| состояние рынка |
3 Малое предприятие 2
(0,5)
неблагоприятное
(0,5) –180 000
благоприятное
Не проводить обследование
40000 (0,5) 100 000
40000 неблагоприятное –20 000 (0,5)
Продать патент 10 000
Крупное производство 4
благоприятное 200 000
116400 состояние рынка
(0,78)
неблагоприятное
(0,22) –180 000
Прогноз Малое предприятие благоприятное
благоприятный
73600
5 (0,78) 100 000
(0,45) 116400 неблагоприятное –20 000 (0,22)
Продать патент
Проводить 10 000
обследование 10
– 10000
|
а
Прогноз Малое предприятие благоприятное
–180 000
неблагоприятный 9
(0,55)
8 (0,27) 100 000
12400 неблагоприятное –20 000 (0,73)
Продать патент
10 000
Рис. 3. Дерево решений при дополнительном обследовании рынка
(в скобках показаны вероятности исходов)
Определим теперь ожидаемую денежную оценку (ОДО) каждой вершины нового дерева. Как и прежде
• для вершины 1 ОДО1=0.5×200000+0.5× (–180 000)=10000;
• для вершины 2 ОДО2=0.5×100000+0.5× (–20 000)=40000;
• для вершины 4 ОДО4=0.78×200000+0.22× (–180 000)=116400;
• для вершины 5 ОДО5=0.78×100000+0.22× (–20 000)=73600;
• для вершины 7 ОДО7=0.27×200000+0.73× (–180 000)= – 77400;
• для вершины 8 ОДО8=0.27×100000+0.73× (–20 000)=12400.
Значит, для вершины 3 выбираем ОДО3=40000,
для вершины 6 выбираем ОДО6=116400,
для вершины 9 выбираем ОДО9=12400,
тогда ОДО10=0.45×116400+0.55×12400=59200,
и ОДО11=59200 – 10000=49200.
Анализируя дерево решений, можно сделать следующие выводы:
• целесообразно проводить дополнительное обследование состояния рынка, ОДО этого решения равна 49200 (с учетом стоимости затрат на обследование), тогда как без обследования только 40000;
• если прогнозируется благоприятная ситуация на рынке, то необходимо строить большое предприятие (ОДО=116400), если прогноз
неблагоприятный – малое предприятие (ОДО=12400).
В условиях данного примера рассчитаем ожидаемую ценность достоверной информации (см. 2.4). При отсутствии точной информации ОДО=40000. Если точная информация о состоянии рынка будет благоприятной, то необходимо строить большое предприятие (ОДО=200000), если неблагоприятной, то целесообразно продать патент (ОДО=10000). Предполагая, до обращения к экспертам, что вероятности благоприятной и неблагоприятной ситуаций равны 0.5, вычисляем ОДО точной информации
ОДОт.и = 0.5×200000+0.5×10 000)=105000.
Тогда ожидаемая ценность достоверной информации равна
105000 – 40000=65000.
Это значение показывает, какую максимальную цену может заплатить компания за точную информацию об истинном состоянии рынка.
Парадокс Алле.
Рассмотрим две лотереи (рис. 4).
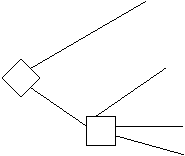
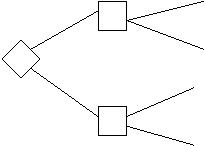1 млн С 0.1 5 млн
А 0.9
0.1 5 млн
В D 0.11 1 млн
0.89
1 млн
0.01 0 0.89 0
Рис. 4. Дерево решений двух лотерей
Примем значение функции полезности U(5 млн)=100, U(0)=0 и пусть
U(1 млн)= U.
В левой лотерее подавляющее большинство людей (не склонных к авантюризму) предпочитает альтернативу А (получить 1 млн. без риска) альтернативе В (принять участие в лотерее, где есть вероятность ничего не выиграть), т.е. полезность альтернативы А оценивается выше, чем полезность альтернативы В. Следовательно,
U > 0.1×100+0.89×U, откуда U > 10/0.11.
В правой лотерее подавляющее большинство людей предпочитает альтернативу С (почти та же вероятность выиграть, что и в D, но выигрыш существенно больше). Значит
0.1×100 > 0.11×U, откуда U < 10/0.11.
Мы видим, что в данном случае люди поступают не в соответствии с функцией полезности.
Рассмотрим еще один пример двух лотерей (рис. 5).
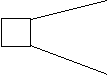
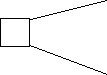0.6 50 0.5 44
0.4 – 20 0.5 0
Рис. 5. Сравнение двух лотерей
Ожидаемая денежная оценка обеих лотерей одинаковая
(0.6×50 – 0.4×20=0.5×44=22),
однако предъявление различным группам людей этих пар лотерей показало, что люди предпочитают правую лотерею, где риск проигрыша исключен.
Вышеприведенные примеры показывают огромную роль лица,
принимающего решение (ЛПР), его опытность, отношение к риску и т.п.
Нерациональное поведение.
Принятие решения ЛПР не в соответствии с максимизацией ожидаемой полезности будем называть нерациональным поведением.
Причины отклонения поведения людей от рационального связаны не только с их личностными качествами, но и с формулировкой альтернатив. Рассмотрим пример «дилемма генерала».
Есть две возможные дороги для вывода войск (600 чел.) из окружения,
данные о возможных исходах потерь людей представлены на рис. 6.
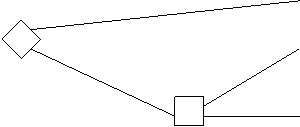Дорога 1 400 чел. погибнут
Дорога 2
1/3
Никто не погибнет
2/3 Все 600 чел. погибнут
Рис. 6. Дилемма генерала (исходы в виде потерь)
Большинство людей, рассматривающих данную дилемму, выбирают первую дорогу, стараясь избежать исхода, когда погибает весь отряд.
Но эта же дилемма была представлена испытуемым в виде исходов спасения людей (рис. 7).
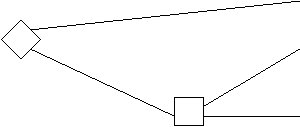Дорога 1 200 чел. спасены
Дорога 2
1/3
Все 600 чел. спасены
2/3 0 чел. спасены
Рис. 7. Дилемма генерала (исходы в виде спасения людей)
Теперь уже большинство испытуемых людей выбирают вторую дорогу,
так как на ней с вероятностью 1/3 можно спасти весь о