Ответ: максимума функция достигает в точке (1; 7/12) и в точке (1; -2 1/12). В точке (2/3; 50/81) – минимум функции.

25 Понятие первообразной функции. Понятие неопределенного интеграла.

Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Неопределённый интегра́л для функции 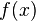— это совокупность всех первообразных данной функции

Функция F (х) называется первообразной функцией для данной функции f (х) (или, короче, первообразной данной функции f (х)) на данном промежутке, если на этом промежутке

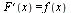
. Пример. Функция 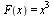является первообразной функции 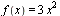на всей числовой оси, так как 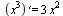при любом х.
Отметим, что вместе с функцией 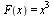первообразной для 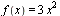является любая функция вида 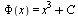, где С — произвольное постоянное число (это следует из того, что производная постоянной равна нулю). Это свойство имеет место и в общем случае.

Теорема 1. Есл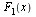и и 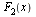— две первообразные для функции f (х) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу.
Из этой теоремы следует, что если известна какая-нибудь первообразная F (х) данной функции f (х), то все множество первообразных для f (х) исчерпывается функциями F (х) + С.
Выражение F (х) + С, где F (х) — первообразная функции f (х) и С — произвольная постоянная, называется неопределенным интегралом от функции f (х) и обозначается символом ,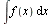
причем f (х) называется подынтегральной функцией ;
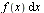— подынтегральным выражением,
х — переменной интегрирования;
∫ —знак неопределенного интеграла.
Таким образом, по определению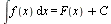
если .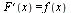
Возникает вопрос: для всякой ли функции f (х) существует первообразная, а значит, и неопределенный интеграл?
Теорема 2. Если функция f (х) непрерывна на [a ; b], то на этом отрезке для функции f (х) существует первообразная.
Ниже мы будем говорить о первообразных лишь для непрерывных функций. Поэтому рассматриваемые нами далее в этом параграфе интегралы существуют.

26 Основные свойства неопределенного интеграла, основные табличные интегралы (формулы).

1) Производная неопределенного интеграла равна подынтегральной функции. Дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е. (∫f(x)dx)′=f(x)d∫f(x)dx=f(x)dx

Доказательство:

∫f(x)dx=F(x)+C,

(∫f(x)dx)′=(F(x)+C)′=F′(x)+0=F′(x)=f(x),

d∫f(x)dx=(∫f(x)dx)′dx=f(x)dx

2) Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е. ∫dF(x)dx=F(x)+C .

Доказательство:

dF(x)=F′(x)dx=f(x)dx,

∫dF(x)dx=∫f(x)dx=F(x)+C.

3) Постоянный множитель можно выносить из под знака интеграла, т.е. ∫kf(x)dx=k∫f(x)dx,k/=0

Доказательство: Пусть F(x) -- первообразная для функции f(x), тогда
kF(x) -- первообразная для функции kf(x).

(kF(x))′=0+kF′(x)=kF′(x)=kf(x).

Таким образом

∫kf(x)dx=kF(x)+C=k(F(x)+C/k)=k(F(x)+C1)=k∫f(x)dx

4) Неопределенный интеграл от суммы(разности) двух функций равен сумме(разности) интегралов этих функций.

∫[f(x)±g(x)]dx=∫f(x)dx±∫g(x)dx

Распространяется на n слагаемых.

Доказательство:

d[∫f(x)dx±∫g(x)dx]=d∫f(x)dx±d∫g(x)dx=

=f(x)dx±g(x)dx=[f(x)±g(x)]dx.

Возвращаясь к той механической задаче, которая была поставлена вначале, можно теперь написать, что v=∫a(t)dt и s=∫v(t)dt .

Предположим для определенности: движение равноускоренное, например, происходит под действием силы тяжести; тогда a=g (если направление вертикали вниз считать положительным) и v=∫gdt=gt+C .

Получили выражение для скорости v, в которое, кроме времени t, входит еще и произвольная постоянная С. При различных значениях С получаются и различные значения для скорости в один и тот же момент времени; следовательно, имеющихся данных недостаточно для полного решения задачи. Чтобы получить вполне определенное решение задачи, достаточно знать величину скорости в один какой-нибудь момент времени. Например, пусть известно, что в момент t=t0 скоростьv=v0, подставим эти значения в полученное выражение для скорости v0=gt0+C, откуда C=v0−gt0 , и теперь решение принимает определенный вид: v=g(t−t0)+v0 .

Найдем, далее, выражение для пути s. Имеем

s=∫[g(t−t0)+v0]dt=g(t−t0)2/2+v0(t−t0)+C′

Неизвестную новую постоянную C′ можно установить, если, например, дано, что путь s=s0 в момент t=t0; найдя, что C′=s0 , получаем решение в окончательном виде s=g(t−t0)2/2+v0(t−t0)+s0 .

Значения t0, s0,v0 условно называется начальными значениями величин t,s,v.

Точно так же можно написать: m=∫ρ(x)dx .

И здесь при интегрировании появится постоянная C, которая определяется из того условия, что при x=0 и масса m должна обратиться в нуль.