Анализ оптимального решения ТЗ. Рекуррентная формула расчета целевой функции.

На первом шаге значение целевой функции определяется как сума произведений тарифов на соответствующие объёмы грузов (сума от j=1 до n Сума от i=1 до m Cij*Xij). На всех последующих шагах также можно пользоваться этой формулой. Однако гораздо меньше вычислений даёт рекуррентная формула. F(Xi)=F(X(i-1)) –(если min) + (если max) Гама*Дельтаij где Гама – величина перераспределяемого груза, Дельтаij – оценка свободной клетки с которой начинается построение цикла.

Анализ оптимального плана. 1. Необходимо указать от какого поставщика к какому потребителю и в каком количестве направляется груз. Если был введён фиктивный поставщик (т.е. <запасов) то необходимо указать кто и в каком количестве недополучил груз. Если вводится фиктивный потребитель, то указывают поставщика и количество у которого остался не вывезенный груз. 2. Необходимо сделать выводы о количестве оптимальных решений. Если среди оценок свободных клеток последнего оптимального плана есть хоть одна нулевая (Дельтаij=0) то оптимальный план не единственный. Будет существовать альтернативный оптимум. Его можно найти построив цикл для клетки с нулевой оценкой и перераспределить груз. Зн

45. Графическое решение матричной игры размерностью 2 × 2.

Графическим методом можно решить игру, если хотя бы одна из размерностей платёжной матрицы равна двум.

Рассмотрим платёжную матрицу 2*2,

	В1	В2
А1	А11	А12	P1
А2	А21	А22	P2
	Q1	Q2

НА координатной плоскости по оси абсцисс отмечаем единич. Отрезок и проводимчерез точку (1;0) прямую перпендикулярно данной оси.

На полученной прямой отмечаем выигрыш 1-го игрока при использовании им с.тратегии А1.

На оси ординат отмечаем выигрыш 1-го игрока, при использовании стратегии А2.

Соединим значения соответствующие проигрышам 2-го игрока при использовании им страт-ииВ1 (а11, а21), и стратегии В2 (а12, а22).

В результате получим прямые В1В1 и В2В2; N=В1В1 ÇВ2В2 . N=(р1;g).

Первая координата этой точки соответствует вероятности применения первым игроком стратегии А1, а вторая координата этой точки соответствует цене игры g.

А1 А2

В2 а 12

а 21 В1 N

а 22 В2

g а 11 В1

О р1 р2 1

А2 А1

40. Основные понятия теории игр.

Теория игр (ТИ) занимается разработкой различного рода рекомендаций по принятию решений в условиях конфликтных ситуаций.

Формализация конфликтных ситуаций с помощью математического языка позволяет представить конфликт как игру двух-трех или более сторон. Каждая сторона преследует цель максимизировать свой выигрыш за счет других игроков.

Достаточно часто теорию игр определяют как раздел математики, занимающийся выработкой оптимальных правил поведения для каждой стороны конфликтной ситуации.

Стороны, участвующие в конфликтной ситуации, называются игроками.

Совокупность правил, однозначно определяющих последовательность действий сторон в конкретной игре, называются стратегиями.

Игра – совокупность предварительно оговоренных правил и условий или формализованная модель конфликта.

Пот термином «партия» поминают частичную возможность реализации оговоренных правил или одной реализацию игры.

Для задания игры необходимо определить:

1) Варианты действий игроков

2) Объем информации каждого игрока о поведении противника

3) Выигрыш или исход конфликта, к которому приходит совокупность действий игроков

Развитие игры во времени происходит по ходам – выбор и реализация какой-либо стратегии игрока. Ходы бывают личными и случайными.

Личный ход – сознательный выбор игроком одного из вариантов поведения. ДАЛЬШЕ МАРИНА ПИШЕТ.

41. Классификация игр.

1) Классификация в зависимости от причин, вызывающих неопределенность исхода: комбинаторные, азартные, стратегические.

В комбинаторныхиграх существует возможность рассматривать все исходы, но этих исходов настолько много, что обычно игра не в состоянии это сделать

Неопределенность исхода азартных игр связана с влиянием случайных факторов. Азартные игры состоят только из случайных ходов. Теория игр азартными играми не занимается.

В стратегических играх неопределенность исходов связана с тем, что игрок не знает о тех стратегиях, которых придерживаются другие игроки.

2) Классификация по количеству игроков: парные (2 игрока), множественные (больше 2х игроков).

Во множественных играх игроки могут объединяться в коалиции постоянные или временные. Если существуют 2 постоянные коалиции, то она становится парной.

3) По количеству возможных ходов: одношаговые, многошаговые.

4) По количеству возможных стратегий: конечные, бесконечные (хотя бы у 1 игрока бесконечное число стратегий).

5) По сумме выигрыша: с нулевой суммой, с ненулевой суммой.

В играх с нулевой суммой одни игроки выигрывают за счет других, а суммарный выигрыш и суммарный проигрыш равны.

В играх с ненулевой суммой часть выигрыша может достаться «третьей стороне».

Парная игра с нулевой суммой называется антагонистической.

42. Понятие матричной игры. Принцип минимакса. Понятие Седловой точки.

Рассмотрим игру 2х игроков. Игрок А имеет m возможных стратегий {A1, A2, …, Am}. У игрокаB n возможных стратегий {B1, B2, …, Bn}.

Если игрок А выберет свою стратегию Аi, а игрок В ответит при этом стратегией Bj, то эти стратегии однозначно определят исход игры для каждого игрока: аij – исход игры для 1 игрока, bij – для второго. Для удобства все эти исходы записывают в виде платежных матриц.

(тут обычная матрица Аmxn и Bmxn)

Игру, заданную двумя платежными матрицами, называют биматричной.

Если рассмотреть антагонистическую игру, то в ней интересы игроков противоположны: сколько выигрывают один, столько же проигрывает другой. Матрицы таких игроков будут состоять из противоположных по знаку, но одинаковых по модулю элементов aij=-bij. В этом случае нет необходимости использовать обе матрицы. Ограничимся только матрицей А, в которой любое положительное число трактуется как выигрыш игрока А, а любое отрицательное число – выигрыш игрока В. Игру в этом случае называют матричной.

Замечание: Любую платежную матрицу можно привести к положительному виду, а значит трактовать ее как матрицу выигрышей первого игрока. Для этого среди всех отрицательных чисел выбирают наибольшее по модулю и прибавляют данный модуль к каждому элементу матрицы.

Решение игры в чистых стратегиях.

Пусть задана антагонистическая матричная игра

Рассмотрим каждую стратегию первого игрока и определим минимальную возможный выигрыш по ней.

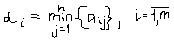- какую бы стратегию не выбрал первый игрок, второй ответит так, чтобы его проигрыш, а значит выигрыш первого, был минимален. Тогда для первого игрока оптимальной будет та стратегия, при которой он получит максимум выигрыша из всех минимумов.

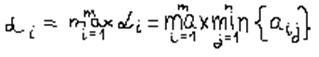- альфа называют нижней ценой игрыили максимином.

Таким образом, оптимальной будет считаться та стратегия первого игрока, при которой достигается нижняя цена игры (A_i^* - оптимальная стратегия первого игрока).

Если второй игрок выберет любую свою стратегию Вj, то первый игрок ответит такой стратегией, чтобы проигрыш второго игрока был максимальным. Второму игроку в этом случае выгодно принять такую стратегию, при которой из всех максимальных проигрышей получится минимальный.

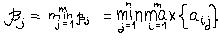- бэтта называют верхней ценой игры или минимаксом.

Оптимальной стратегией второго игрока В_j^*будет та стратегия, при которой достигается верхняя цена игры β.

α≤β всегда (верхняя цена игры не меньше, чем нижняя).

Если верхняя и нижняя цена игры совпадают, то есть α=β, то говорят, что игра имеет седловую точку. В этом случае интересы 2х игроков совпадают и игра имеет решение в чистых стратегиях.

Оптимальные стратегии характеризуются устойчивостью.

При разумном подходе каждого игрока 1й игрок точно может рассчитывать на выигрыш α, а 2й игрок точно проиграет сумму β. В случае ошибки противника выигрыш может быть больше α, а проигрыш – меньше β.

43. Решение матричной игры в смешанных стратегиях.

Если α<β, то есть игра не имеет седловую точку, то интересы игроков не совпадают и определить оптимальные чистые стратегии нельзя. Тогда необходимо для каждого игрока определить вектор частот, с которым следует применять каждую стратегию каждого игрока. Если рассмотреть не сами частоты, в относительные частот, то можно говорить о вероятностях применения стратегий каждого игрока.

Обозначим эти вероятности через р_i (i = 1,m) – для первого игрока, q_j (j = 1,n) для второго игрока.

Таким образом, для игрока А вектор смешанных стратегий примет вид:

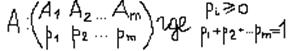
Для игрока В вероятность смешанных стратегий определяется аналогично.

Средний выигрыш первого игрока можно определить как математическое ожидание векторов p и q.

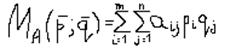
Стратегии р* и q*, при которых достигается средний выигрыш М_а называются оптимальными смешанными стратегиями в том случае, если выполняется условие:

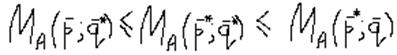
Средний выигрыш, при котором достигаются оптимальные стратегии, называется ценой игры:

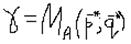
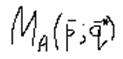- означает, что отклонение игрока А от своей оптимальной стратегии, при условии, что игрок В придерживается своей оптимальной стратегии, приводит к уменьшению среднего выигрыша игрока А.

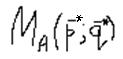- означает, что отклонение игрока В от своей оптимальной стратегии, при условии, что игрок А придерживается своей оптимальной стратегии, приводит к увеличению среднего проигрыша игрока В, а значит к увеличению выигрыша игрока А.

ТЕОРЕМА ФОН-НЕЙМОНА

Каждая конечная матичная игра имеет по крайней мере 1 оптимальное решение, возможно. Среди смешанных стратегий.

Для определения смешанных стратегий существует несколько методов, однако перед их применением можно постараться упростить платежную матрицу.

Упрощение платежной матрицы:

1) Исключаем дублирующие стратегии, т.е. вычеркиваем повторяющиеся строки/столбцы. При этом вероятности отброшенных стратегий считаем = 0.

2) Выясняем наличие доминирующих стратегий. Если какая-либо стратегия доминирует над другой, то оставляем ее, а заведомо проигрышную вычеркиваем.

- Для игрока А доминирующей считается та стратегия, для которой все возможные выигрыши не меньше, чем соответствующие выигрыши другой стратегии;

- Для игрока В доминирующей считается та стратегия, для которой все возможные проигрыши не превосходят соответствующих проигрышей другой стратегии.

3) После вычеркивания к оставшейся матрице вновь применяем указанные правила и повторяем до тех пор, пока вычеркнуть уже ничего нельзя.

При упрощении платежной матрицы необходимо следить за тем, какие стратегии исключаем. Нумерацию стратеги менять НЕЛЬЗЯ!

44. Алгебраический метод решения матричной игры размером 2х2.

Если в результате упрощения получилась матрица размерностью 2х2, то игру можно решать аналитически или графически.

Рассмотрим аналитическое решение:

Необходимо определить смешанные стратегии первого игрока и второго игрока 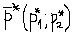и .

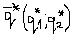Для 1го игрока цена игры α и оптимальные смешанные стратегии можно найти из системы:

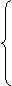а₁₁р₁+а₂₁р₂=α

а₁₂р₁+а₂₂р₂=α

р₁+р₂=1

Аналогично можно провести рассуждения для 2го игрока:

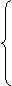а₁₁q₁+а₂₁q₂=α

а₁₂q₁+а₂₂q₂=α

q₁+q₂=1

Решив эти системы найдем оптимальные стратегии для каждого игрока.

46. Графическое решение матричных игр размерностью 2 × n и m × 2.

Это игра у которой 1-ый игрок обладает 2-мя стратегиями, а у второго игрока n возможных стратегий.

	В1	В2	…..	Вn
А1	а 11	а 12	……	а 1n
А2	а 21	а 22	…….	а 2n

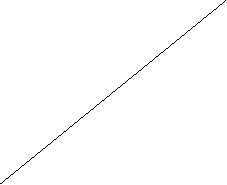
Для решения данной игры необходимо найти для 1-го ирока вероятности р1 и р2; для этого на координатной плоскости отмечаем т. (1;0) и проводим через неё перпендикуляр к оси абсцисс. Назовем этот перпендик-р А1А1 и отметим на нем все выигрышные стратегии А1.

Ось ординат обозначим А2А2 и отметим на ней все выигрышные стратегии А2 (а21, а22, .., а2n),. Соединим значения соответствующие проигрышам 2-го игрока при использовании стратегий В1 (а11, а21), В2 (а12, а22),…., Вn (a1n, a2n).

Выделим среди пересечений прямых В1В1, В2В2,…., ВnBn нижнюю огибающую.

На данной огибающей найдём т. MAX, и обозначим её N (р1; g).

А2 А1

а 2n Bn

B2 a 12

a 21 B1

N B1 a 11

a 22 B2 g

Bn a 1n

О 1

А2 р1 р2 А1

Для матрицы m*2.

В данной игре 1-ый игрок имеет m-стратегий, а второй только 2.

	В1	B2
А1	а 11	a 12
А2	а 21	a 22
……	……	……
Аm	а m1	a m2

в результате применения графического метода можно найти вероятности применения стратегий вторым игроком, т. е. q1 и q2.

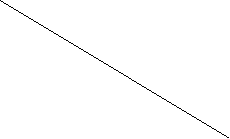
Построение выполняется аналогично игре 2*n, но перпендикуляр , проходящий через т. (1;0) обозначается В1В1 и на нем откладывается проигрыш 2-го игрока при использовании стратегии В1 (а 11, а 21, …, аm1).

Ось ординат обозначается В2В2 и на ней откладываются соответствующие проигрыши стратегии В2 (а12, а22, аm2).

Соединяем значении соответствующей стратегии А1 (а11, а12), А2 (а21, а22), …., Аm (am1,am2).

Выделим верхнюю огибающую от пересечения прямых А1А1, А2А2, …, АmAm. Точка MIN этой огибающей обозначим через N (q1;g).

В2 В1

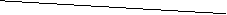
а m2 Am A2 a 21

a 12 A1 N A1 a 11

Am am1

a 22 A2 g

O 1 q

В2 q1 q2 В1