Евклидово пространство: точки, множества, сходимость
Евклидово пространство: точки, множества, сходимость
IТочки, множества
Определение 1. Назовем m-мерной точкой упорядоченный набор из m произвольных вещественных чисел х1, х2, … хm. Обозначения : М(х1, х2, … хm) или 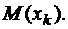 Множество всех мыслимых m-мерных точек называют m-мерным эвклидовым пространством, если расстояние между точками М(хk) и N(уk) определяется по формуле
Множество всех мыслимых m-мерных точек называют m-мерным эвклидовым пространством, если расстояние между точками М(хk) и N(уk) определяется по формуле
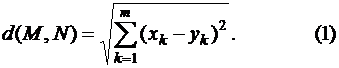

Обозначения : Rm или Em. Числа хk, k = 1,2…m, называют координатами точки М(хk), а точку О(0,0,…0) – началом координат.
Частными случаями евклидова пространства являются R2(плоскость) и R3 (обычное пространство). Формула (1) является естественным обобщением известных формул для расстояния между двумя точками на плоскости и в пространстве.
Для классификации точек и множеств в Rmважную роль играет понятие окрестности.
Определение 2. ε-окрестностью точки М0 называют множество точек вида
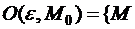
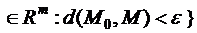 . В R1 – это интервал (x0– ε, x0+ ε), в R2 – внутренность круга, с центром в М0 и радиусом ε, а в R3 – внутренность сферы с центром в М0, и радиусом ε.
. В R1 – это интервал (x0– ε, x0+ ε), в R2 – внутренность круга, с центром в М0 и радиусом ε, а в R3 – внутренность сферы с центром в М0, и радиусом ε.
Определение 3. Точка М0 называется внутренней точкой множества G 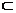 Rm, если существует ε такое, что О(ε,М0)
Rm, если существует ε такое, что О(ε,М0) 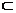 G. Точка М0 называется граничной точкой множества G, если всякая ее ε-окрестность содержит как точки, принадлежащие G, так и точки не принадлежащие G.
G. Точка М0 называется граничной точкой множества G, если всякая ее ε-окрестность содержит как точки, принадлежащие G, так и точки не принадлежащие G.
Определение 4. Множество точек называется открытым, если все его точки внутренние. Множество точек называют замкнутым, если оно содержит все свои граничные точки.
Примером открытого множества может служить ε-окрестность. Замкнутым множеством в R2 есть, например, прямоугольник {(х,у) : 0 ≤ х ≤ a, 0 ≤ y ≤ b}. Все пространство Rm и пустое множество ø являются и открытыми и замкнутыми одновременно.
Определение 5. Множество точек называется связным, если любые две его точки можно соединить непрерывной линией, которая состоит из точек данного
множества.
Например, в R2 круг – это связное множество, а множество, состоящее из двух непересекающихся кругов, не является связным.
Определение 6. Открытое связное множество называется открытой областью или, короче говоря, областью. Объединение открытой области со всеми ее граничными точками называется замкнутой областью.
Можно доказать, что замкнутая область есть замкнутое множество.
Определение 7. Множество точек G 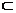 Rm называется ограниченным, если целиком содержится в некотором m-мерном “шаре”:
Rm называется ограниченным, если целиком содержится в некотором m-мерном “шаре”:
G 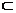 {M: d(О, M) ≤ R}.
{M: d(О, M) ≤ R}.
Ограниченными являются m-мерный “параллелипипед” (замкнутый):
{M(xk): ak ≤ xk ≤bk , k = 1,2,…m}
и m-мерный “симплекс”(открытый):
{M(xk): x1 + x2 +…+ xm< a, xk > 0,k = 1,2…m}.
Отметим для будущего, что ограниченная замкнутая область для функции нескольких переменных является аналогом замкнутого промежутка для функции одной переменной.
.
II Сходимость
Рассмотрим в Rm последовательность точек
{Mn(x1n, x2n,…, xmn)}, n = 1,2 … .
Определение 8. Говорят, что последовательность{Mn} сходится к точке М0(а1, а2,… аm) и пишут 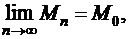 если
если 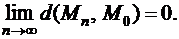
Из формулы (1),определяющейрасстояние между точками в Rm, нетрудно получить такое утверждение:
cходимость {Mn} к M0равносильна сходимости последовательностей {xkn} к аk, k = 1,2,…m. Другими словами, сходимость точек в Rm покоординатная.
Например, последовательность двумерных точек Мn 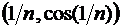 сходится к точке М0(0,1).
сходится к точке М0(0,1).
Примеры.
1. Так как sinα ~ α, при α → 0, то
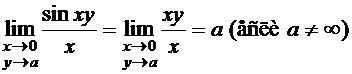 .
.
2. Рассмотрим функцию 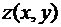
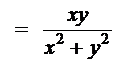 и последовательность точек
и последовательность точек
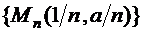 , сходящаяся к началу координат O(0,0). Соответствующая последовательность значений функции
, сходящаяся к началу координат O(0,0). Соответствующая последовательность значений функции
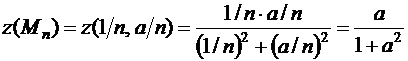
имеет предел, зависящий от последовательности {Mn}. Следовательно, предел функции в начале координат не существует.
Определение 2. Функция z(x,y) называется непрерывной в точке 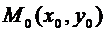 , если
, если
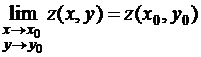 . (1)
. (1)
Определение 3. Функция z (x,y) называется непрерывной в области G, если она непрерывна в каждой точке 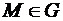 .
.
Свойства ФНП, непрерывной в ограниченной замкнутой области, аналогичны свойствам функции одной переменной, непрерывной на замкнутом промежутке. Приведем некоторые из них.
1) Функция z(х,y), непрерывная в ограниченной замкнутой области 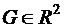 , ограничена в
, ограничена в 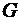 , и достигает наибольшего и наименьшего значений.
, и достигает наибольшего и наименьшего значений.
2) Если z(х,y) 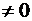 , то в некоторой окрестности точки
, то в некоторой окрестности точки 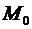 функция сохраняет знак.
функция сохраняет знак.
Замечание. Соотношению (1), определяющему непрерывность функции в точке, можно придать другую форму.
Будем называть полным приращением функции z(x,y) в точке 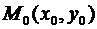
разность:
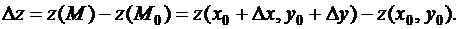
Если обозначить 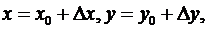 то нетрудно получить утверждение:
то нетрудно получить утверждение:
непрерывность функции z(x,y) в точке 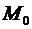 равносильна равенству
равносильна равенству
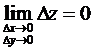 .
.
Лекция 18
Частные производные
Пусть функция z(x,y) определена в некоторой окрестности точки 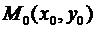 . Придадим переменной x приращение
. Придадим переменной x приращение 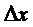 , т.е. перейдем от точки
, т.е. перейдем от точки 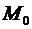 к точке
к точке 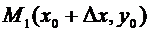 . При этом
. При этом 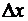 таково, что
таково, что 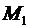 лежит в указанной окрестности точки
лежит в указанной окрестности точки 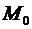 . Тогда соответствующее приращения функции
. Тогда соответствующее приращения функции
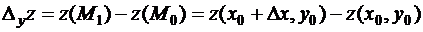
называется частным приращением функции z(x,y) в точке 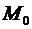 .
.
Аналогично определяется частное приращение функции по переменной 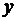 :
:
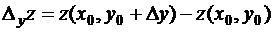 .
.
Определение. Предел вида 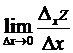 называется частной производной функции z(x,y) в точке
называется частной производной функции z(x,y) в точке 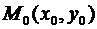 по переменной
по переменной 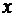 и обозначается одним из символов:
и обозначается одним из символов:
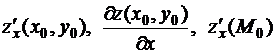 .
.
Аналогично определяется и частная производная по переменной 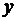 :
:
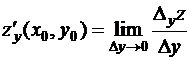 .
.
Из определения следует, что частная производная функции двух переменных по переменной 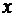 представляет собой обычную производную функции одной переменной f(x) = z(x,y0). Поэтому частные производные вычисляются по формулам и правилам вычисления производных функций одной переменной.
представляет собой обычную производную функции одной переменной f(x) = z(x,y0). Поэтому частные производные вычисляются по формулам и правилам вычисления производных функций одной переменной.
Примеры.
1. 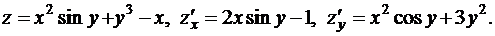
2. 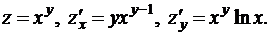
Замечание. График функции z = z(x,y) есть некоторая поверхность в пространстве. Тогда
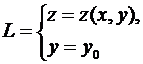 –
–
это некоторая кривая (плоская) в пространстве и 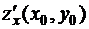 есть не что иное, как угловой коэффициент касательной к L в точке (
есть не что иное, как угловой коэффициент касательной к L в точке ( 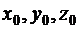 ).
).
Производные сложных функций
Приведем без доказательства ряд формул дифференцирования сложных функций. Все встречающиеся функции одной или нескольких переменных считаем дифференцируемыми.
1. Если 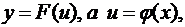 то
то
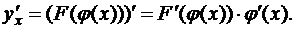
2. Если 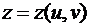 , а
, а 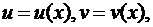 то для сложной функции одной переменной z(u(x),v(x))имеем
то для сложной функции одной переменной z(u(x),v(x))имеем
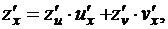
или используя другие обозначения,
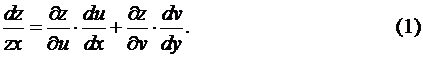
В частности, если 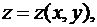 а
а 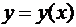 , то
, то

В этом случае производную 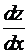 называют полной производной, в отличие от
называют полной производной, в отличие от 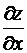 – частной производной.
– частной производной.
3. Если 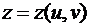 , а
, а 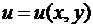 и
и 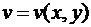 , то для сложной функции двух переменных
, то для сложной функции двух переменных 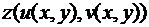 имеем:
имеем:
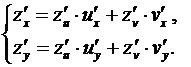 (3)
(3)
Замечание 1. Формулы (1), (2), (3) легко обобщаются на случай функций трех и более переменных.
Замечание 2.Формулы (1), (2), (3) необходимы в теории для получения других важных результатов. На практике в случае конкретных функций нетрудно исключить зависимость функции от промежуточных переменных. Например, если
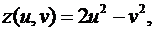 а
а 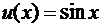 и
и 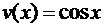 , то
, то 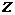 как функция
как функция 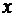 имеет вид
имеет вид 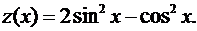
III Уравнения касательной
Линию в пространстве обычно задают системой параметрических урав-нений
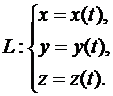
Однако, удобно такую линию понимать как годограф вектор-функции
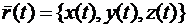 .
.
Напомним, что, кратко говоря, касательная к линии L в ее точке 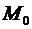 –это пре-дельной положение секущей
–это пре-дельной положение секущей 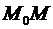 , когда точка
, когда точка 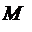 стремиться к
стремиться к 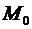 вдоль L. Другими словами, касательная в точке
вдоль L. Другими словами, касательная в точке 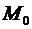 – это та прямая, проходящая через
– это та прямая, проходящая через 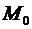 , направляющий вектор которой есть предел направляющего вектора секущей. Пусть
, направляющий вектор которой есть предел направляющего вектора секущей. Пусть 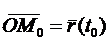 и
и 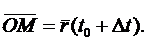 Тогда
Тогда
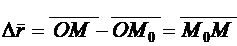 ,
,
т.е. 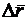 , а следовательно и
, а следовательно и 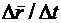 служат направляющими векторами секущей. Поэтому
служат направляющими векторами секущей. Поэтому
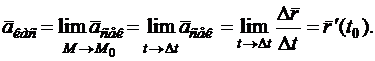
Отсюда получаем два вывода:
1)вектор мгновенной скорости точки направлен по касательной к траек-тории движения;
2)канонические уравнения касательной к линии L в точке 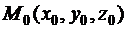 , которая соответствует значению параметра
, которая соответствует значению параметра 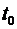 , имеют вид:
, имеют вид:
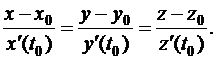
Пример. Показать, что касательные к линии 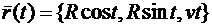 образуют с осью
образуют с осью 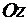 постоянный угол.
постоянный угол.
Решение. Для винтовой линии направляющий вектор касательной 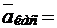
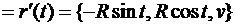 . Если
. Если 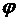 – угол между касательной и осью
– угол между касательной и осью 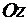 , то
, то
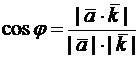 .
.
Напомним, что 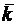 – орт оси
– орт оси 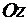 :
: 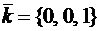 . Значит,
. Значит,
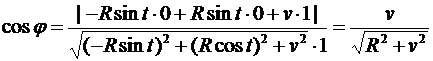 .
.
Как видим, 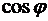 , а значит и
, а значит и 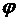 , не зависят от параметра t, т.е
, не зависят от параметра t, т.е 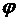 = сonst.
= сonst.
Замечание. Нетрудно заметить, что для плоской линии
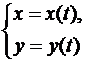
уравнение касательной имеет вид
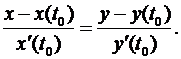
Пример. Составить уравнение касательной к эллипсу 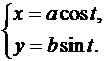
Решение. Пусть 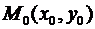 – точка касания, соответствующая значению параметра
– точка касания, соответствующая значению параметра 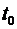 :
: 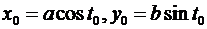 . Тогда уравнение касательной:
. Тогда уравнение касательной:
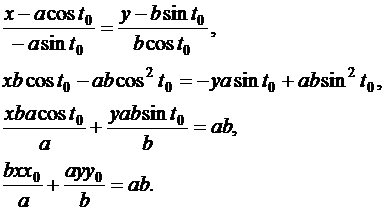
Разделив обе части последнего равенства на а .b, получим известную формулу для касательной к эллипсу в его точке 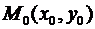 :
:
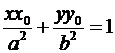 .
.
Производные высших порядков
Если функция 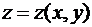 имеет частные производные
имеет частные производные 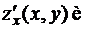
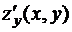 в каждой точке некоторой области
в каждой точке некоторой области 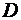 , то они представляют собой функции двух переменных, определенные в
, то они представляют собой функции двух переменных, определенные в 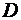 . Может случиться, что эти функции имеют в
. Может случиться, что эти функции имеют в 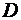
частные производные. Тогда эти производные называются частными производ-ными второго порядка
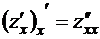 ,
, 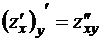 ,
, 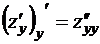 ,
, 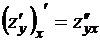 .
.
Используются и другие обозначения, например:
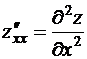 ,
, 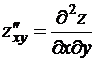 .
.
Производные 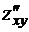 и
и 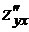 называются смешанными производными второго поряд-ка. При некоторых условиях смешанные производные не зависят от порядка диф-ференцирования.
называются смешанными производными второго поряд-ка. При некоторых условиях смешанные производные не зависят от порядка диф-ференцирования.
Теорема. Пусть функция 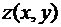 имеет в области
имеет в области 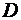 частные производные
частные производные 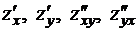 . Пусть, кроме того, смешанные производные
. Пусть, кроме того, смешанные производные 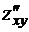 и
и 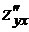 непре-рывны в
непре-рывны в 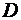 . Тогда имеет место равенство
. Тогда имеет место равенство
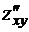 =
= 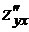 .
.
Аналогично производным второго порядка вводятся частные производные третьего, четвертого, …, 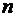 -го порядка. Для смешанных производных высших по-рядков остается справедливой сформулированная выше теорема.
-го порядка. Для смешанных производных высших по-рядков остается справедливой сформулированная выше теорема.
II Градиент
Определение 2. Вектор, проекциями которого служат частные производные функции 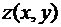 , называется градиентом функции
, называется градиентом функции
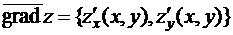 .
.
Для функции трёх переменных 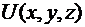 :
:
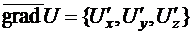 .
.
Связь градиента с производной по направлению даётся следующей теоремой.
Теорема 2. Производная функции по направлению есть проекция её градиента на это направление:
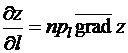 .
.
Доказательство. Проекция вектора на ось – это проекция вектора на орт оси. Проекцию же вектора на вектор можно найти, используя скалярное произведение:
 .
.
Учитывая, что 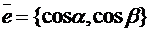 и
и 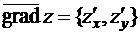 , причём
, причём 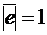 , получим:
, получим:
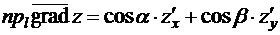 .
.
Правая часть этого равенства в силу Теоремы 1 есть производная по направле-нию. Теорема доказана.
Следствие 1. Производная функции 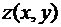 в точке
в точке 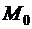 по направлению оси
по направлению оси 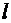 достигает максимума, когда это направление совпадает с градиентом функции, причём
достигает максимума, когда это направление совпадает с градиентом функции, причём
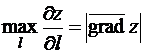 .
.
Таким образом, градиент функции в данной точке характеризует направление и величину максимальной скорости возрастания функции в данной точке.
Следствие 2. Производная функции по направлению, перпендикулярному её градиенту, равна нулю.
Метод наименьших квадратов
Евклидово пространство: точки, множества, сходимость
IТочки, множества
Определение 1. Назовем m-мерной точкой упорядоченный набор из m произвольных вещественных чисел х1, х2, … хm. Обозначения : М(х1, х2, … хm) или 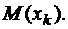 Множество всех мыслимых m-мерных точек называют m-мерным эвклидовым пространством, если расстояние между точками М(хk) и N(уk) определяется по формуле
Множество всех мыслимых m-мерных точек называют m-мерным эвклидовым пространством, если расстояние между точками М(хk) и N(уk) определяется по формуле
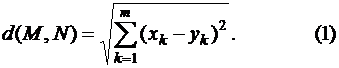

Обозначения : Rm или Em. Числа хk, k = 1,2…m, называют координатами точки М(хk), а точку О(0,0,…0) – началом координат.
Частными случаями евклидова пространства являются R2(плоскость) и R3 (обычное пространство). Формула (1) является естественным обобщением известных формул для расстояния между двумя точками на плоскости и в пространстве.
Для классификации точек и множеств в Rmважную роль играет понятие окрестности.
Определение 2. ε-окрестностью точки М0 называют множество точек вида
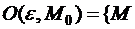
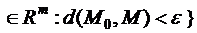 . В R1 – это интервал (x0– ε, x0+ ε), в R2 – внутренность круга, с центром в М0 и радиусом ε, а в R3 – внутренность сферы с центром в М0, и радиусом ε.
. В R1 – это интервал (x0– ε, x0+ ε), в R2 – внутренность круга, с центром в М0 и радиусом ε, а в R3 – внутренность сферы с центром в М0, и радиусом ε.
Определение 3. Точка М0 называется внутренней точкой множества G 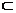 Rm, если существует ε такое, что О(ε,М0)
Rm, если существует ε такое, что О(ε,М0) 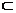 G. Точка М0 называется граничной точкой множества G, если всякая ее ε-окрестность содержит как точки, принадлежащие G, так и точки не принадлежащие G.
G. Точка М0 называется граничной точкой множества G, если всякая ее ε-окрестность содержит как точки, принадлежащие G, так и точки не принадлежащие G.
Определение 4. Множество точек называется открытым, если все его точки внутренние. Множество точек называют замкнутым, если оно содержит все свои граничные точки.
Примером открытого множества может служить ε-окрестность. Замкнутым множеством в R2 есть, например, прямоугольник {(х,у) : 0 ≤ х ≤ a, 0 ≤ y ≤ b}. Все пространство Rm и пустое множество ø являются и открытыми и замкнутыми одновременно.
Определение 5. Множество точек называется связным, если любые две его точки можно соединить непрерывной линией, которая состоит из точек данного
множества.
Например, в R2 круг – это связное множество, а множество, состоящее из двух непересекающихся кругов, не является связным.
Определение 6. Открытое связное множество называется открытой областью или, короче говоря, областью. Объединение открытой области со всеми ее граничными точками называется замкнутой областью.
Можно доказать, что замкнутая область есть замкнутое множество.
Определение 7. Множество точек G 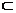 Rm называется ограниченным, если целиком содержится в некотором m-мерном “шаре”:
Rm называется ограниченным, если целиком содержится в некотором m-мерном “шаре”:
G 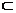 {M: d(О, M) ≤ R}.
{M: d(О, M) ≤ R}.
Ограниченными являются m-мерный “параллелипипед” (замкнутый):
{M(xk): ak ≤ xk ≤bk , k = 1,2,…m}
и m-мерный “симплекс”(открытый):
{M(xk): x1 + x2 +…+ xm< a, xk > 0,k = 1,2…m}.
Отметим для будущего, что ограниченная замкнутая область для функции нескольких переменных является аналогом замкнутого промежутка для функции одной переменной.
.
II Сходимость
Рассмотрим в Rm последовательность точек
{Mn(x1n, x2n,…, xmn)}, n = 1,2 … .
Определение 8. Говорят, что последовательность{Mn} сходится к точке М0(а1, а2,… аm) и пишут 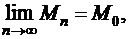 если
если 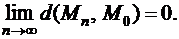
Из формулы (1),определяющейрасстояние между точками в Rm, нетрудно получить такое утверждение:
cходимость {Mn} к M0равносильна сходимости последовательностей {xkn} к аk, k = 1,2,…m. Другими словами, сходимость точек в Rm покоординатная.
Например, последовательность двумерных точек Мn 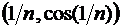 сходится к точке М0(0,1).
сходится к точке М0(0,1).
