Предел функции нескольких переменных
Непрерывность
Пусть функция 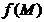 определена в некоторой окрестности
определена в некоторой окрестности 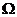 точки
точки 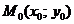 , кроме, может
, кроме, может 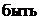 , самой точки
, самой точки 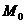 .
.
Число A называется пределом функции 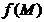 в точке в точке 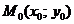 , если для любого числа , если для любого числа 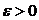 существует число существует число 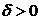 такое, что для всех точек такое, что для всех точек 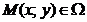 , отличных от точки , отличных от точки 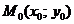 и удовлетворяющих условию и удовлетворяющих условию 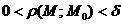 , верно неравенство , верно неравенство 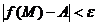 . Обозначения: . Обозначения: 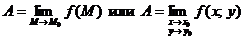 . . |
Предполагается, что точка M может стремиться к точке 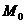 по любому
по любому 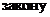 , по любому направлению, и все соответствующие предельные значения существуют и равны числу A.
, по любому направлению, и все соответствующие предельные значения существуют и равны числу A.
1. Функция 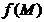 называется непрерывной в точке называется непрерывной в точке 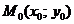 , если , если 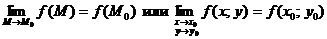 . 2. Функция . 2. Функция 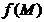 называется непрерывной в точке называется непрерывной в точке 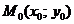 , если , если 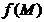 называется непрерывной в точке называется непрерывной в точке 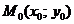 , если для всякого , если для всякого 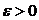 существует существует 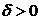 такое, что для всех точек такое, что для всех точек 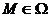 , таких, что , таких, что 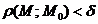 , выполняется неравенство , выполняется неравенство 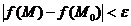 . 3. Обозначая . 3. Обозначая 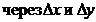 приращения независимых переменных x и y при переходе от точки приращения независимых переменных x и y при переходе от точки 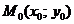 к точке к точке 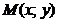 , получим, что равенство , получим, что равенство 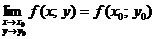 будет равносильно равенству будет равносильно равенству 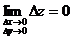 , которое означает, что бесконечно малому расстоянию между точками , которое означает, что бесконечно малому расстоянию между точками 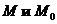 соответствует бесконечно малое приращение функции. соответствует бесконечно малое приращение функции. |
Если функция 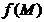 непрерывна в каждой точке области E, то она называется непрерывной в областиE. Точки, в которых функция
непрерывна в каждой точке области E, то она называется непрерывной в областиE. Точки, в которых функция 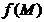 не является непрерывной, называются точками разрыва этой функции. Точки разрыва функции
не является непрерывной, называются точками разрыва этой функции. Точки разрыва функции 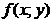 могут быть изолированными и могут заполнять целые линии.
могут быть изолированными и могут заполнять целые линии.
Частные производные и
Полный дифференциал функций нескольких переменных
Частной производной функции 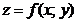 по переменной xв точке по переменной xв точке 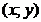 называется предел (если он существует) отношения соответствующего частного приращения функции называется предел (если он существует) отношения соответствующего частного приращения функции 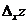 к вызвавшему его приращению независимой переменной к вызвавшему его приращению независимой переменной 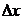 , когда , когда 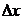 стремится к нулю. Обозначение: Обозначается частная производная любым из символов стремится к нулю. Обозначение: Обозначается частная производная любым из символов 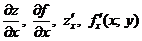 . . |
Таким образом, по определению
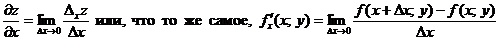 .
.
Аналогично определяется частная производная функции по переменной y:
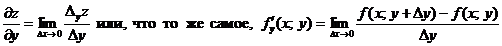 .
.
Если 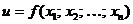 − функция n независимых переменных, то
− функция n независимых переменных, то
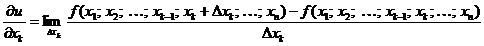 .
.



? ? ?
Заметив, что 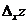 вычисляется при постоянном значении y, а
вычисляется при постоянном значении y, а 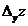 − при неизменном значении переменой x, определения частных производных можно сформулировать так:
− при неизменном значении переменой x, определения частных производных можно сформулировать так:
частной производной по переменной xфункции 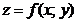 называется обычная производная этой функции называется обычная производная этой функции 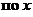 , вычисленная в предположении, что y− постоянная; частной производной по переменной yфункции , вычисленная в предположении, что y− постоянная; частной производной по переменной yфункции 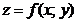 называется обычная производная этой функции называется обычная производная этой функции 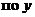 , вычисленная в предположении, что x− постоянная. , вычисленная в предположении, что x− постоянная. |
Отсюда следует, что правила вычисления частных производных совпадают с правилами, доказанными для функции одной переменной.
Замечание. Отметим одну особенность обозначения 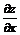 .
.
Надо помнить, что это есть цельный символ 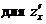 , а никак не дробь. Чем
, а никак не дробь. Чем 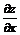 и отличается от обозначения
и отличается от обозначения  для производной функции одного аргумента
для производной функции одного аргумента 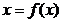 .
.
Действительно,  и в самом деле есть самая настоящая дробь. Нелишне заметить, что (в отличие
и в самом деле есть самая настоящая дробь. Нелишне заметить, что (в отличие 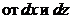 ) символы
) символы 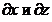 сами по себе не имеют смысла.
сами по себе не имеют смысла.



! ! !
