Теоремы о счетных множествах. Множества мощности

Континуум

Если рассмотреть любое конечное множество и любое его собственное (непустое и не совпадающее с ним самим) подмножество, то элементов в подмножестве меньше, чем в сам множестве, т. е. часть меньше целого.

Обладают ли бесконечные множества таким свойством? И может ли иметь смысл утверждение, что в одном бесконечном множестве "меньше" элементов, чем в другом, тоже бесконечном? Ведь про два бесконечных множества мы можем пока только сказать, эквивалентны они или нет. А существуют ли вообще неэквивалентные бесконечные множества?

Приведём забавную фантастическую историю из книги Н. Я. Виленкина "Рассказы о множествах". Действие происходит в далёком будущем, когда жители разных галактик могут встречаться друг с другом. Поэтому для всех путешествующих по космосу построена огромная гостиница, протянувшаяся через несколько галактик.

В этой гостинице бесконечно много номеров (комнат), но, как и положено, все комнаты пронумерованы, и для любого натурального числа n есть комната с этим номером.

Однажды в этой гостинице проходил съезд космозоологов, в котором участвовали представители всех галактик. Так как галактик тоже бесконечное множество, все места в гостинице оказались занятыми. Но в это время к директору гостиницы приехал его друг и попросил поселить его в эту гостиницу.

"После некоторых размышлений директор обратился к администратору и сказал:

– Поселите его в № 1.

– Куда же я дену жильца этого номера? – удивлённо спросил администратор.

– А его переселите в № 2. Жильца же из № 2 отправьте в № 3, из № 3 – в № 4 и т. д."

Вообще, пусть постоялец, живущий в номере k, переедет в номер k+1, как это показано на следующем рисунке:

Тогда у каждого снова будет свой номер, а № 1 освободится.

Таким образом, нового гостя удалось поселить – именно потому, что номеров в гостинице бесконечно много.

Первоначально участники съезда занимали все номера гостиницы, следовательно, между множеством космозоологов и множеством Nбыло установлено взаимно однозначное соответствие: каждому космозоологу дали по номеру, на двери которого написано соответствующее ему натуральное число. Естественно считать, что делегатов было "столько же", сколько имеется натуральных чисел. Но приехал ещё один человек, его тоже поселили, и количество проживающих увеличилось на 1. Но их снова осталось "столько же", сколько и натуральных чисел: ведь все поместились в гостиницу!

Мы пришли к удивительному выводу: если к множеству, которое равномощно N, добавить ещё один элемент, получится множество, которое снова равномощно N. Но ведь совершенно ясно, что делегаты-космозоологи представляют собой часть того множества людей, которые разместились в гостинице после приезда нового гостя. Значит, в этом случае часть не "меньше" целого, а "равна" целому!

Итак, из определения эквивалентности (которое не приводит ни к каким странностям в случае конечных множеств) следует, что часть бесконечного множества может быть эквивалентна всему множеству.

Новый постоялец не удивился, когда на другое утро ему предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить ещё 999999 жильцов.

Но потом произошла какая-то накладка, и в эту же самую гостиницу приехали на съезд филателисты. Их тоже было бесконечное множество – по одному представителю от каждой галактики. Как же их всех разместить?

Эта задача оказалась весьма сложной. Но и в этом случае нашёлся выход.

"В первую очередь администратор приказал переселить жильца из № 1 в № 2.

– А жильца из № 2 переселите в № 4, из № 3 – в № 6, вообще, из номера n – в номер 2n.

Теперь стал ясен его план: таким путём он освободил бесконечное множество нечётных номеров и мог расселять в них филателистов. В результате чётные номера оказались занятыми космозоологами, а нечётные – филателистами... Филателист, стоявший в очереди n-м, занимал номер 2n-1". И снова всех удалось разместить в гостинице. Итак, ещё более удивительный эффект: при объединении двух множеств, каждое из которых равномощно N, вновь получается множество, равномощное N, т. e. даже при "удвоении" множества мы получаем множество, эквивалентное исходному!

Определение. Множество А, равномощное множеству натуральных чисел N, называется счетным множеством(имеет мощность счетного множества). Если множество В является бесконечным и не равномощно множеству N, то его называют несчетным.

Множество, которое является конечным или счетным, еще называют не более чем счетным.

Пусть множество А является счетным. По определению, тогда существует биекция А на N, т.е. каждому аÎА соответствует единственный номер nÎN и множество А обращается в некоторую последовательность {а_n}.

Теорема 1. Любое подмножество счетного множества не более чем счетно.

Доказательство. Пусть А = {a_n} - счетное множество и В Í А. Если В конечное множество, то утверждение доказано. Предположим, что В бесконечное множество. Те элементы А, которые попали в В будут иметь некоторые номера в порядке возрастания: 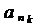. Тогда необходимая нам биекция, показывающая, что В является счетным множеством, задается в виде: 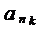® k.

Теорема 2. Объединение конечного или счетного числа счетных множеств является счетным множеством.

Доказательство. Рассмотрим счетное объединение счетных множеств (случай конечного является частным). Итак, пусть А_n - счетные множества для любого nÎN и А = È_n А_n. Для доказательства нам необходимо указать биекцию множества А на множество N, т.е. указать каждому аÎА его номер. Запишем все множества А в виде последовательностей с двумя индексами, где первый указывает номер множества. Зададим закон, который каждому элементу А ставит в соответствие некоторый порядковый номер. Если элементы множества А_n обозначить через а_nk, то высотой элемента а_nk назовем число n + k. Перепишем элементы множества А, располагая все его элементы по следующему правилу - сперва перепишем все элементы высоты 2, затем высоты 3, 4 и т.д: а₁₁, а₁₂, а₂₁, а₁₃, а₂₂, а₃₁, а₁₄, а₂₃, а₃₂, а₄₁, ... Тогда любой элемент множества А будет иметь определенный номер.

Теорема 3. Любое бесконечное множество содержит счетное подмножество.

Доказательство. Выберем в заданном множестве А какой-либо элемент, придав ему единичный индекс: а₁. Среди всех оставшихся элементов множества А найдется не равный а₁ элемент (в силу бесконечности А). Его мы обозначим через а₂. Продолжая этот процесс до бесконечности мы получим необходимое нам счетное множество {a_n} .

Теорема 4. Пусть множество М - несчетно, множество А не более чем счетно и А Í М. Тогда множество М – А равномощно множеству М.

Доказательство. Пусть множество М – А не более чем счетно. Тогда множество М = АÈ(М – А) по теореме 2 не более чем счетно. Это противоречит тому, что множество М несчетно и, следовательно, наше исходное предположение не верно. Таким образом, множество М – А несчетно. Последнее еще не означает равномощности множеств М и М – А. Докажем ее. Выделим из М – А счетное множество В. Обозначим через С множество С = (М – А) – В. Справедливы равенства М = АÈВÈС и М – А = ВÈС. Множество АÈВ счетно (теорема 2). Следовательно, существует биекция f из АÈВ на А. Теперь можно построить биекцию g из М на М – А по правилу:

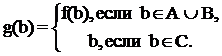
Теорема 5. Если множество С бесконечно, а В не более чем счетно, то множество ВÈС равномощно множеству С.

Доказательство. Если множество С счетно, то множество ВÈС также счетно и следовательно они равномощны. Если же множество С не счетно, то мы можем воспользоваться теоремой 4, положив в ней А = СÇВ, а М = С.

Теорема 6. Если множество С является бесконечным, то существует его подмножество В такое, что В¹С и В равномощно с С.

Доказательство. По теореме 3 мы можем выделить из множества С его счетное подмножество А. Если множество С счетно, то в качестве В из утверждения теоремы можно взять В=А. Если же С не счетно, то можно положить В=С-А и утверждаемое вытекает из теоремы 4.

Теорема 7. Множество рациональных чисел Q является счетным.

Доказательство. Обозначим через Р множество всех пар натуральных чисел (p, q), таких что p и q не имеют общих целых делителей, кроме единицы. Для пары натуральных чисел (p, q) введем ее высоту m = p + q. Обозначим Р_n множество пар натуральных чисел высоты n. Нетрудно проверить, что каждое множество Р_n является конечным и содержит не более, чем n-1 член. Так как Р = È_n Р_n, то множество Р счетно в силу теоремы 2.

Рассмотрим теперь множество Q₊ положительных рациональных чисел. Каждое положительное рациональное число представим в виде не сократимой дроби p/q. Тогда между этим числом и парами из Р существует биекция p/q « (p,q), которая показывает равномощность множеств Q ₊и Р, т.е. счетность множества Q₊. Ясно, что множества Q₊ и Q _- равномощны. Тогда Q = Q ₊ÈQ _- является счетным множеством как объединение двух счетных множеств.

Теорема 8. Множество точек интервала (0,1) является несчетным.

Доказательство(диагональный метод Кантора).Доказательство проведем от противного, предположив, что множество точек интервала (0,1) является счетным. Тогда все точки можно записать в виде последовательности:

0,а₁₁а₁₂а₁₂а₁₄ ...

0,а₂₁а₂₂а₂₃а₂₄ ...

0,а₃₁а₃₂а₃₃а₃₄ ...

0,а₄₁а₄₂а₄₃а₄₄ ...

..........................

Покажем, что на самом деле здесь записаны не все числа из интервала (0,1). Построим число 0,а₁а₂а₃а₄ ... по правилу а_k ¹ а_kk . Это всегда можно сделать. Но тогда построенное нами число входит в интервал (0,1) и не совпадает ни с одним из записанных чисел. Мы получили противоречие с тем, что нами были выписаны все числа из интервала (0,1) и этим доказали теорему.

Множества, равномощные множеству точек интервала (0, 1), называются множествами мощности континуум.

Задачи.

1. Показать, что если множества А и В являются счетными, то и их произведение А´В является счетным.

2. Установить биекцию между множеством N всех натуральных чисел и множеством Q всех четных положительных чисел.

3. Установить биекцию между множеством N всех натуральных чисел и множеством Р всех четных чисел.

Сравнение мощностей

Теорема 1 (Кантора-Бернштейна).Пусть для множеств А и В существуют множества А₁ ÍА и В₁ ÍВ такие, что множество А равномощно с В₁, а множество В с А₁, то множества А и В равномощны.

Доказательство. Пусть f - биекция В на А₁, а g - биекция А на В₁. Тогда f(В)=А₁ и f(В₁)=А₂ ÍА₁. Суперпозиция h=fog функций является также биекцией А на А₂. Тогда функция h отображает

А на А₂

А₁ Í А на А₃ Í А

А₂ Í А₁ на А₄ Í А₃

А₃ Í А₂ на А₅ Í А₆ и т.д.

Отсюда следует, что h является биекцией

из А – А₁ на А₂ – А₃

из А₁ – А₂ на А₃ – А₄

из А₂ – А₃ на А₄ – А₅ и т.д.

Зададим множества

Е = (А – А₁)È(А₂ – А₃)È(А₄ – А₅)È(А₆ – А₇)È ...

F = (А₂ – А₃)È(А₄ – А₅)È(А₆ – А₇)È ...

D = АÇА₁ÇА₂ÇА₃ÇА₄Ç...

G = (А₁ – А₂)È(А₃ – А₄)È(А₅ – А₆)È ...

Из замеченного выше следует, что h является биекцией E на F. Кроме того, справедливы равенства А = DÈGÈE и А = DÈGÈF. Следовательно отображение Т из А в А₁, определяемое соотношением

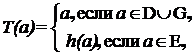
является биекцией А на А₁, т.е. множества А и А₁ равномощны. Последнее означает, что все четыре множества в теореме равномощны.

Теорема 2. Пусть Х и У два множества такие, что Х¹Æ, У¹Æ и в У не менее двух элементов. Тогда множество всех функций, действующих из Х в У является множеством, мощность которого больше мощности множества Х.

Доказательство. Обозначим множество функций, действующих из Х в У через У^Х. Доказательство разобьем на две части. Сперва покажем, что существует инъекция множества Х на часть множества У^Х. Пусть у₁ÎУ, у₂ÎУ, у₁ ¹ у₂ и х₀ÎХ. Построим функцию f[х₀] следующим образом: f[х₀](х₀) = у₁, а если х ¹ х₀, то f[х₀] (х) = у₂. При таком построении различным элементам в Х соответствуют различные функции. Например, если х₁ ¹ х₀, то f[х₁](х₀) = у₂. Таким образом, получаем инъекцию из Х в У^X.

Покажем теперь, что не существует биекции между Х и У^X. Предположим противное, что g является биекцией из Х на У^X и g(x) = f^x ÎУ^Х. Покажем, что существует fÎУ^Х такое, что f ¹ f^х для любого хÎХ. Пусть хÎХ и f^хÎУ^Х соответствующая функция. Определим f(х) = аÎУ из условия а ¹ f^х(x). Такой элемент а в У обязательно найдется, т.к. в У не менее двух элементов. Таким образом построенная функция f не будет совпадать ни с одной функцией f . Следовательно g не может быть биекцией.

Теорема 3. Множество всех подмножеств произвольного непустого множества Х имеет мощность большую, чем мощность множества Х.

Доказательство. Положим У={0,1}. Рассмотрим множество У^Х. Если fÎУ^Х, то f разбивает Х на два множества: Х₀(f) = {xÎX: f(x)=0} и Х₁(f) = {xÎX: f(x) = 1}. Таким образом, каждому fÎУ^X соответствует множество Х₁(f). Наоборот, если Х₁ - некоторое подмножество из Х, то полагая

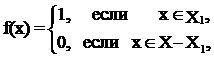
получим fÎУ^Х. Этим мы построили биекцию между множеством всех подмножеств множества Х и множеством У^Х. Следовательно они равномощны и по теореме 2 мощность множества Х меньше мощности множества всех подмножеств.

Задачи.

1. Пусть А и В произвольные конечные множества, card(А)=n, card(В)=m. Доказать, что общее число отображений из А в В равно n^m.

2. Пусть в условиях предыдущей задачи m³n. Определить число биекций и инъекций из А в В.

Примеры равномощных множеств

Приведенные выше примеры и теоремы показывают, что установить равномощность различных множеств далеко не просто. В этом параграфе мы рассмотрим примеры построения биекции между различными множествами. Будут приведены примеры доказательств равномощности ряда множеств.

Пример 1. Установить биекцию между отрезком [0, 1] и отрезком [а, в].

Решение. Легко устанавливается биективность линейного отображения x = (в – a)t + a отрезка [0, 1] на отрезок [а, в].

Пример 2. Установить биекцию между интервалом (0, 1) и интервалом (–¥, +¥).

Решение. Легко устанавливается биективность отображения x= ctg(pt) интервала (0, 1) на интервал (–¥, +¥).

Задача. Рассмотреть основные элементарные функции и найти промежутки, на которых они являются биективным отображением.

Пример 3. Построить биекцию между отрезком [0, 1] и интервалом (0, 1).

Решение. Решение этой задачи основано на несчетности рассматриваемых множеств и теореме 4 из параграфа 6. Идея решения состоит в том, что из интервала (0, 1) выделяют некоторое счетное множество А. Затем к нему добавляют две точки {0} и {1}. Вновь полученное множество (обозначим его В Ì [0, 1]), также является счетным. Следовательно, множества А и В равномощны и существует биекция f, отображающая B на A. Построим теперь биекцию отрезка [0, 1] на интервал (0, 1) следующим образом:

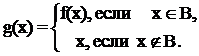
Пример 4. Построить биекцию между окружностью единичного радиуса и отрезком [0, 1].

Схема решения. Легко устанавливается биекция между точкой окружности и углом, соответствующим этой точке. Этим получается биекция окружности и полуотрезка [0, 2p). Затем по схеме примера 3 строится биекция полуотрезка [0, 2p) на отрезок [0, 1].

Пример 5. Доказать, что множество всех окружностей на плоскости, радиусы которых рациональные числа и координаты центра которых - рациональные числа, есть счетное множество.

Решение. Нетрудно видеть, что каждый элемент рассматриваемого множества может быть отождествлен с тройкой чисел (х, у, r), где (х, у) - координаты центра окружности, а r - ее радиус. Этим между множеством указанных окружностей и множеством Q´Q´Q устанавливается биекция. Но произведение счетных множеств счетно (см. задачу в 6 параграфе) и, следовательно, наше множество также счетно.

Пример 6. Доказать, что множество точек разрыва монотонной функции, заданной на отрезке [а, в], конечно или счетно.

Решение. Предположим, что рассматриваемая функция f(х) является возрастающей. Пусть х_a точка разрыва этой функции. В силу монотонности функции и ее ограниченности ( f(а) < f(х) < f(в) ) в точке х_a будет существовать как предел слева, так и предел справа: 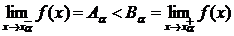Таким образом, множество точек разрыва { х_a } может быть отождествлено с множеством отрезков{[A_a , B_a]}. При этом необходимо заметить, получаемые отрезки могут пересекаться лишь на концах и все они лежат на отрезке [f(а), f(в)]. Поставим каждому отрезку [А_a, В_a] в соответствие рациональное число у_a, выбрав в качестве такового произвольное рациональное число из интервала (А_a, В_a) (наличие такое числа гарантируется аксиомой непрерывности действительных чисел и тем, что А_a ¹ В_a). В силу отмеченного выше, построенное соответствие будет являться инъекцией. Следовательно, мы построили инъекцию множества точек разрыва монотонной функции на отрезке [а, в] в счетное множество рациональных точек отрезка [f(а), f(в)]. Это означает, что рассмотренное множество точек разрыва не более чем счетно.

Задачи.

1. Существует ли функция вида 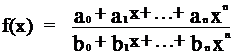(где коэффициенты a₀, a₁, ..., a_n; b₀, b₁, ..., b_n - целые числа), обладающая следующим свойством: для любого рационального числа r найдется такое целое число k, что f(k)=r.

2. Найти биекцию числовой прямой на интервал (а, в).

3. Найти биекцию полуотрезка [0, 1) на полуось [0, ¥).

4. Построить биекцию отрезка [0, 1] на всю числовую ось.

5. Существует ли непрерывная функция, являющаяся биекцией отрезка [а, в] на всю числовую ось?

6. Существует ли непрерывная функция, являющаяся биекцией отрезка [а, в] на интервал (с, d)?

7. Установить биекцию между открытым и замкнутым единичным кругом.

8. Какова мощность множества всех треугольников на плоскости, вершины которых имеют рациональные координаты?

9. Какова мощность множества всех рациональных функций с целыми коэффициентами в числителе и знаменателе?

10. Доказать, что множество точек разрыва монотонной функции, определенной на всей числовой прямой, не более чем счетно.

11. Пусть Е - счетное множество точек на прямой. Можно ли так сдвинуть это множество на величину а (т.е. заменить все точки хÎЕ точками х + а), чтобы получившееся в результате сдвига множество Е_a не пересекалось с Е?

12. Пусть Е – счетное множество точек на окружности. Можно ли повернуть окружность вокруг центра на некоторый угол j так, чтобы множество Е_j, получившееся из Е в результате поворота, не пересекалось с Е?

13. Доказать, что если расстояние между любыми двумя точками множества Е на прямой больше единицы, то множество Е не более чем счетно.

14. Какова мощность множества всех строго возрастающих последовательностей натуральных чисел?

15. Какова мощность множества всех последовательностей натуральных чисел, не содержащих число 7?

16. Какова мощность множества всех многочленов (с произвольными вещественными коэффициентами)?

17. Какова мощность множества всех отрезков на числовой прямой?

18. На числовой прямой задано множество попарно непересекающихся отрезков. Какова его мощность?

19. Какова мощность множества всех строго возрастающих непрерывных функций на отрезке [а, в]?

20. Доказать, что если А – В равномощно В – А, то А и В равномощны.

21. Доказать, что если А Í В и А равномощно АÈС, то В равномощно ВÈС.

22. Верно или нет утверждение: “Если А равномощно С, В равномощно D, причем А Ê В, С Ê D, то А – В равномощно С – D”?

23. Доказать, что множество всех конечных подмножеств счетного множества – счетно.

24. Какова мощность множества всех конечных и счетных подмножеств множества Е, если Е имеет мощность континуума?

Отношение порядка

Определение. Отношение r в множестве Х, удовлетворяющее условиям:

1) хrх для "хÎХ (рефлексивность);

2) из хrу и уrх следует, что х=у (антисимметрия);

3) из хrу и уrz следует, что хrz (транзитивность).

называется частичным порядкомна Х.

Пример. 1) Обычное отношение £ (или ³) на множестве всех чисел;

2) х является целым кратным у, где х и у из N;

3) отношение включения для множеств на множестве всех подмножеств.

Определение. Отношение r на Х, удовлетворяющее условиям:

1) хrх для "хÎХ;

2) из хrу и уrz следует хrz.

называется предпорядком.

Пример. На некотором множестве людей отношением предпорядка являются: а) рост одного человека больше или равен росту другого; б) вес одного человека больше или равен весу другого.

Если на множестве Х задано отношение предпорядка r, то полагая, что хsу, если хrу и уrх, получим отношение эквивалентности s на Х (проверить самостоятельно). Эквивалентность s разбивает Х на классы эквивалентности [x]. Обозначим через [X] - множество всех классов эквивалентности в Х. На [X] предпорядок r порождает отношение частичного порядка t по правилу [x]t[y], если $ х₁Î[x] и у₁Î[y]: x₁rу₁. Если х₂Î[x], то х₂sх₁, т.е. х₂rх₁ и х₁rу₁, следовательно, х₂rу₁. Последнее означает, что [x]t[y] тогда и только тогда, когда для "хÎ[x] и "уÎ[y] выполняется хrу. Проверьте самостоятельно, что t является отношением частичного порядка на [X].

Определение. Отношение r в Х называется строгим порядком, если это отношение обладает свойствами

1) отношение хrх не верно ни для одного хÎХ (иррефлексивность);

2) из хrу и уrz следует хrz.

Если на множестве Х задан частичный порядок r, то он порождает на Х отношение строгого порядка t по правилу: хtу тогда и только тогда, когда хrу и х¹у. Верно и обратное: отношение строгого порядка порождает отношение частичного порядка (каким образом?).

Таким образом, наличие одного из порядков, частичного или строгого, автоматически порождает на том же множестве наличие и другого порядка. Следовательно, можно говорить лишь о наличии порядка на множестве, имея ввиду, что тогда на этом множестве есть и частичный, и строгий порядки.

Множество Х, на котором введено отношение частичного порядка r, называется линейно упорядоченным (или цепью), если для "х,уÎХ выполнено одно из отношений: либо хrу, либо уrх.

Пусть Х - множество с частичным порядком r, а МÍХ. Тогда уÎХ называется левой гранью множестваМ, если уrх для "хÎМ. Если же zÎХ и хrz для "хÎМ, то z называют правой гранью множестваМ.

Определение. уÎХ называется точной левой гранью множестваМÍХ, если

1) уrх для "хÎМ;

2) zrу для "zÎХ: zrх.

Определение. уÎХ называется точной правой гранью множестваМÍХ, если:

1) хrу для "хÎМ;

2) уrz для "zÎХ: zrх.

Определение. уÎМ называется правым экстремальным (левым) элементоммножества МÍХ, если: хrу (соответственно, уrх) для "хÎМ.

Задачи.

1. Показать, что если r является отношением частичного порядка, то r^-1 также есть частичный порядок.

2. На множестве всех непрерывных функций на отрезке [а, в] введем отношение f=О(g)по определению: для всех хÎ[а, в] выполняется неравенство f(х)£Мg(х) для некоторого М. Показать, что таким образом введеное отношение является предпорядком.

3. Доказать, что отношение mµn, если n делится на m, является отношением порядка на N. Проверить, что для всякого конечного множества АÍN в этом упорядочении существует точные грани.

Элементы комбинаторики

10.1 Пусть есть некоторое конечное множество элементов U = {a₁, a₂, ..., a_n}. Рассмотрим набор элементов 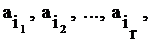, где 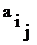ÎU, j = 1, 2, ..., r. Этот набор называется выборкойобъема r из n элементов. Любое подмножество U является выборкой, но не всякая выборка является подмножеством U, так как в выборку один и тот же элемент может входить несколько раз (в отличие от подмножества).

Комбинаторные задачи связаны с подсчетом числа выборок объема r из n элементов, где выборки подчиняются определенным условиям, т.е. выбор производится по какому-нибудь принципу. Подсчет числа выборок основывается на двух правилах теории множеств.

10.2 Принцип суммы: если card A = m, card B = n и AÇB = Æ , то card A È B = m+n. На комбинаторном языке это означает: если объект A можно выбрать m способами, объект B другими n способами и их одновременный выбор невозможен, то выбор “A или B” может быть осуществлен m+n способами.

10.3 Принцип произведения:если card A = m, card B = n, то card (A´B) = m´n. На комбинаторном языке это означает: если объект A может быть выбран m способами, при любом выборе A объект B может быть выбран n способами, то выбор “A и B” может быть осуществлен m×n способами.

10.4 Пример. A = {10 различных шоколадок}, B = {5 различных пачек печенья}. Выбор “A или B” означает, что выбирается что-то одно и способов выбора в это случае будет 15. Выбор “A и B” означает, что выбирается 1 шоколадка и 1 пачка печенья и различных вариантов для такого выбора будет 50.

10.5 Пример. Бросают 2 игральные кости. Сколькими способами они могут выпасть так, что на каждой кости выпадет четное число очков либо на каждой кости выпадет нечетное число очков ?

Пусть m - число возможностей для выпадения четного числа на одной кости, n - число возможностей для выпадения нечетного числа. Здесь m = n = 3. По правилу произведения количество выпадения четных чисел, равно как и нечетных, равно 9. По правилу суммы количество возможностей для выпадения двух четных или двух нечетных чисел будет 18.

Рассмотрим основные способы формирования выборок.

10.6 Определение.Выборка называется упорядоченной,если в ней задан порядок следования элементов. Если порядок следования элементов несущественен, то выборка называется неупорядоченной.

Из определения следует, две упорядоченные выборки, состоящие из одних и тех же элементов, но расположенных в разном порядке, являются различными.

10.7 Перестановки. Упорядоченные выборки объемом n из n элементов, где все элементы различны, называются перестановкамииз n элементов. Число перестановок из n элементов обозначается P_n.

10.8 Теорема. P = n !

Доказательство проводится по индукции. Очевидно, если n = 1, то перестановка только одна и P₁ = 1!. Пусть для n = k теорема верна и P_k = k !, покажем, что она тогда верна и для n = k + 1. Рассмотрим (k+1)-ый элемент, будем считать его объектом A, который можно выбрать k+1 способами. Тогда объект B - упорядоченная выборка из оставшихся k элементов по k. B соответствии с индуктивным предположением объект B можно выбрать k! способами. По принципу произведения выбор “A и B” можно осуществить k!´(k + 1) = (k + 1)! способами. А совместный выбор “A и B” есть упорядоченная выборка из k + 1 элементов по k + 1.

10.9 Пример. Сколько существует способов, чтобы расположить на полке 10 различных книг ? Ответ: 10 !

Можно рассуждать иначе. Выбираем первый элемент, это можно сделать n способами. Затем выбираем второй элемент, это можно сделать (n - 1) способами. По правилу произведения упорядоченный выбор двух элементов можно осуществить n´(n - 1) способами. Затем выбираем третий элемент, для его выбора останется n - 2 возможности, последний элемент можно выбрать единственным способом. Мы вновь приходим к формуле: n(n - 1)( n - r) ... 1.

10.10 Размещения. Упорядоченные выборки объемом m из n элементов (m < n), где все элементы различны, называютсяразмещениями. Число размещений из n элементов по m обозначается .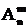

10.11 Теорема. =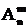

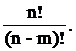
Доказательство. Обозначим x = 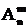. Тогда оставшиеся (n - m) элементов можно упорядочить (n - m) ! способами. По принципу произведения, если объект A можно выбрать x способами, объект B (n - m)! способами, то совместный выбор “A и B” можно осуществить x ×(n - m)! способами, но выбор “A и B” есть перестановка и P_n = n ! Отсюда x = =

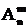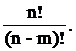
Рассуждая иначе: первый элемент выбираем n способами, второй - (n - 1) способами и т.д. , m - ый элемент выбираем (n - m + 1) способом. По принципу произведения вновь имеем: n(n - 1)...(n - m +1), что совпадает с .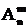

10.12 Пример. Группа из 15 человек выиграла 3 различные книги. Сколькими способами можно распределить эти книги среди группы ?

Имеем 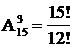= 15 ×14 ×13 = 2730.

10.13 Сочетания. Неупорядоченные выборки объемом m из n элементов (m < n) называются сочетаниями. Их число обозначается .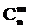

10.14 Теорема.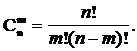

Доказательство. Очевидно, 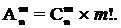Действительно, объект A - неупорядоченная выборка из n элементов по m, их число 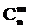. После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “ порядок “ в выборке). Совместный выбор “A и B“ - упорядоченная выборка.

10.15 Пример. Группа из 15 человек выиграла 3 одинаковые книги. Сколькими способами можно распределить эти книги?

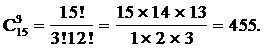
Сочетания, размещения и перестановки являлись подмножествами исходного множества. Рассмотрим выборки, которые не являются подмножествами.

10.16 Размещения с повторениями. Упорядоченные выборки объемом m из n элементов, где элементы могут повторяться, называются размещениями с повторениями. Их число обозначается 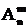(n).

10.17 Теорема. 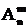(n) = n^m.

Доказательство. Первый элемент может быть выбран n способами, второй элемент также может быть выбран n способами и так далее, m -тый элемент также может быть выбран n способами. По принципу произведения получаем n^m .

10.18 Пример. Кодовый замок состоит из четырех разрядов, в каждом разряде независимо от других могут быть выбраны цифры от 0 до 9. Сколько возможных комбинаций?

Здесь n = 10, m = 4 и ответом будет 10⁴.

10.19 Пример. Рассмотрим вектор длины m, каждая координата которого может принимать всего 2 значения: 0 или 1. Сколько будет таких векторов ?

Это есть выборка объемом m из двух элементов. Ответ : 2^m

10.20 Перестановки с повторениями. Пусть имеется n элементов, среди которых k₁ элементов первого типа, k₂ элементов второго типа и т.д., k_s элементов s-того типа, причем k₁ + k₂ + ... + k_s = n. Упорядоченные выборки из таких n элементов по n называются перестановками с повторениями, их число обозначается С_n(k₁, k₂, ..., k_s). Числа С_n(k₁, k₂, ..., k_s) называются полиномиальными коэффициентами.

10.21 Теорема. С_n(k₁, ..., k_s) =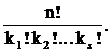

Доказательство проведем по индукции по s, то есть по числу типов элементов. При s = 1 утверждение становится тривиальным: k₁ = n, все элементы одного типа и С_n(n) = 1. В качестве базы индукции возьмем s = 2, n = k₁ + k₂. В этом случаем перестановки с повторениями превращаются в сочетания из n элементов по k₁ (или k ₂): выбираем k₁ место, куда помещаем элементы первого типа.

С_n(k₁ k₂) =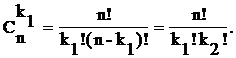

Пусть формула верна для s = m , т.е. n = k₁ + ... + k_m и

С_n(k₁, ..., k_m)=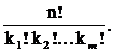

Докажем, что она верна для s = m + 1 (n = k₁ +... + k_m + k_m+1). В этом случае перестановку с повторениями можно рассматривать как совместный выбор двух объектов: объект A - выбор k _{m + 1} места для элементов (m + 1)-го типа; объект B - перестановка с повторениями из (n - k_m+1) элементов. Объект A можно выбрать 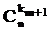способом, B - 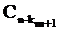(k₁, ..., k_m) способами. По принципу произведения

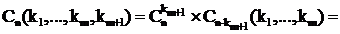
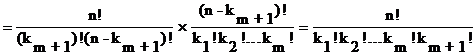
и мы получили требуемую формулу.

Замечание. Числа 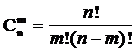называются биноминальными коэффициентами. Из этой формулы следует, что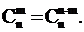

10.22 Пример. Сколько различных слов можно получить, переставляя буквы в слове “математика”?

Решение. Буква “а” входит 3 раза (k ₁= 3), буква “м” - 2 раза (k₂ = 2), “т”-2 раза ( k₃ = 2), буквы “е”,”к”,”и” входят по одному разу, отсюда k₃ = k₄ = k₅ = 1.

С₁₀ (3, 2, 2, 1, 1, 1) = 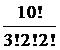=151200.

10.23 Сочетания с повторениями. Пусть имеется n типов элементов, каждый тип содержит не менее m одинаковых элементов. Неупорядоченная выборка объемом m из имеющихся элементов (их число ³ m´n ) называется сочетанием с повторениями. Число сочетаний с повторениями обозначается 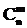(n).

10.24 Теорема. 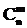(n) = .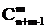

Доказательство.Пусть в выборку вошло m₁ элементов первого типа, m₂ элементов вторго типа, ... m_n - n - ного типа. Причем каждое 0 £ m_i £ m и m₁ + m₂ + ... + m_n = m. Сопоставим этой выборке вектор следующего вида:

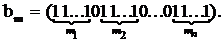
Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов {b_m} существует биекция (докажите это!). Следовательно, 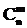(n) равно числу векторов b_m. “ Длина вектора” b_m равна числу нулей и единиц, или m + n - 1.

Число векторов равно числу способов, которыми m е