Методические указания по теме

Кафедра высшей математики

и программного обеспечения ЭВМ

Методические рекомендации к выполнению расчетно-графического задания по теме

«Аналитическая геометрия»

.

Мурманск

2009 г.

Составители – Мостовская Любовь Григорьевна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ;

Великая Елена Евгеньевна, старший преподаватель кафедры высшей математики и программного обеспечения ЭВМ МГТУ.

Хохлова Людмила Ивановна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

Методические рекомендации рассмотрены и одобрены кафедрой ВМ и ПО ЭВМ 5 февраля 2008 г., протокол № 4

Рецензент – Кацуба В.С., канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

ÓМурманский государственный технический университет, 2008

Введение. 3

Методические указания по теме. 4

Справочный материал по теме «Аналитическая геометрия». 5

1. Декартова система координат (ДСК) на плоскости. 5

2. Полярная система координат (ПСК) 5

3. Прямая линия на плоскости. 6

4. Уравнение плоскости в пространстве. 7

5. Уравнения прямой в пространстве. 8

Примерный вариант и образец выполнения РГЗ №1. 9

Варианты РГЗ №1. 15

Рекомендуемая литература. 18

Введение

Важной формой обучения студентов и курсантов 1 курса математике является их самостоятельная работа над учебным материалом: чтение учебников, решение типовых задач с проверкой правильности решения, выполнение контрольных работ и расчетно-графических заданий.

В настоящем пособии содержатся список рекомендуемой литературы, методические указания к изучению теоретического материала и рекомендации по выполнению РГЗ по теме «Аналитическая геометрия» В результате изучения этих тем студенты и курсанты 1-го курса должны:

• освоить метод координат на плоскости и научиться решать простые геометрические задачи с использованием уравнений прямой;

• освоить метод координат в пространстве, научиться решать задачи с использованием средств аналитической геометрии.

Предлагаемое пособие включает варианты РГЗ для студентов и курсантов 1 курса, а также справочный материал, необходимый для его выполнения. Кроме того, в пособии содержится решение примерного варианта, в котором имеются ссылки на используемый справочный материал.

Методические указания по теме

«Аналитическая геометрия»

В таблице 1 приведены наименования тем в соответствии с содержанием РГЗ и ссылки на литературу по этим темам. Перед выполнением РГЗ рекомендуется изучить соответствующий теоретический материал

Таблица 1.

№ к.раб.	№ задачи	Содержание (темы)	Литература
		Декартовы координаты точек на плоскости. Расстояние между двумя точками на плоскости. Деление отрезка в данном отношении. Уравнения прямой линии на плоскости. Условия параллельности и перпендикулярности прямых и плоскостей.	[1], гл.III, § 9.1, 9.2, 10.1, 10.2, 10.3; [2], гл.3, §1-2, 5, 6
		Уравнения линий на плоскости в декартовых координатах	[1], гл.III, §10.1; [2], гл.3, § 5;
		Плоскость и прямая линия в пространстве	[1], гл.IV, § 12.1-12.6; [2], гл.9, § 11-13

Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке литературы.

Справочный материал по теме «Аналитическая геометрия»

Прямая линия на плоскости

Общее уравнение прямой на плоскости:

Ах + В у + С = 0.

Уравнение прямой с угловым коэффициентом (рис. 3):

у = k x + b. (6)

Уравнение вертикальной прямой (рис. 3):

х = а. (7)

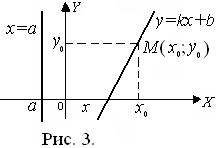Уравнения прямых, проходящих через одну заданную точку М(х₀; у_0­) (уравнение пучка прямых):

у – y₀ = k(x – x₀). (8)

Угловой коэффициент прямой, проходящей через две заданные точки А(х₁; у₁) и В(х₂; у₂):

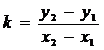. (9)

Уравнение прямой, проходящей через две заданные точки:

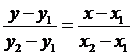. (10)

Пусть на плоскости заданы две прямые, которым соответствуют уравнения с угловыми коэффициентами: у = k₁ x + b₁ и у = k₂ x + b₂.

Условие параллельности прямых на плоскости:

k₁= k₂._. (11)

Условие перпендикулярности прямых:

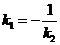. (12)

Если одна из двух перпендикулярных прямых вертикальная, т.е. k₂ не существует, то k₁= 0 и обратно: если k₂ = 0, то k₁ не существует.

Тангенс острого угла между пересекающимися прямыми можно найти, используя формулу:

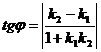, (13)

откуда 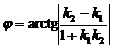. Если одна из прямых вертикальная, т.е. k₂ не существует, то .

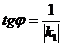Варианты РГЗ по теме

«Аналитическая геометрия»

Каждый вариант РГЗ №1 для студентов 1 курса всех специальностей содержит 4 задачи, охватывающих материал по теме «Аналитическая геометрия».

Перед выполнением РГЗ студенту необходимо изучить теоретический материал по данной теме и закрепить его решением рекомендованных задач в соответствии с методическими указаниями, затем ознакомиться со справочным материалом и образцом выполнения примерного варианта контрольной работы. Задачи 1 и 3 являются частными случаями полностью разобранных задач 2 и 4.

Cтуденту следует выбрать из условия каждой задачи данные, необходимые для ее решения, в соответствии со своим вариантом. Оформление РГЗ должно соответствовать установленным правилам и требованиям. Необходимые чертежи должны выполняться четко, с соответствующими подписями и комментариями (см. образец выполнения примерного варианта работы).

Варианты РГЗ №1

ВАРИАНТ 1

1. Даны три вершины трапеции ( 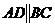): А(-3,-3), В(-2,1), С(1,2). Составить уравнение и длину высоты, проведенной из точки B на AD.

2. Даны координаты вершин треугольника АВС: А(–3;–1), В(4;6),С(8;–2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3. Составить уравнения прямой, проходящей через начало координат перпендикулярно векторам 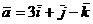и .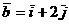

4. Заданы координаты точек– вершин пирамиды ABCD: А(6;5;8), В(3;5;8), С(8;4;1), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 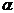между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол 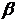между ребрами AB и BC; 8) найти угол 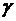между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 2

1. Даны три вершины параллелограмма ABCD: А(-3,-2), В(-2,1), С(1,2). Составить уравнение и длину высоты, проведенной из точки B на AD.

1. Даны вершины треугольника: А( -3,2), В( 4, -1), С(8,-7). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.
2. Составить уравнения прямой, проходящей через точку М(3,- 2,-1 ) параллельно вектору .
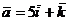3. Заданы координаты точек– вершин пирамиды ABCD: М(2,-1,0), А(3,-1,2), В(4,-1,-1), С(2,0,2). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 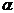между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол 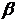между ребрами AB и BC; 8) найти угол 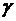между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 3

1) Даны вершины треугольника: А(1,3), В(5, 1), С(-3,-1). Найти уравнение средней линии треугольника 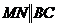и расстояние от вершины A до MN.

2) Даны координаты вершин треугольника АВС: А(–3;–2), В(4;3),С(8;6). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Найти точку пересечения прямой L: 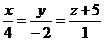с плоскостью y + 5z + 1 = 0.

4)Заданы координаты точек–вершин пирамиды ABCD: А(4,10,9), В(5,7,4), С(5,2,6), Д(1,8,2). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 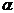между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол 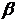между ребрами AB и BC; 8) найти угол 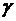между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 4

1) Даны три вершины параллелограмма: А(-4,1), В(-2 , -1), С( 2 ,-1). Найти уравнение и длину высоты, опущенной из вершины А на CD если .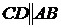

2) Даны координаты вершин треугольника АВС: А(1;–2), В(4;3),С(5;2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Составить уравнение плоскости, проходящей через точку K(2,3,-1) параллельно векторам 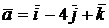и .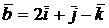

4) Даны 4 точки: М(2,0,-1), А(2,-1,1), В(0,-7,4), С(5,2,-2). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 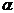между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 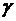между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 5

1. Даны три вершины треугольника: А(-1, -3), В(4, 2), С(4,-4). Найти точку пересечения высоты треугольника Р и ее расстояние до АВ.

2. Даны координаты вершин треугольника АВС: А(1;–2), В(4;3),С(5;2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС;

3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3. Составить геометрическое место точек, равноудаленных от плоскостей x+2y-2z-12=0 и 2x-y+2z-15=0.

4. Заданы координаты точек–вершин пирамиды ABCD: А(3,-1,2), B(4,-1,-1), C(2,0,2), А4(2,-1,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 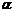между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 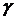между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 6

1) Даны вершины треугольника А(1;3), В(5;1), С(-3;-1). Найти уравнение средней линии треугольника (МN // ВС) и расстояние от вершины А до этой линии МN.

2) Даны координаты вершин треугольника АВС: А(1;2), В(-4;3),С(5;-2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Составить уравнения прямой, проходящей через точку Р(4,-1,3 ) параллельно вектору .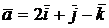

4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,0), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 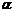между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 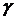между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 7

1) Даны вершины треугольника: А(0,5), В(2,-4 ), С(-5,2). Найти точку пересечения высоты треугольника 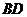и ее медианы СM.

2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Составить уравнения биссекторной плоскости, для данных плоскостей:

x+ y + 5z + 1 = 0 и 5x-y+ z+4=0.

4) Заданы координаты точек–вершин пирамиды ABCD: А(0,2,2), B(-1,-2,3),

C(4,5,-2), D(5;4;1). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 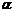между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол 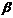между ребрами AB и BC; 8) найти угол 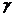между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 8

1) Даны уравнения сторон параллелограмма ABCD: АВ: x + y = 2, AD: y + 1 = 0 и точка пересечения его диагоналей Р(1,1). Найти уравнения диагоналей параллелограмма.

2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Найти проекцию точки А(2;5;1) на плоскость x+2y-3z-5=0.

4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,0), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 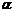между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 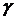между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 9

1) Даны 3 вершины трапеции А(-3;-3), В(-2;1), С(1;2). Найти уравнение основания АД(АД//ВС) и длину высоты, проведенной из вершины В.

2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Найти угол между прямой АВ и прямой 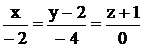, если А(4;8;0), В(7;8;2).

4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,0), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 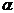между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 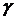между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 10

1) Даны уравнения боковых сторон равнобедренного треугольника: АВ : x - y = 0,

AС: x - 7y = 1 и точка пересечения медиан Р(2,0). Найти уравнение стороны ВС.

2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Найти угол между прямой АВ и плоскостью x-7y-2z+5=0, если А(1,9,2), В(5,1,4).

4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,0), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 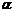между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол 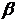между ребрами AB и BC; 8) найти угол 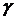между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 11

1) Даны две вершины ромба : А(-1,-4) , В(3,-1) и уравнение его диагонали BD: x + 2y - 1 = 0. Найти вершины ромба С и D.

2) Даны координаты вершин треугольника АВС: А(2;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Составить геометрическое место точек, равноудаленных от плоскостей x+2y-2z-18=0 и 2x-y+2z-15=0

4) Заданы координаты точек–вершин пирамиды ABCD: А(1,1,2), B(2,0,3), C(0,-1,2), D(2,3,4). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 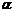между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 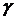между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 12

1) Даны вершины треугольника: А(1,-1), В(-2,1), C(3,-5). Найти уравнение перпендикуляра, опущенного из точки пересечения медиан треугольника на его сторону АВ.

2) Даны координаты вершин треугольника АВС: А(3;2), В(-4;3),С(5;-3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Вычислить расстояние между плоскостями x+2y-2y-6=0 и 2x+4y-4z-24=0.

4) Заданы координаты точек–вершин пирамиды ABCD: А(-1,1,3), B(2,0,3), C(0,-1,2), D(2,3,0). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 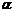между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 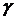между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 13

1) Даны вершины треугольника А(1;3), В(5;1), С(-3;-1). Найти уравнение средней линии треугольника (МN // ВС) и расстояние от вершины А до этой линии МN.

2) Даны координаты вершин треугольника АВС: А(–3;–1), В(4;6),С(8;–2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Составить уравнения прямой, проходящей через начало координат перпендикулярно векторам 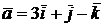и .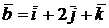

4) Заданы координаты точек– вершин пирамиды ABCD: А(-6;5;2), В(3;5;4), С(8;4;6), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 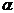между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 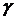между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 14

1) Даны две вершины ромба : А(-1,-5) , В(3,-3) и уравнение его диагонали BD: x + 2y - 1 = 0. Найти вершины ромба С и D .

2) Даны координаты вершин треугольника АВС: А(–4;–1), В(4;5),С(8;–3). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Составить параметрические уравнения прямой, проходящей через точку А(3;4;5) перпендикулярно векторам 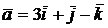и .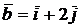

4) Заданы координаты точек– вершин пирамиды ABCD: А(6;5;8), В(3;5;8), С(8;4;1), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 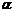между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол 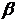между ребрами AB и BC; 8) найти угол 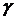между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 15

1) Даны уравнения боковых сторон равнобедренного треугольника: АВ: x - y = 0, AС: x - 7y = 1 и точка пересечения медиан Р(2,0). Найти уравнение стороны ВС.

2) Даны координаты вершин треугольника АВС: А(–3;–1), В(4;6),С(8;–2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Составить уравнения прямой, проходящей через начало координат перпендикулярно векторам 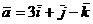и .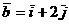

4) Заданы координаты точек– вершин пирамиды ABCD: А(6;5;8), В(3;5;8), С(8;4;1), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 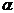между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол 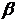между ребрами AB и BC; 8) найти угол 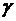между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

ВАРИАНТ 16

1) Даны три вершины трапеции ( 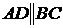): А(-3,-3), В(-2,1), С(1,2). Составить уравнение и длину высоты, проведенной из точки B на AD.

2) Даны координаты вершин треугольника АВС: А(–3;–1), В(4;6),С(8;–2). Требуется: 1) вычислить длину стороны ВС; 2) составить уравнение стороны ВС; 3) найти внутренний угол треугольника при вершине В; 4) составить уравнение высоты АК, проведенной из вершины А; 5) найти координаты центра тяжести однородного треугольника (точки пересечения его медиан); 6) сделать чертеж в системе координат.

3) Составить уравнения прямой, проходящей через начало координат перпендикулярно векторам 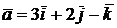и .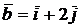

4) Заданы координаты точек – вершин пирамиды ABCD: А(-2;-5;8), В(3;4;8), С(8;4;1), Д(7;7;3). Требуется: 1)вычислить длину ребра AB; 2)найти уравнение плоскости грани ABC; 3)найти угол 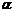между гранями ABC и BCD; 4)составить параметрические уравнения стороны AB; 5)составить канонические уравнения высоты пирамиды DK, проведенной из вершины D; 6) найти координаты точки пересечения DK и грани ABC; 7)найти угол между ребрами AB и BC; 8) найти угол 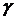между ребром AD и плоскостью ABC; 9)сделать чертеж пирамиды в системе координат.

Вопросы для самопроверки

1. Запишите формулу для вычисления расстояния между двумя точками

2. Запишитеобщее уравнение прямой на плоскости

3. Запишите уравнение прямой с угловым коэффициентом на плоскости

4. Запишите формулу для вычисления углового коэффициента прямой

5. Запишите уравнение прямой, проходящей через две заданные точки

6. Запишитеобщее уравнение плоскости

7. Запишите каноническое уравнение прямойв пространстве

8. Запишите формулу для вычисления угла между прямой и плоскостью

Рекомендуемая литература

1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М. : Айрис-пресс, 2003. – 288 с.

2. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев.– М. : Высш. шк., 1998.– 479 с.

Кафедра высшей математики

и программного обеспечения ЭВМ

Методические рекомендации к выполнению расчетно-графического задания по теме

«Аналитическая геометрия»

.

Мурманск

2009 г.

Составители – Мостовская Любовь Григорьевна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ;

Великая Елена Евгеньевна, старший преподаватель кафедры высшей математики и программного обеспечения ЭВМ МГТУ.

Хохлова Людмила Ивановна, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

Методические рекомендации рассмотрены и одобрены кафедрой ВМ и ПО ЭВМ 5 февраля 2008 г., протокол № 4

Рецензент – Кацуба В.С., канд. физ.-мат. наук, доцент кафедры высшей математики и программного обеспечения ЭВМ МГТУ

ÓМурманский государственный технический университет, 2008

Введение. 3

Методические указания по теме. 4

Справочный материал по теме «Аналитическая геометрия». 5

1. Декартова система координат (ДСК) на плоскости. 5

2. Полярная система координат (ПСК) 5

3. Прямая линия на плоскости. 6

4. Уравнение плоскости в пространстве. 7

5. Уравнения прямой в пространстве. 8

Примерный вариант и образец выполнения РГЗ №1. 9

Варианты РГЗ №1. 15

Рекомендуемая литература. 18

Введение

Важной формой обучения студентов и курсантов 1 курса математике является их самостоятельная работа над учебным материалом: чтение учебников, решение типовых задач с проверкой правильности решения, выполнение контрольных работ и расчетно-графических заданий.

В настоящем пособии содержатся список рекомендуемой литературы, методические указания к изучению теоретического материала и рекомендации по выполнению РГЗ по теме «Аналитическая геометрия» В результате изучения этих тем студенты и курсанты 1-го курса должны:

• освоить метод координат на плоскости и научиться решать простые геометрические задачи с использованием уравнений прямой;

• освоить метод координат в пространстве, научиться решать задачи с использованием средств аналитической геометрии.

Предлагаемое пособие включает варианты РГЗ для студентов и курсантов 1 курса, а также справочный материал, необходимый для его выполнения. Кроме того, в пособии содержится решение примерного варианта, в котором имеются ссылки на используемый справочный материал.

Методические указания по теме

«Аналитическая геометрия»

В таблице 1 приведены наименования тем в соответствии с содержанием РГЗ и ссылки на литературу по этим темам. Перед выполнением РГЗ рекомендуется изучить соответствующий теоретический материал

Таблица 1.

№ к.раб.	№ задачи	Содержание (темы)	Литература
		Декартовы координаты точек на плоскости. Расстояние между двумя точками на плоскости. Деление отрезка в данном отношении. Уравнения прямой линии на плоскости. Условия параллельности и перпендикулярности прямых и плоскостей.	[1], гл.III, § 9.1, 9.2, 10.1, 10.2, 10.3; [2], гл.3, §1-2, 5, 6
		Уравнения линий на плоскости в декартовых координатах	[1], гл.III, §10.1; [2], гл.3, § 5;
		Плоскость и прямая линия в пространстве	[1], гл.IV, § 12.1-12.6; [2], гл.9, § 11-13

Примечание. Ссылки на литературу в таблице даны в соответствии с номерами в списке литературы.