Теория устойчивости Ляпунова.

ОпределениеЕсли для сколь угодно малого положительного произвольного числа 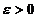найдется такое положительное число 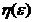такое что из условия 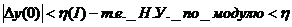следует что при t>0 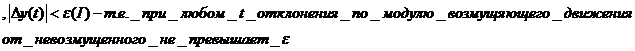невозмущенное движение будем считать устойчивым.

Если с течением времени возмущенное движение сколь угодно близко приближено к невозмущенному, то невозмущенное движение называется асимптотически устойчивым

Вывод: в линеаризованных АС устойчивость не зависит от внешних воздействий. В нелинейных системах это не так. Линейных систем не существует.

Для устойчивой замкнутой АС необходимо и достаточно чтобы вещественные части корней характеристического уравнения замкнутой АС были строго отрицательными.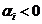

Теоремы Ляпунова

Смысл теорем Ляпунова в том, что они дают критерий, когда устойчивость линейной влечет устойчивость исходной нелинейной.

Теорема 1(об устойчиовсти): Если линеаризованная система ассимптотически устойчива, то исходная нелинейная также устойчива., если возмущенные Н.У. сколь угодны малы.

Теорема 2( о неусточивости): Если линеаризованная система неутсойчива, то исходная нелинеейная также неустойчива

Теорема 3( критический случай): Если линеаризованная система нейтрально устойчива, то для суждения о устойчивости требуется отдельное исследование системы.

Критерий устойчивости- приемы или методы исследования устойчивости без определения корней характеристического уравнения замкнутой АС. Критерии устойчивости бывают: алгебраическими и частотными

Необходимое и достаточное условие для устойчивости замкнутой АС по критерию Гурвица: необходимо и достатосно чтобы все определители Гурвица были положительными.

Необходимое и достаточное условие устойчивости по Михайлову: Для устйочивости замкнутой АС необходимо и достаточно чтобы при изменении 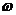Годограф:

-начинался на положительной вещественной оси( на оси х справа от нуля)

-изменялся в положительном направлении( против часовой стрелки)

-охватывать n- квадратов ( где n-порядок хар. уравнения- max степень в уравнении)

-уходить в бесконечность в n-м квадрате.

Для устойчивости замкнутой АС необходимо и достаточно чтобы корни вещественной и мнимой частей годографа чередовались

1 случай: Для устойчивости замкнутой АС. В случае устойчивой разомкнутой АС необходимо и достаточно, чтобы при изменении 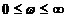Годограф КПФ разомкнутой АС (АФХ разомкнутой АС) не должен охватывать критическую точку

2случай(найквист) Для устойчивости замкнутой АС в случае нейтрально устойчивой разомкнутой АС и имеющей 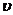интегрирующих звеньев необходимо и достаточно чтобы годограф КПФ разомкнутой АС вместе с дополнением не охватывал критическую точку.

Обобщ критерий ЦИпкина Для устойчивости Замкнутой АС в случае неустойчивой размокнутой АС необходимо и достаточно чтобы разность между числом увеличения ФЧХ и уменьшением ФЧХ на уровне -180 грудосов в области усиления (L>0) была равна m/2

Запас устойчивости-степень удаленности АС от границ устойчивости. Запас устойчивости вводится с использованием критерий устойчивости.