Построение ЛАХ и ЛФК замкнутой АС


Синтез параллельного ПКУ (кос)

По ур-ю 3 уч-к с кос приобретает св-во корректирующей обр. связи.


- . Нелинейные АС. Типовые нелинейности в автоматике.
Нелинейная автоматическая система.
АС назовем нелинейной если в ее структуру входит хотя бы 1 нелинейность.
Нелинейность – элементы АС которые имеют нелинейную статическую характеристику либо его динамика описывается нелинейным ДУ.
Покажем, что окружающий мир нелинейный.
Выход вход
U = RI R=tgα


Существует 2 случая описания реальности с помощью линейной зависимости:
1. При введении допущений (R не зависит от I)
2. В случае проведения какого либо вида линеаризации
Типовые линейности АС.
Типовые нелинейности являются идеализированными зависимостями между входной и выходной величинами.
Выделим распрастраненные и идеализированные
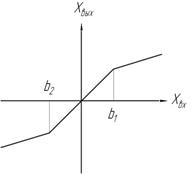 |
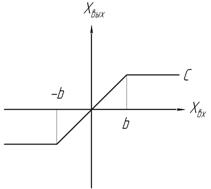 |
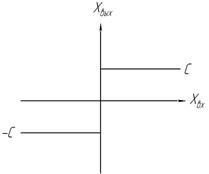 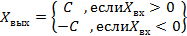 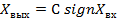 ; ; 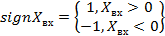 | 4. Линейность кусочная с насыщением и зоной нечувствительности 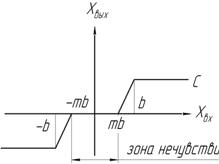 Зона нечувствительности – часть нелинейной АС, где выходной сигнал не зависит от входногоm<1 Зона нечувствительности – часть нелинейной АС, где выходной сигнал не зависит от входногоm<1 |
5. Идеальное реле с зоной нечувствительности(гистерезис запаздывает) 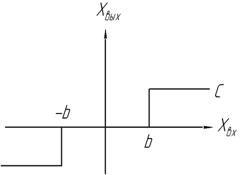 | 6. Идеальное реле с запаздыванием 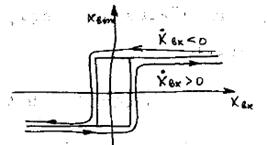 |
7. Идеальное реле с запаздыванием и зоной нечувствительности 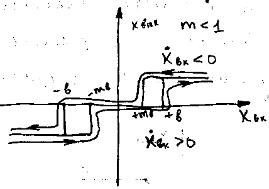 | Замечания о методах исследования нелинейных АС. Методы исследования делятся на точные и приближенные. К точным относят: 1. Классические методы решения нелинейных ДУ. Общих методов решения нелинейных ДУ не существует 2. Метод фазовой плоскости 3. Метод точечных отображений 4. Прямой метод Ляпунова Приближенные методы: 1. Аналитические (метод малого параметра, различные методы линеаризации (гармонич., эквивал. и т.д.)) 2. Численные (методы расчета на ЭВМ) |
- Особенности динамики нелинейных АС. Автоколебания, механизмы их возникновения и анализ с применением энергетических диаграмм.
Общие свойства нелинейных систем.
Свойства в переходных режимах.






 1) Показатель качества зависит от величины ступенчатого входного сигнала
1) Показатель качества зависит от величины ступенчатого входного сигнала
Вынужденные колебания в нелинейных АС
Периоды входного сигнала
В случае переходного сигнала АС
В нелинейных системах АЧХ амплитуда входного сигнала



Расщепляется (только что блять непонятно)

2) Нелинейные системы могут умножать или делить частоту входного сигнала.
При умножении колебания на выходе называются ультрагармоническими.
При делении колебания на выходе называются субгармоническими.
3) Для вынужденных колебаний характерно явление скачкообразного резонанса(рис справа вверху)
Автоколебания.
Автоколебания– самовозбуждающиеся колебания самоустанавливающиеся и самоподдерживающиеся. При этом параметры колебания зависят только от внутренних свойств системы и возникают они при отсутствии внешнего периодического воздействия.
В линейных системах автоколебания невозможны.
Существует достаточно большое количество механизмов автоколебаний. Рассмотрим 2 простейших.
Назовем энергией подкачки за период ту энергию, которая поступает в систему от источника энергии за период.
Назовем энергию, которая возникла от потерь, от сил трения, излучения, энергией десипации, или ту энергию, которая теряет нелинейная система за период колебаний.
Пример 1
Пусть имеется нелинейная система с неустойчивым положением равновесия и находится в колебательном режиме.
Известно что энергия диссипации за период, как правило, увеличивается с увеличением амплитуды колебаний.
Наступит момент, когда энергия диссипации за период станет равной энергии подкачки и амплитуда перестанет расти, т.е. наступит автоколебание.
Пример 2
Пусть имеем источник питания для нелинейной системы с насыщением по мощности и пусть имеем так же имеем нелинейную систему с неустойчивым положением равновесия и с колебательным режимом.
Амплитуда колебаний будет возрастать. Наступит момент, когда энергия подкачки будет максимальна.(ограничена)
Автоколебания удобно рассматривать на энергетических диаграммах, которые позволяют определить амплитуду колебаний и их устойчивость.
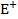 - энергия подкачки за период
- энергия подкачки за период
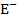 - энергия диссипации за период
- энергия диссипации за период
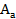 - амплитуда автоколебаний
- амплитуда автоколебаний
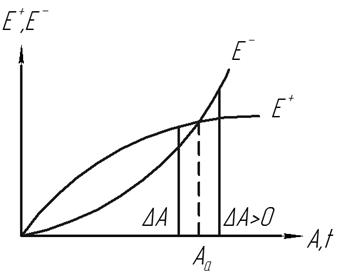
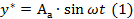
Примем (1) за невозможное движение 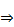 А можно считать мерой начальных условий
А можно считать мерой начальных условий
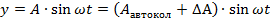 (2)
(2)
Выражение (2) это возмущенное движение
а) 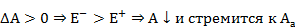
б) 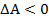
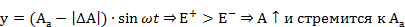 устойчива
устойчива
Кроме автоколебаний открыто новое важное свойство нелинейной системы: возникновение хаотических колебаний
В нелинейных системах устойчивость зависит от типа внешних воздействий (от вида входного сигнала или возмущения)
Вспомним доказательство которое мы делали при исследовании устойчивости нелинеаризованных АС.
Кроме того устойчивость нелинейной АС зависит от положения нелинейной системы, т.е. от начальных условий.
- Фазовое пространство и его смысл для анализа нелинейных АС. Фазовая плоскость. Свойства фазовых траекторий.
Фазовое пространство— пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.
Смысл фазового пространствава.
Пусть имеем систему вида 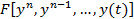 =0(1)
=0(1)
Систему 1 или ДУ назовем автоколебательной системой, т.к. в ней явно отсутствует время и внешнее воздействие.
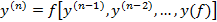 (2)
(2)
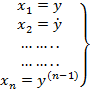 (3)
(3)
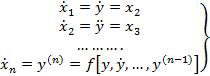 (4)
(4)
На основании 3 получим:
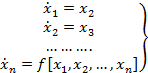 (5)
(5)
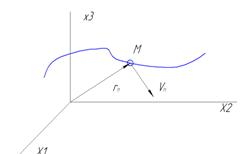
Будем трактовать 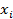 как координату некоторой точки с координатой
как координату некоторой точки с координатой 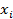
С течением времени эта точка описывает кривую, которую назовем фазовой траекторией.
Будем называть отображающей точкой М
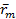 – фазовый вектор
– фазовый вектор
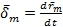 - фазовая скорость
- фазовая скорость
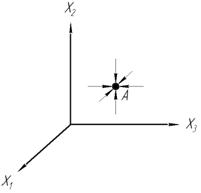 Смысл фазового пространства.По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.
Смысл фазового пространства.По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.
Пусть все фазовые траектории стягиваются в точку
Точка А является положением равновесия, причем она устойчива.
Пусть в точку А, в которую входят все траектории можно назвать аттрактор.
Положением равновесия м.б. целой областью – аттрактором.
