Кроме перечисленных вопросов необходимо владеть минимумом остаточных знаний из
Кроме перечисленных вопросов необходимо владеть минимумом остаточных знаний из
Первой части курса в виде определений и понятий: автоматическая система (АС); объект управления; регулятор, обратная связь; принцип управления по отклонению; астатическая и статическая АС; передаточная функция; переходная функция; комплексная передаточная функция; АЧХ; ФЧХ; логарифмические частотные характеристики; формулы типовых соединений звеньев; передаточные функции замкнутых АС; построение ЛАХ разомкнутых АС.
- Устойчивость в широком смысле. Примеры устойчивости и неустойчивости. Определение устойчивости по Л.М. Ляпунову. Асимптотическая устойчивость.
Устойчивость системы-способность системы сохранять свои свойства достаточно длительный промежуток времени, при действии на нее возмущающих факторов.
Это критерий физической реализуемости свойств системы а следовательно и самой системы.
Неустойчивость системы также важна
Только при неустойчивости можно получить устойчивую систему.
Важнейшим свойством действительности является движение в том числе относительный покой.
Движение АС- изменение ее выходной координаты y(t)
Невозмущенное движение-движение, для реализации которого создано АС при заданном выходном сигнале.
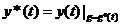 -невозмущенное(1)
-невозмущенное(1)
Всегда существуют малые причины отклонения в силу которых могут возникать большие следствия.
При устойчивости малые причины не должны вызывать больших отклонений от невозмущенного движения.
Теория устойчивости Ляпунова.
Возмущение- отклонение Н.У. от нулевых.
Любое движение, отличное от невозмущенного назовем возмущенным
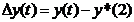 -отклонение возмущенного движения от невозмущенного.
-отклонение возмущенного движения от невозмущенного.
ð y(0)-начальное отклонение возмущенного движения от невозмущенного
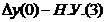
ОпределениеЕсли для сколь угодно малого положительного произвольного числа 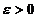 найдется такое положительное число
найдется такое положительное число 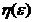 такое что из условия
такое что из условия 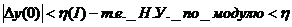 следует что при t>0
следует что при t>0 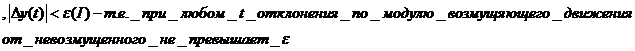 то невозмущенное движение будем считать устойчивым.
то невозмущенное движение будем считать устойчивым.
Если с течением времени возмущенное движение сколь угодно близко приближено к невозмущенному, то невозмущенное движение называется асимптотически устойчивым
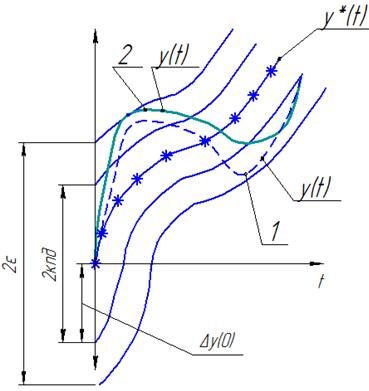
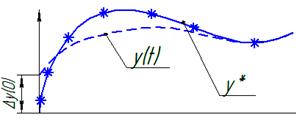
2Е-полоса возмущающего дв-я
Невозмущающ. устойчивое движениеy(t)- если для любых НУ в полосе 2кпд 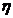
Возмущ. Дв-е не выходит из полосы 2 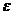
2-я неустойчивая кривая,т.к касается границы.
- Устойчивость линеаризованных АС. Условие асимптотической устойчивости линеаризованных АС. Теоремы Ляпунова об устойчивости линеаризованных АС.
Пусть имеется АС вида:
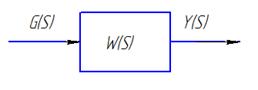
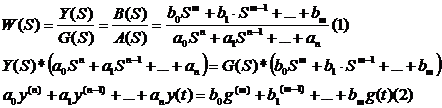
Подадим на вход АС. Сигнал 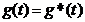 для получения на выходе желаемого сигнала и применим это движение за невозмущенное
для получения на выходе желаемого сигнала и применим это движение за невозмущенное
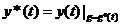 (3)
(3)
Получит 3 можно доставить g(t) в правую часть уравнения (2)
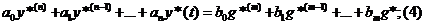
Пусть начальные условия невозмущены ( не нулевые)
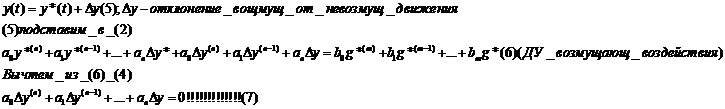
Критерий устойчивости
При высоком порядке характеристического уравнения трудно определить его корни.
Критерий устойчивости- приемы или методы исследования устойчивости без определения корней характеристического уравнения замкнутой АС. Критерии устойчивости бывают: алгебраическими и частотными
Система 1-го порядка
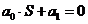
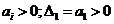
Выполнение необходимого условия влечет достаточное условие.
Система 1-го порядка всегда устойчива, если коэффициент характеристического уравнения замкнутой АС замкнут
Система 2-го порядка
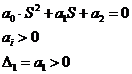
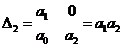
Выполнение необходимого условия влечет достаточное условие.
Система 3-го порядка
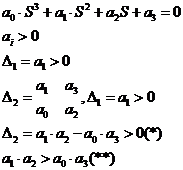
Для системы 3-го порядка необходимо чтобы произведение средних членов было больше произведения крайних
Частотные критерии устойчивости: (используются при высоком порядке хар. уравнения. Так как сложно определить знаки определителей Гурвица)
Сущность состоит в том что по виду частотных характеристик можно судить о устойчивости системы.
- Частотный критерий устойчивости Михайлова. Следствие из него (критерий чередуемости корней).
Частотные оценки
Оценка качества по АЧХ ЗАС


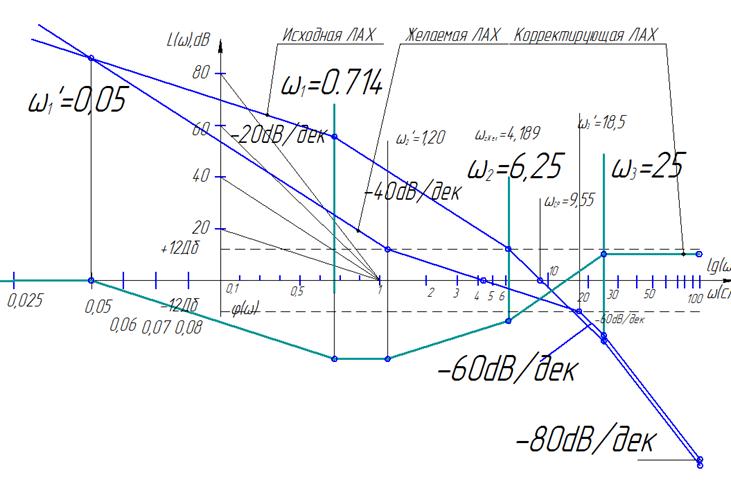
Построение ЛАХ.
Построим ЛАХ разомкнутой АС при которой АС замкнутая будет иметь желаемые качества. Существует несколько методик:
Любая желаемая ЛАХ состоит из трех участков
1. НЧ - низкочастотный участок
2. СЧ – среднечастотный участок
3. ВЧ – высокочастотный участок.
НЧ – отвечает за точность АС в статическом режиме.
СЧ – определяет запас устойчивости и основной показатель качества (время переходного процесса и 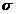 процесса).
процесса).
ВЧ – характеризует уровень помехозащищенность от ВЧ помех. В техническом задании обычно задается время регулирования 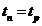 , время переходного процесса,
, время переходного процесса, 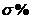 ,
, 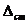 , запас устойчивости,
, запас устойчивости, 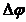 запас по фазе,
запас по фазе, 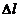 - запас по амплитуде.
- запас по амплитуде.
Кроме того в случае следящей АС задается ошибка скорости 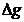 , и
, и 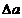 - ошибка по ускорению
- ошибка по ускорению
Если АС статич то по известной статической ошибке по отношению
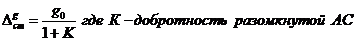 (1)
(1)
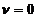 в статической АС, отсюда следует что НЧ часть это отрезок параллельный оси частот, в нашем случае лежит на уровне 20lgK, где К определяется из (1)
в статической АС, отсюда следует что НЧ часть это отрезок параллельный оси частот, в нашем случае лежит на уровне 20lgK, где К определяется из (1)
В случае следящей АС необходимо обеспечить астатизм, тогда по заданной ошибке 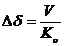 можно определить
можно определить 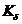 . В этом случае НЧ прямая идущая под наклоном -20 Дб на декаду.
. В этом случае НЧ прямая идущая под наклоном -20 Дб на декаду.
Построение СЧ части
СЧ имеет наклон всегда -20дб/на декаду и имеет диапазон частот не менее 1 декады. Чем больше диапазон участка тем больше запас устойчивости  в др. оно задано, выбирается для обеспечения заданного относительного перерегулирования в %:
в др. оно задано, выбирается для обеспечения заданного относительного перерегулирования в %: 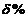
из (2) определяем 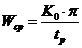 Для обеспечения заданного запаса устойчивости по амплитуде и фазе определяются границы СЧ участка.
Для обеспечения заданного запаса устойчивости по амплитуде и фазе определяются границы СЧ участка.
НЧчасть сопрягается со среднечастотной отрезком прямой с нклоном -40…-60дб/декаду. Более крутой наклон усложняет структуру корректирующего устройства.
Замечания:
1.ВЧ участок должен иметь наклон -60, -80 дб/декаду, для обеспечения высокой помехозащищенности
2. Если нужно обеспечить простую структуру корректирующего устройства то ВЧ часть проводят параллельно ЛАХ «исходной» АС. Иногда для упрощения корректирующего устройства СЧ участок продлевают так чтобы ВЧ совпадал с исходной ЛАХ.
Коррекция АС.
Для улучшения качества АС в структуру разомкнутой АС вводится специально устройство; корректирующее устройство КУ, которое бывает: последовательными, параллельными , комбинированными.
Последовательная коррекция (ПКУ) и ее особенности:
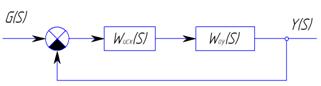
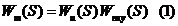 Из первого можно определить
Из первого можно определить 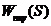
Достоинства последовательной коррекции:
1. Простота расчета
2. Простота расширения диапазона частот (полоса пропускания) путем включения в структуру разомкнутой АС деффернциирующих звеньев.
Недостатки:
1. Уменьшение надежности АС.
2. Малая мощность сигнала который может проходить через ПКУ в случае электрического 4-х полюсника.
3. Слабая помехозащищенность при включении в ПКУ дифференциирущих звеньев.
Параллельная коррекция
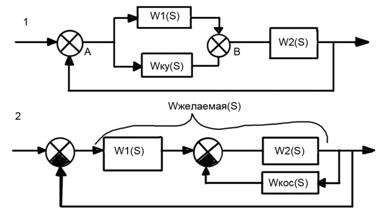
«+» параллельной коррекции
1. Возможность локального действия на элементы АС
2. Нет ограничений на мощность, передав в прямой цепи
3. Более высокая надежность по сравнению с вкл ПКУ
«-» паралельных коррекции
1. Сложность расчета
2. Сложность физической реализации
- Синтез последовательного и параллельного корректирующих устройств.
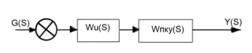
Wж(S)=Wu(S)*WПКУ(S) (1)
S=jW
Wж (jW)=Wu(jW)*WПКУ(jW) (2)
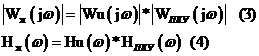
Возьмем 10-ый логарифм
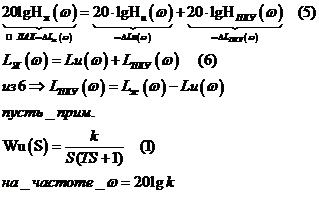


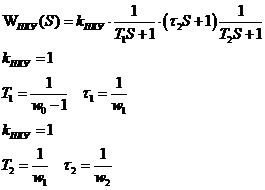
По справочнику находим элиптический 4-х полюсник.
Типовые линейности АС.
Типовые нелинейности являются идеализированными зависимостями между входной и выходной величинами.
Выделим распрастраненные и идеализированные
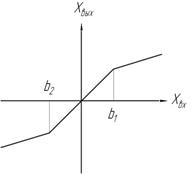 |
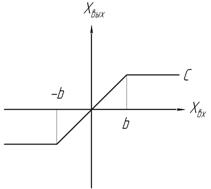 |
 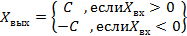 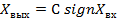 ; ; 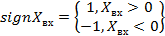 | 4. Линейность кусочная с насыщением и зоной нечувствительности 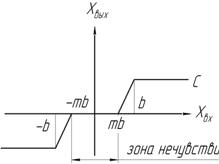 Зона нечувствительности – часть нелинейной АС, где выходной сигнал не зависит от входногоm<1 Зона нечувствительности – часть нелинейной АС, где выходной сигнал не зависит от входногоm<1 |
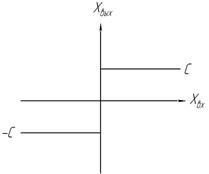
5. Идеальное реле с зоной нечувствительности(гистерезис запаздывает) 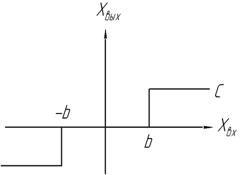 | 6. Идеальное реле с запаздыванием 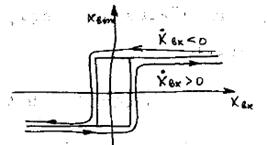 |
7. Идеальное реле с запаздыванием и зоной нечувствительности 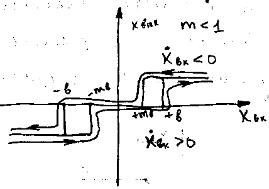 | Замечания о методах исследования нелинейных АС. Методы исследования делятся на точные и приближенные. К точным относят: 1. Классические методы решения нелинейных ДУ. Общих методов решения нелинейных ДУ не существует 2. Метод фазовой плоскости 3. Метод точечных отображений 4. Прямой метод Ляпунова Приближенные методы: 1. Аналитические (метод малого параметра, различные методы линеаризации (гармонич., эквивал. и т.д.)) 2. Численные (методы расчета на ЭВМ) |
- Особенности динамики нелинейных АС. Автоколебания, механизмы их возникновения и анализ с применением энергетических диаграмм.
Автоколебания.
Автоколебания– самовозбуждающиеся колебания самоустанавливающиеся и самоподдерживающиеся. При этом параметры колебания зависят только от внутренних свойств системы и возникают они при отсутствии внешнего периодического воздействия.
В линейных системах автоколебания невозможны.
Существует достаточно большое количество механизмов автоколебаний. Рассмотрим 2 простейших.
Назовем энергией подкачки за период ту энергию, которая поступает в систему от источника энергии за период.
Назовем энергию, которая возникла от потерь, от сил трения, излучения, энергией десипации, или ту энергию, которая теряет нелинейная система за период колебаний.
Пример 1
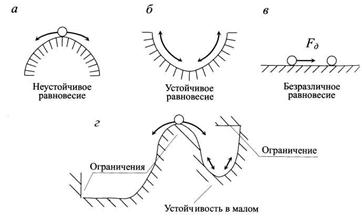
Пусть имеется нелинейная система с неустойчивым положением равновесия и находится в колебательном режиме.
Известно что энергия диссипации за период, как правило, увеличивается с увеличением амплитуды колебаний.
Наступит момент, когда энергия диссипации за период станет равной энергии подкачки и амплитуда перестанет расти, т.е. наступит автоколебание.
Пример 2
Пусть имеем источник питания для нелинейной системы с насыщением по мощности и пусть имеем так же имеем нелинейную систему с неустойчивым положением равновесия и с колебательным режимом.
Амплитуда колебаний будет возрастать. Наступит момент, когда энергия подкачки будет максимальна.(ограничена)
Автоколебания удобно рассматривать на энергетических диаграммах, которые позволяют определить амплитуду колебаний и их устойчивость.
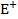 - энергия подкачки за период
- энергия подкачки за период
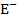 - энергия диссипации за период
- энергия диссипации за период
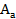 - амплитуда автоколебаний
- амплитуда автоколебаний
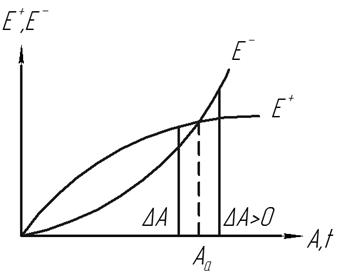
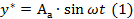
Примем (1) за невозможное движение 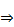 А можно считать мерой начальных условий
А можно считать мерой начальных условий
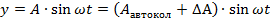 (2)
(2)
Выражение (2) это возмущенное движение
а) 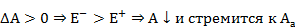
б) 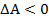
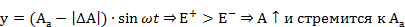 устойчива
устойчива
Кроме автоколебаний открыто новое важное свойство нелинейной системы: возникновение хаотических колебаний
В нелинейных системах устойчивость зависит от типа внешних воздействий (от вида входного сигнала или возмущения)
Вспомним доказательство которое мы делали при исследовании устойчивости нелинеаризованных АС.
Кроме того устойчивость нелинейной АС зависит от положения нелинейной системы, т.е. от начальных условий.
- Фазовое пространство и его смысл для анализа нелинейных АС. Фазовая плоскость. Свойства фазовых траекторий.
Фазовое пространство— пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.
Смысл фазового пространствава.
Пусть имеем систему вида 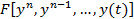 =0(1)
=0(1)
Систему 1 или ДУ назовем автоколебательной системой, т.к. в ней явно отсутствует время и внешнее воздействие.
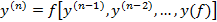 (2)
(2)
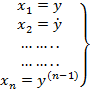 (3)
(3)
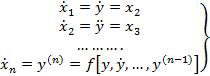 (4)
(4)
На основании 3 получим:
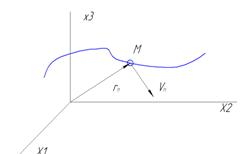
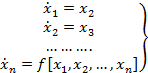 (5)
(5)
Будем трактовать 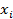 как координату некоторой точки с координатой
как координату некоторой точки с координатой 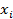
С течением времени эта точка описывает кривую, которую назовем фазовой траекторией.
Будем называть отображающей точкой М
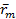 – фазовый вектор
– фазовый вектор
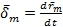 - фазовая скорость
- фазовая скорость
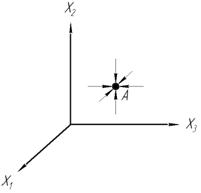 Смысл фазового пространства.По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.
Смысл фазового пространства.По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.
Пусть все фазовые траектории стягиваются в точку
Точка А является положением равновесия, причем она устойчива.
Пусть в точку А, в которую входят все траектории можно назвать аттрактор.
Положением равновесия м.б. целой областью – аттрактором.
ПФ замкнутых АС
Теоремы Ляпунова
Смысл теорем Ляпунова в том, что они дают критерий, когда устойчивость линейной влечет устойчивость исходной нелинейной.
Теорема 1(об устойчиовсти): Если линеаризованная система ассимптотически устойчива, то исходная нелинейная также устойчива., если возмущенные Н.У. сколь угодны малы.
Теорема 2( о неусточивости): Если линеаризованная система неутсойчива, то исходная нелинеейная также неустойчива
Теорема 3( критический случай): Если линеаризованная система нейтрально устойчива, то для суждения о устойчивости требуется отдельное исследование системы.
Критерий устойчивости- приемы или методы исследования устойчивости без определения корней характеристического уравнения замкнутой АС. Критерии устойчивости бывают: алгебраическими и частотными
Необходимое и достаточное условие для устойчивости замкнутой АС по критерию Гурвица: необходимо и достатосно чтобы все определители Гурвица были положительными.
Необходимое и достаточное условие устойчивости по Михайлову: Для устйочивости замкнутой АС необходимо и достаточно чтобы при изменении 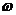 Годограф:
Годограф:
-начинался на положительной вещественной оси( на оси х справа от нуля)
-изменялся в положительном направлении( против часовой стрелки)
-охватывать n- квадратов ( где n-порядок хар. уравнения- max степень в уравнении)
-уходить в бесконечность в n-м квадрате.
Для устойчивости замкнутой АС необходимо и достаточно чтобы корни вещественной и мнимой частей годографа чередовались
1 случай: Для устойчивости замкнутой АС. В случае устойчивой разомкнутой АС необходимо и достаточно, чтобы при изменении 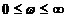 Годограф КПФ разомкнутой АС (АФХ разомкнутой АС) не должен охватывать критическую точку
Годограф КПФ разомкнутой АС (АФХ разомкнутой АС) не должен охватывать критическую точку
2случай(найквист) Для устойчивости замкнутой АС в случае нейтрально устойчивой разомкнутой АС и имеющей 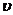 интегрирующих звеньев необходимо и достаточно чтобы годограф КПФ разомкнутой АС вместе с дополнением не охватывал критическую точку.
интегрирующих звеньев необходимо и достаточно чтобы годограф КПФ разомкнутой АС вместе с дополнением не охватывал критическую точку.
Обобщ критерий ЦИпкина Для устойчивости Замкнутой АС в случае неустойчивой размокнутой АС необходимо и достаточно чтобы разность между числом увеличения ФЧХ и уменьшением ФЧХ на уровне -180 грудосов в области усиления (L>0) была равна m/2
Запас устойчивости-степень удаленности АС от границ устойчивости. Запас устойчивости вводится с использованием критерий устойчивости.
Типовые линейности АС.
Типовые нелинейности являются идеализированными зависимостями между входной и выходной величинами.
|
|
| 4. Линейность кусочная с насыщением и зоной |
| 5. Идеальное реле с зоной нечувствительности(гистерезис запаздывает) | 6. Идеальное реле с запаздыванием |
| 7. Идеальное реле с запаздыванием и зоной нечувствительности | Замечания о методах исследования нелинейных АС. |
Автоколебания– самовозбуждающиеся колебания самоустанавливающиеся и самоподдерживающиеся.
Назовем энергией подкачки за период ту энергию, которая поступает в систему от источника энергии за период.
Назовем энергию, которая возникла от потерь, от сил трения, излучения, энергией десипации, или ту энергию, которая теряет нелинейная система за период колебаний.
Фазовое пространство— пространство, на котором представлено множество всех состояний системы, так, что каждому возможному состоянию системы соответствует точка фазового пространства.
 Смысл фазового пространства.По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.
Смысл фазового пространства.По виду фазовой траектории или по их совокупности можно судить о динамическом поведении системы.
Пусть все фазовые траектории стягиваются в точку
Точка А является положением равновесия, причем она устойчива.
Пусть в точку А, в которую входят все траектории можно назвать аттрактор.
Положением равновесия м.б. целой областью – аттрактором.
ЗАДАЧИ
- Методика определения характеристического уравнения замкнутой АС!!!
Вспомним характеристическое уравнение Замкнутой АС
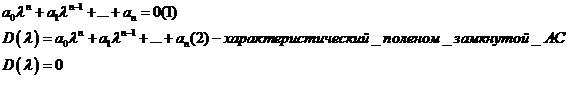
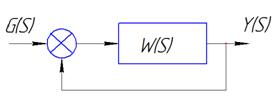 Решим задачу определения характеристического поленома замкнутой АС
Решим задачу определения характеристического поленома замкнутой АС 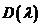
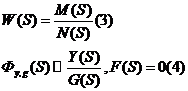

Правило 1:Определяем характеристический поленом замкнутой АС путем сложения знаменателя и числителя, как сумму числителя и знаменателя, с последующей заменой оператора АС(S) на лямбда.
N(S)+M(S)=D(S)|s=лямбда=Д(лямбда)
Правило 2: Определяем А(S)
А(S)|s=лямбда=Д(лямбда)
Правило 3:
Разрешается не заменять S на лямбда, условно считать что Sэто лямбда.
 Дляустойчивости замкнутой АС необходимо и достаточно чтобы корни характеристического уравнения лежали в левой полуплоскости на комплексной полуплоскости.
Дляустойчивости замкнутой АС необходимо и достаточно чтобы корни характеристического уравнения лежали в левой полуплоскости на комплексной полуплоскости.
ПРИМЕР:
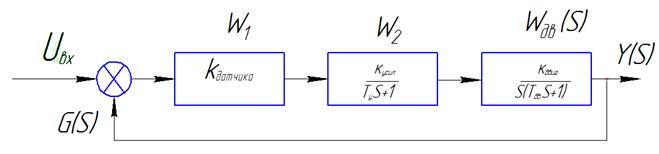
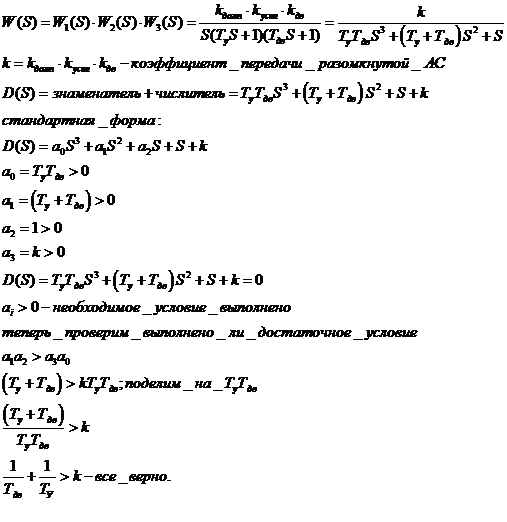
- Алгебраический критерий Гурвица
Пример:

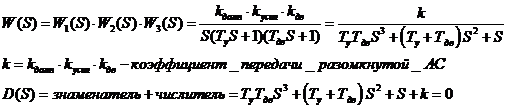
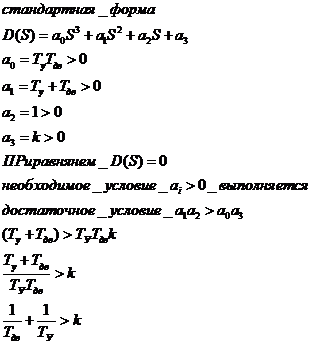
Ыыыыыы
2.2. По критерию Гурвица:
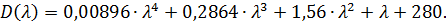
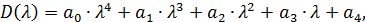
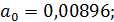
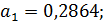
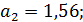
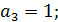
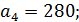
Поскольку 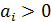 , то необходимо найти
, то необходимо найти 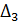 и
и 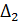 .
.
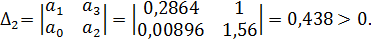
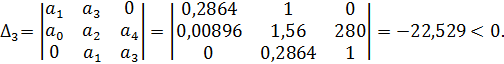
Поскольку 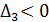 , то критерий Гурвица не выполняется и система является неустойчивой.
, то критерий Гурвица не выполняется и система является неустойчивой.
- Алгебраический критерий Михайлова
Пример:
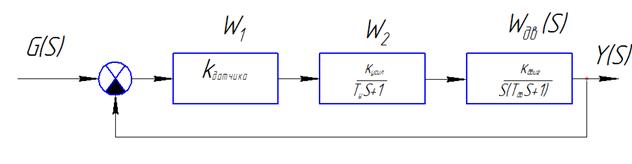
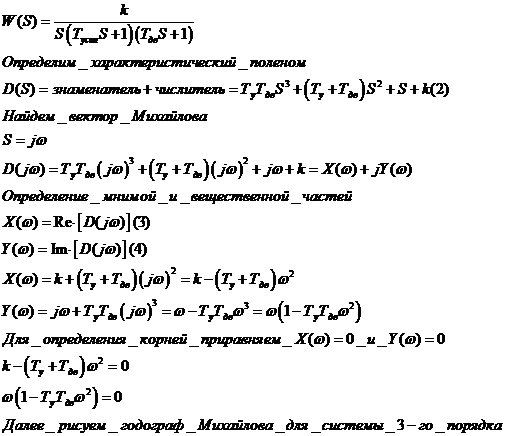
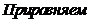
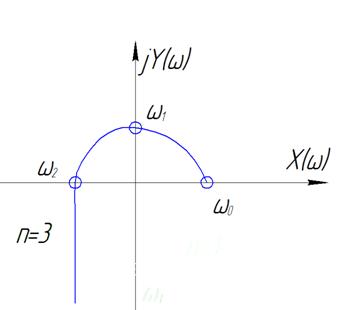
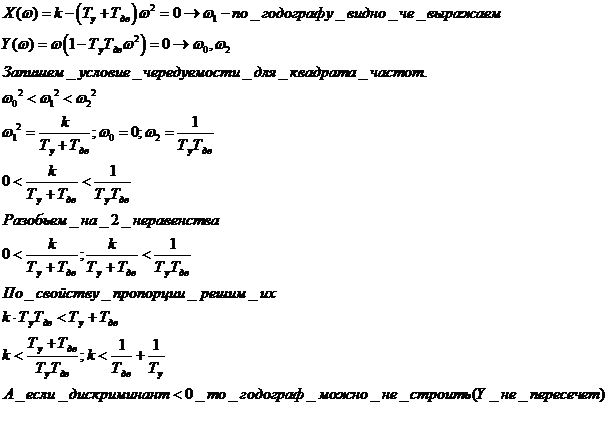
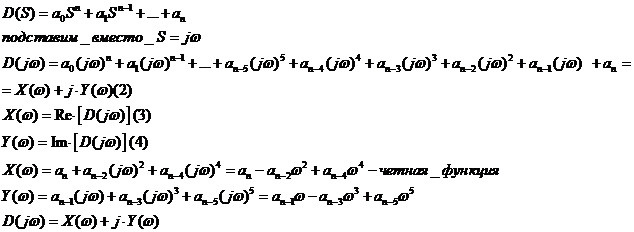
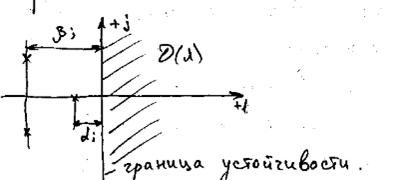
- Построение области устойчивости
правило штриховки.

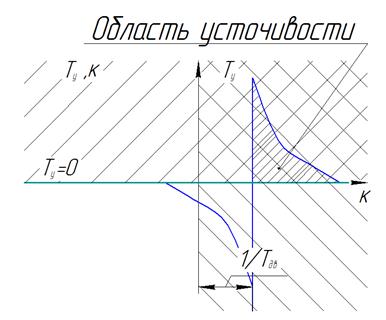
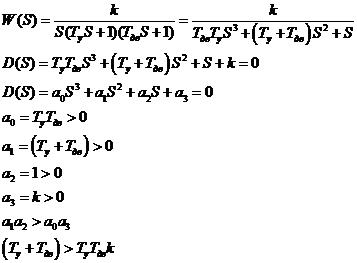
Неравенства превратим в равенство:
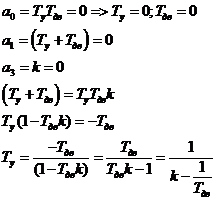
Используя необходимое условие и используя физический смысл коэффициента усиления к и Ту получим:
При определении области устойчивости используем правило штриховки.
Выразим
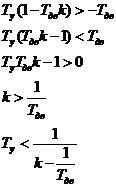
Кроме перечисленных вопросов необходимо владеть минимумом остаточных знаний из
Первой части курса в виде определений и понятий: автоматическая система (АС); объект управления; регулятор, обратная связь; принцип управления по отклонению; астатическая и статическая АС; передаточная функция; переходная функция; комплексная передаточная функция; АЧХ; ФЧХ; логарифмические частотные характеристики; формулы типовых соединений звеньев; передаточные функции замкнутых АС; построение ЛАХ разомкнутых АС.
- Устойчивость в широком смысле. Примеры устойчивости и неустойчивости. Определение устойчивости по Л.М. Ляпунову. Асимптотическая устойчивость.
Устойчивость системы-способность системы сохранять свои свойства достаточно длительный промежуток времени, при действии на нее возмущающих факторов.
Это критерий физической реализуемости свойств системы а следовательно и самой системы.
Неустойчивость системы также важна
Только при неустойчивости можно получить устойчивую систему.
Важнейшим свойством действительности является движение в том числе относительный покой.
Движение АС- изменение ее выходной координаты y(t)
Невозмущенное движение-движение, для реализации которого создано АС при заданном выходном сигнале.
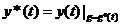 -невозмущенное(1)
-невозмущенное(1)
Всегда существуют малые причины отклонения в силу которых могут возникать большие следствия.
При устойчивости малые причины не должны вызывать больших отклонений от невозмущенного движения.
