Уравнения прямой в отрезках по осям. Угол между двумя прямыми. Расстояние от точки до прямой.
ДОПИСАТЬ
Уравнения прямой в отрезках по осям. Угол между двумя прямыми. Расстояние от точки до прямой.
1 Уравнение прямой в отрезках-это уравнение вида:
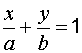
где а и в величины направленных отрезков, отсекаемых соответственно на оси Ох и Оу.
Например: написать уравнение прямой отсекаемой на осях координат отрезки, величины которых соответственно равны 3 и -5.
х\3+у\-5=1
х\3-у\5=1
у
х
-5
2Если прямые заданы общими уравнениями
A1x + B1y + C1 = 0
A2x + B2y + C2 = 0
то угол φ между ними вычисляется по формуле:
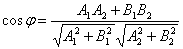(народ в знаменателе вместо б 1 квадрат нужно а 2 квадрат и вместо а 2 квадрат б 1 квадрат)
Или tg(w)=(А1В2-А2В1)\(А1А2+В1В2) –дробью
Условие перпендикулярности этих прямых имеет вид
А1А2+В1В2=0
Условие параллельности
А1\А2=В1\В2≠С1\С2
Пример:
1. Найти угол между двумя прямыми х+у-9=0 и х-6у+5=0
Тангенс фи=(1*(-6)-1*1)\(1*1+1*(-6))=7\5
Фи=арктангенс (7\5)
2. Доказать что прямые 3х-15у+16=0 и 6х-30у+13=0 параллельны
3\6=-15\-30≠16\13 следовательно параллельны
3. 30х+6у+6=0 и 6х-30у+13=0 доказать перпендикулярность
30*6+6*(-30)=0 следовательно перпендикулярны
Условия перпендикулярности и параллельности соблюдаются, т к тождества верны
3 Расстояние точки A(x1, y1) до прямой Ax + By + C = 0:
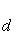
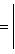
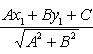
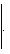
Пример:
Точка М (-2,-3) и уравнение 8х+5у+27=0
Д=(l8*(-2)+5*(-3)+27l)\корень 8 в квадрате+5 в квадрате=l-4l\корень 89=4\корень 89
Комплексные числа. Алгебраическое тригонометрическое и показательное формы комплексных чисел
Показательная форма комплексного числа
Формулой Эйлера связаны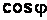 
и 
: 
.
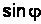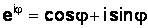Поэтому от тригонометрической формы комплексного числа можно перейти к показательной форме
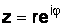. (1.7)
Тогда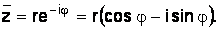 
Складывая и вычитая, легко получить
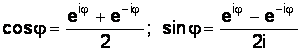. (1.8)
Пример 1.5. Записать числа из примера 4 в показательной форме.
Решение.
а)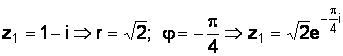 
;
б)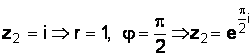 
;
в)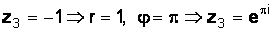 
.
Операции над комплексными числами в тригонометрической форме
Пусть
,
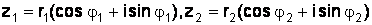тогда
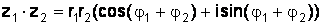; (1.13)
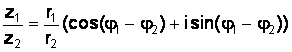. (1.14)
Пример 1.10.Дано: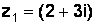 
и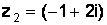 
. Найти произведение 
.
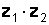Решение.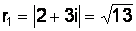 
, 
;
, 
;
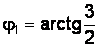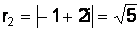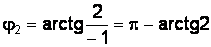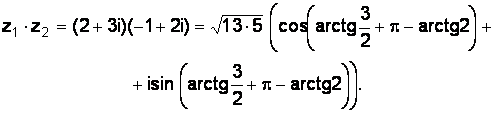
Формула Муавра: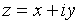 
.
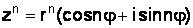; (1.15)
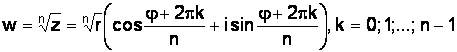; (1.16)
имеет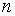 
позиций в области комплексных чисел.
Из формулы (1.16) видно, что все 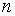различных значений величины 
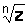имеют один и тот же модуль, равный 
. А так как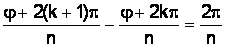 
, то точки, соответствующие значениям 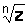, являются вершинами правильного 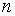-угольника, вписанного в окружность радиуса 
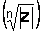, с центром в начале координат.
Пример 1.11.Найти все значения комплексно числа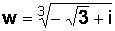 
.
Решение.
; 
; 
.
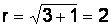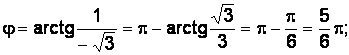
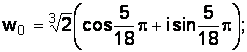
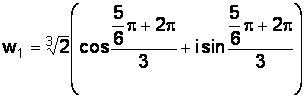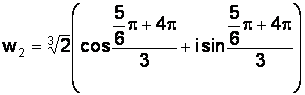Операции над комплексными числами в показательной форме.
Пусть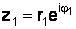 
и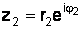 
, тогда
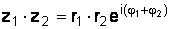; (1.17)
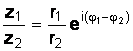; (1.18)
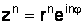; (1.19)
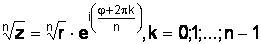. (1.20)
Пример 1.12. Вычислить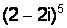 
.
Решение.
; 
;
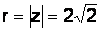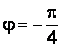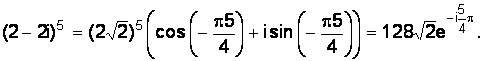
Уравнения прямой проходящей через точку, уравнения прямой проходящей через 2 точки
1. Уравнение прямой, проходящей через данную точку A(x1, y1) в данном направлении, определяемом угловым коэффициентом k,
y - y1 = k(x - x1).
Это уравнение определяет пучок прямых, проходящих через точку A(x1, y1), которая называется центром пучка.
2. Уравнение прямой, проходящей через две точки: A(x1, y1) и B(x2, y2), записывается так:
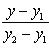
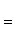
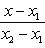
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле
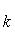
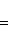
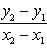
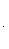
Условия перпендикулярности и параллельности соблюдаются, т к тождества верны
ДОПИСАТЬ
Уравнения прямой в отрезках по осям. Угол между двумя прямыми. Расстояние от точки до прямой.
1 Уравнение прямой в отрезках-это уравнение вида:
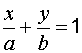
где а и в величины направленных отрезков, отсекаемых соответственно на оси Ох и Оу.
Например: написать уравнение прямой отсекаемой на осях координат отрезки, величины которых соответственно равны 3 и -5.
х\3+у\-5=1
х\3-у\5=1
у
х
-5
2Если прямые заданы общими уравнениями
A1x + B1y + C1 = 0
A2x + B2y + C2 = 0
то угол φ между ними вычисляется по формуле:
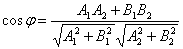(народ в знаменателе вместо б 1 квадрат нужно а 2 квадрат и вместо а 2 квадрат б 1 квадрат)
Или tg(w)=(А1В2-А2В1)\(А1А2+В1В2) –дробью
Условие перпендикулярности этих прямых имеет вид
А1А2+В1В2=0
Условие параллельности
А1\А2=В1\В2≠С1\С2
Пример:
1. Найти угол между двумя прямыми х+у-9=0 и х-6у+5=0
Тангенс фи=(1*(-6)-1*1)\(1*1+1*(-6))=7\5
Фи=арктангенс (7\5)
2. Доказать что прямые 3х-15у+16=0 и 6х-30у+13=0 параллельны
3\6=-15\-30≠16\13 следовательно параллельны
3. 30х+6у+6=0 и 6х-30у+13=0 доказать перпендикулярность
30*6+6*(-30)=0 следовательно перпендикулярны