Метод кинетостатики для материальной точки

3.7.1. Материальная точка массой m = 2 кг скользит по негладкой горизонтальной плоскости под действием силы F = 10 Н, составляющей угол α = 30° с горизонта-льной плоскостью. Определить ускорение материальной точки, если коэффициент трения скольжения f = 0,1. (3,60)

3.7.2. Груз массой m = 60 кг подвешен на нити, кото-рая наматывается на барабан (рис. 512), вращающий­ся согласно уравнению φ = 0,6 t². Определить натяжение каната, если радиус r = 0,4 м. (617)

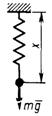
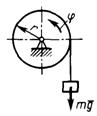
Рис. 512 Рис. 513 Рис. 514

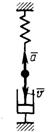
3.7.3. Материальная точка массой m = 0,6 кг колеб-лется в вертикальном направлении (рис. 513) соглас­но закону х = 25 + 3 sin 20t, где х — в см. Определить модуль реакции пружины в момент времени t = 2 с. (11,3)

3.7.4. Материальная точка массой m = 1 кг со­вершает затухающие колебания в вертикаль­ном направлении (рис. 514). В момент времени, когда ускорение точки а = 14 м/с² и скорость ее v = 2 м/с, определить реакцию пружины, если сила сопротивления демпфера 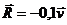. (23,6)

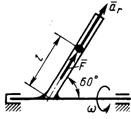3.7.5. Трубка вращается с постоянной угловой скоростью ω = 2 рад/с вокруг горизонтальной оси (рис. 515). По трубке движется материальная точка массой т = 0,2 кг с относительным ускорени­ем а_r = 4 м/с². Определить модуль силы F в момент времени, когда l = 0,2 м,

Рис. 515 а трубка находится в вертикальной

плоскости. (2,38)

Главный вектор и главный момент сил инерции

3.7.6. Тело массой 20 кг движется поступательно с ускорением 20 м/с². Определить модуль главного вектора сил инерции. (400)

3.6.7. Кривошип ОА длиной 0,1 м шарнирного парал-лелограммаОАВО₁(рис. 516) начинает вращаться из состояния покоя с постоянным угловым ускорением ε =2 рад/с². Определить модуль равнодействующей сил инер-ции стержня АВ массой 2 кг в момент времени t = 1 с. (0,894)

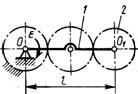
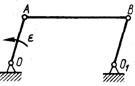
Рис. 516 Рис. 517

3.7.8. Водило 1 длиной l = 0,8 м планетарного механизма (рис. 517) вращается с постоянным угловым ускорением ε = 10 рад/с². Колесо 2 массой 2 кг при этом движется поступательно. Центр масс колеса 2 совпадает с точкой О₁. Опреде­лить главный момент сил инерции колеса 2 относительно центра О. (12,8)

3.7.9. Определить главный момент сил инерции колеса (рис. 518) относительно центра масс О, если коле­со вращается вокруг него по закону φ = 2t², а масса колеса, равная 2 кг, равномерно распределена по ободу радиуса r = 20 см. (-0,32)

3.7.10. Однородный цилиндр (рис. 519) массой 40 кг враща­ется вокруг оси Oz с угловой скоростью ω = 50t. Определить главный момент сил инер­ции цилиндра относительно оси Oz, если ради­ус цилиндра R = 0,15 м. (22,5)

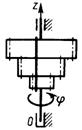
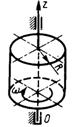
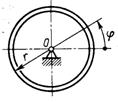
Рис. 518 Рис. 519 Рис. 520

3.7.11. Блок шестерен (рис. 520), масса которого 0,3 кг и радиус инерции ρ = 0,1 м, вращается относи­тельно оси Oz по закону φ = 25t². Определить главный момент сил инерции блока относи­тельно оси Oz. (-0,15)

3.7.12. Тонкий однородный стержень АВ массой т =1 кг (рис. 521) вращается с постоянной угловой ско­ростью ω = 5 рад/с вокруг оси, перпендику­лярной стержню. Определить модуль главного вектора сил инерции стерж-ня, если размеры l₁ = 0,2 м, l₂ = 0,4 м. (2,5)

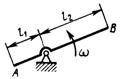
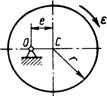
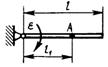
Рис. 521 Рис. 522 Рис. 523

3.7.13.Однородный тонкий стержень (рис. 522) длиной l = 1,5 м вращается с угловым ускорением ε вокруг оси, перпендикулярной стержню. Найти размер l₁, определяющий положение центра А приведения сил инерции, относительно кото­рого главный момент сил инерции равен нулю. (1)

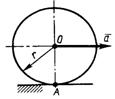
3.7.14.Определить главный момент сил инерции однородного диска (рис. 523) радиуса r = 0,2 м массой т = 2 кг относительно оси вращения О, сме­щенной на расстояние е = 0,1 м от центра масс С. Диск вращается равноускоренно с угловым ускорением ε = 10 рад/с². (0,6)

3.7.15. Однородная прямоугольная пластина (рис. 524) мас­сой 1 кг вращается с угловым ускорением ε = 30 рад/с² вокруг оси, перпендикулярной плоскости пласти-ны. Определить главный момент сил инерции относи-тельнооси враще­ния, если размер l = 0,1 м. (-0,5)

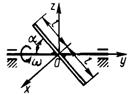
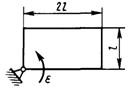
Рис. 524 Рис. 525

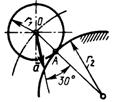
3.7.16. Тонкий однородный стержень (рис. 525) массой т = 5 кг вращается с постоянной угловой ско­ростью ω = 100 рад/с. Определить проекцию вектора главного момента сил инерции на ось Ох, если угол α = 45°, размер l = 0,25 м. (-521)

3.7.17. Однородная тонкая прямоугольная пластина (рис. 526) массой 3 кг вращается вокруг оси Oz по закону φ = 3t². Определить главный момент сил инерции пласти-ны относительно оси Oz, если размер l = 0,5 м. (1,5)

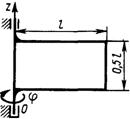
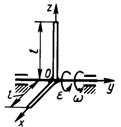
Рис. 526 Рис. 527

3.7.18. Два одинаковых однородных стержня (рис. 527) вра­щаются вокруг оси Оу, имея в данный момент времени угловую скорость ω = 10 рад/с и уг­ловое ускорение ε = 100 рад/с². Определить модуль главного вектора сил инерции стерж­ней, если масса каждого стержня 2 кг, а длина l = 0,4 м. (80)

3.7.19. Тонкая пластина (рис. 528) вращается с постоянной угловой скоростью ω = 200 рад/с. Ее центр тяжести находится на оси вращения, а центро­бежный момент инерции относительно осей в плоскости пластины равен J_xz = -2,5·10^-3 кг·м². Определить главный момент сил инерции относительно оси Оу. (-100)

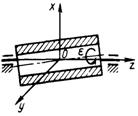3.7.20. Труба (рис. 529) вращается вокруг центральной оси Oz с угловым ускорением ε = 180 рад/с². Центробежные моменты инерции трубы равны J_xz = 1,6·10^-3 кг·м², J_yz = 0. Определить главный момент сил инерции относительно оси Ох.(0,288)

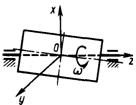
Рис. 528 Рис. 529 Рис. 530

3.7.21. Однородный цилиндр (рис. 530) радиуса r = 0,2 м катится по плоскости. Определить главный момент сил инерции относительно точки А,если масса цилиндра т = 5 кг, а ускорение его центра масс а = 4 м/с². (6)

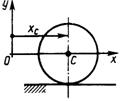
3.7.22. Однородный цилиндр (рис. 531) массой т = 10 кг катится по плоскости согласно закону х_C = 0,1 sin 0,25 πt. Определить модуль главного вектора сил инерции цилиндра в момент вре­мени t = 1 с. (0,436)

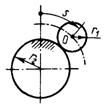3.7.23. Однородный диск (рис. 532) радиуса r₁=12 см мас­сой 10 кг катится по окружности радиуса r₂ = 20 см. Центр О диска перемещается со­гласно уравнению s = 50 rt², где s - в см. Определить модуль главного век-тора сил инер­ции диска в момент времени t = 1 с. (32,8)

Рис. 531 Рис. 532 Рис. 533

3.7.24. Однородный цилиндр (рис. 533) радиуса r₁ = 0,24 м массой 20 кг катится, по окружности радиуса r₂. Ускорение центра О цилиндра а = 60 м/с². Определить главный момент сил инерции ци­линдра, принимая за центр приведения точку А. (-216)

3.7.25. Кривошип 1 (рис. 534) вращается с постоян-ной угло­вой скоростью ω = 4 рад/с и приводит в дви­жение однородное колесо 2 массой т = 4 кг, которое катится по внутренней поверхности колеса 3. Определить модуль главного вектора сил инерции колеса 2, если радиусы R = 40 см, r = 15 см. (16)

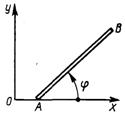
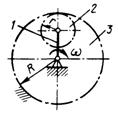
Рис. 534 Рис. 535

3.7.26. Однородный стержень (рис. 535), длина кото-рого АВ = 50 см и масса т = 10 кг, движется в плоскости Оху согласно уравнениям x_A = 4 t² , y_A = 0, φ = 6 t². Определить главный момент сил инерции стержня относительно его центра масс. (-2,5)