Дифференциальные уравнения вращательного движения тела

Дифференциальное уравнение вращательного движе-ния твердого тела имеет вид

.

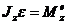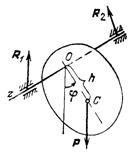
Пример 1. Исследуем движение под действием силы тяжести физического маят­ника, т. е. твердого тела, имеющего горизонтальную ось вращения (ось подвеса), не проходящую через центр тяжести те­ла (рис. 453).

Решение. Составим дифференциальное уравнение враще-ния маятника вокруг его оси подвеса:

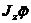= —Ph sin φ, или .

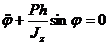Данное уравнение в элементарных функциях не интегри-руется. Для малых же углов отклонения sin φ ≈ φ, и тогда

.

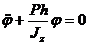Это дифференциальное уравнение свободных гармонических ко­лебаний с круговой частотой k = 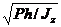и периодом .

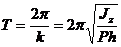Движение физического маятника

Рис. 453 при малых углах отклонения бу­дет описываться зависимостью

φ = A sin (kt + α),

где постоянные А и α определяются начальными условиями.

Определим длину l математического маятника, имеющего тот же период колебаний, что и физический. Эту длину назы-вают при­веденной длиной физического маятника. Как звестно, период малых колебаний математического маятника равен

Т = 2π .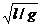

Поэтому l/g =J_я/(Ph). Отсюда получаем приведенную длину физи­ческого маятника

,

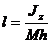где М — масса физического маятника

Задачи

3.5.1. По заданному уравнению вращения φ = 5t² - 2 пластинки, осе­вой момент инерции которой J_z = 0,125 кг·м², определить главный момент внешних сил, действующих на пластинку. (1,25)

3.5.2. Вал двигателя вращается с угловой скоростью ω = 90 е ^-20t + 85 (1 - е ^-20t ). Определить главный момент внешних сил, действу­ющих на вал, в момент времени

t = 0,1 с, если его момент инерции относительно оси вращения равен 1 кг·м². (-13,5)

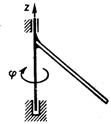
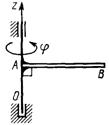
3.5.3. По заданному уравнению вращения φ = 2(t² + 1) наклонного стержня (рис. 454) с осевым моментом инерции J_z = 0,05 кг·м² опреде­лить главный момент внешних сил, действую­щих на тело. (0,2)

3.5.4. Диск (рис. 455) вращаетсявокруг оси Oz по закону φ = t³. Определить модуль момента пары сил, приложенной к диску, в момент времени t = 1 с, если момент инерции диска относитель­но оси вращения равен 2 кг·м². (12)

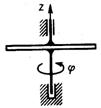
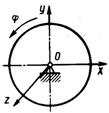
Рис. 454 Рис. 455 Рис. 456

3.5.5.По заданному уравнению вращения φ = 3 t² - t стержня (рис. 456) с осевым моментом инер­ции J_z = 1/6 кг·м² определить главный мо­мент внешних сил, дейст-вующих на стержень. (1)

3.5.6.По заданному уравнению вращения φ = t³ – 5 t²однородного цилиндра (рис. 457) радиуса R = 1,41 м, мас-сой т = 60 кг определить главный момент внешних сил, действующих на тело, в момент времени t = 2 с. (119)

3.5.7.Конус (рис. 459), масса которого т = 10 кг, а радиус основания R =1 м, вращается вокруг оси симмет-рии по закону φ = 4 sin 2 t. Определить главный момент приложенных к конусу внеш­них сил относительно оси вращения в момент времени t = π/4 с, если момент инерции кону­са J_z = 0,3mR². (- 48)

3.5.8. По заданному уравнению вращения φ = 2sin (πt/2) однородной прямоугольной пли­ты (рис. 459) с моментом инерции относительно оси вра­щения J_z = 10 кг·м² определить главный мо­мент внешних сил, действующих на тело, в момент времени t = 1 с. (- 49,3)

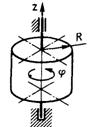
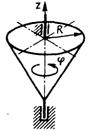
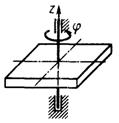
Рис. 457 Рис. 458 Рис. 459

3.5.9. Диск вращается вокруг центральной оси (рис. 460) с угловым ускорением ε = 4 рад/с² под дейст­вием пары сил с моментом М₁ и момента сил сопротивления

М₂ = 6 Н·м. Определить модуль момента М₁ пары сил, если момент инерции диска относительно оси вращения равен 6 кг·м². (30)

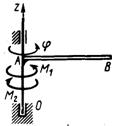
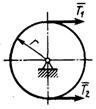
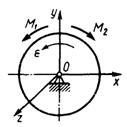
Рис. 460 Рис. 461 Рис. 462

3.5.10.Однородный стержень (рис. 461), масса кото-рого т = 2 кг и длина АВ = 1 м, вращается вокруг оси Oz под действием пары сил с моментом M₁и момента сил сопротивления M₂= 12 Н·м по закону φ = 3 t². Опреде-лить модуль момента M₁ приложенной пары сил в момент времени t = 1 с. (16)

3.5.11.Определить угловое ускорение диска (рис. 462) ради­уса r = 0,3 м массой т = 50 кг, если натяже­ния ведущей и ведомой ветвей ремня соответ­ственно равны

T₁ = 2T₂ = 100 Н. Радиус инер­ции диска относительно оси вращения равен 0,2 м. (7,5)

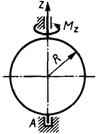
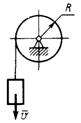
3.5.12. Определить угловое ускоре-ние однород­ного тонкого диска (рис. 463) радиуса R = 0,6 м, массой 4 кг, вращающегося вокруг вертикальной оси Az под действием момента

Рис. 463 М_z = 1,8 Н·м. (5)

3.6. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ

Работа и мощность силы

Элементарную работу силы, приложенной к материальной точке, на бесконечно малом перемещении определяют формулой

.

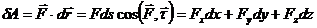Работа силы на конечном перемещении материаль-ной точки

.

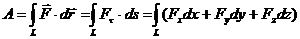Работа постоянной силы на прямолинейном участке пути s

.

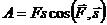Работа силы тяжести любой системы

,

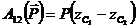где Р – сила тяжести системы; 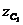и 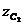- координаты центра тяжести в начальном и конечном положениях системы.

Работа упругой силы F_x = - cx при прямолинейном перемещении точки

.

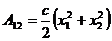Элементарную работу сил, приложенных к твердому телу, перемещающемуся произвольно, определяют по формуле

,

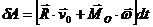где О – произвольная точка тела.

Работа сил, приложенных к твердому телу вращающемуся вокруг оси,

,

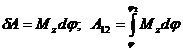где M_z – главный момент всех сил относительно оси вращения Оz.

Сумма работ всех внутренних сил в твердом теле равна нулю.

Мощность силы, приложенной в точке,

.

Мощность сил, приложенных к твердому телу,

.

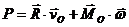Для сил, приложенных к твердому телу, вращающе-муся вокруг неподвижной оси,

Р = М_zω.

Задачи

3.6.1. Ненагруженную пружину, коэффициент жест-кости которой с = 100 Н/м, растянули на 0,02 м. Опреде-лить работу силы упругости пружины. (-0,02)

3.6.2. На тело (рис. 464) действует постоянная по

направле­нию сила F = 4х³. Определить работу этой силы при перемещении тела из положения с координатой х = 0 в положение с координатой х = 1м. (0,866)

3.6.3. Материальная точка М массой m (рис. 465) движется прямолинейно по горизонтальной плоскости по закону s = t ⁴ под действием силы F = 12 t². Определить работу этой силы при перемеще­нии ее точки

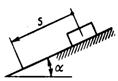приложения из начального поло­жения, где s = 0, в положение, где s = 4 м. (64)

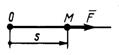
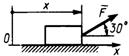
Рис. 464 Рис. 465 Рис. 466

3.6.4.Моторная лодка движется по реке со скоростью 8 м/с. Сила тяги двигателя равна 3500 Н. Определить в кВт мощность силы тяги двигателя. (28)

3.6.5. Тело скользит вниз по шероховатой плос­кости (рис.466). Зависит ли работа силы трения сколь­жения на расстоянии s от изменения угла на­клона плоскости α? (Да)

3.6.6.Однородный цилиндр массой 40 кг катится прямолинейно без скольжения по горизонтальной плоскости с угловой скоростью ω= 4 рад/с. Коэффициент трения качения δ = 0,01 м. Определить мощность сил сопротивления качению.(-15,7)

Кинетическая энергия

Кинетическая энергия материальной точки .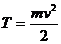

Кинетическая энергия системы п материальных точек .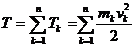

Кинетическая энергия твердого тела при поступа-тельном движении

,

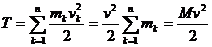где М = 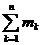- масса тела.

Кинетическая энергия твердого тела при его вращательном движении

,

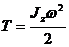где J_z – момент инерции тела относительно оси вращения, ω – угловая скорость тела.

Для общего случая движения твердого тела (в том числе и для плоского движения)

,

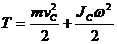где J_C – момент инерции тела относительно мгновенной оси, проходящей через центр тяжести, ω – мгновенная угловая скорость.

Задачи

3.6.7. Частота вращения рабочего колеса вентилятора равна 90 об/мин. Определить кинетическую энергию колеса, если его момент инерции относительно оси вращения равен 2,2 кг·м². (97,7)

3.6.8. Для указанного положения механизма (рис. 467) определить кинетическую энергию шатуна АВ массой т = 1 кг, если кривошип ОА длиной 0,5 м вращается вокруг оси О с угловой ско­ростью ω = 2 рад/с. (0,5)

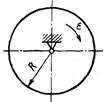
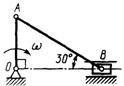
Рис. 467 Рис. 468 Рис. 469

3.6.9. Однородный диск (рис. 468) массой т = 30 кг ра­диуса R = 1 м начинает вращаться из состоя­ния покоя равноускоренно с постоянным угловым ускорением

ε = 2 рад/с². Опреде­лить кинетическую энергию диска в момент времени t = 2 с после начала движения. (120)

3.6.10. Однородный стержень (рис. 469), масса которого т = 3 кг и длина АВ = 1 м, вращается вокруг оси Oz по закону φ = 2 t³. Определить кинетическую энергию стержня в момент времени t = 1 с. (18)

3.6.11. Однородная прямоугольная пластина (рис. 470) мас­сой т = 18 кг вращается вокруг оси АВ с

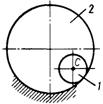
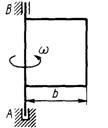
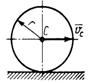
Рис. 470 Рис. 471 Рис. 472

угловой скоростью ω = 4 рад/с. Определить кинети-ческую энергию пластины, если длина b = 1 м. (48)

3.6.12. Диск массой т = 2 кг радиуса r = 1 м (рис. 471) катится по плоскости, его момент инерции относительно оси, проходящей через центр С перпен-дикулярно плоскости рисунка, J_C = 2 кг·м². Определить кинетическую энергию диска в момент времени, когда скорость его центра v_C = 1 м/с. (2)

3.6.13. Однородный цилиндр 1 (рис. 472) массой т = 16 кг катится без скольжения по внутренней цилинд­рической поверхности 2. Определить кинети­ческую энергию цилиндра в момент времени, когда скорость его центра масс С равна 2 м/с. (48)

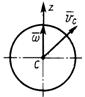
Рис. 473 Рис. 474 Рис. 475

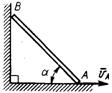
3.6.14. Однородный стержень АВ (рис. 473) длиной 2 м и массой т = 6 кг при своем движении сколь­зит конца-ми А и В по горизонтальной и верти­кальной плоскостям. Определить кинетичес­кую энергию стержня в момент времени, когда угол α = 45° и скорость точки А равна v_A= 1 м/с. (2)

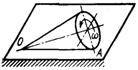
3.6.15. Прямой круговой конус (рис.474) катится без скольжения по горизонтальной плоскости, имея угловую скорость ω = 5 рад/с во враща­тельном движении вокруг мгновенной оси вращения. Момент инерции конуса относи­тельно оси ОА равен 0,04 кг·м². Определить кинетическую энергию конуса. (0,5)

3.6.16. Шар массой т = 5 кг свободно движется в пространстве (рис. 475); скорость v_r центра С шара равна 4 м/с, а его угловая скорость 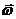враще­ния вокруг мгно-венной оси Cz равна 10 рад/с. Определить кинетическую энергию шара, если его момент инерции относительно оси Cz равен 0,5 кг·м². (65)

3.6.17. Чему равна кинетическая энергия зубчатой передачи двух цилиндрических колес с числом зубьев z₂ = 2z₁, если их момент инер­ции относительно осей вращения J₂ = 2J₁= 2 кг·м², а угловая скорость колеса 1 равна 10 рад/с. (75)

3.6.18. Четыре груза массой т = 1 кг каждый (рис. 476), соединенныегибкой нитью, переброшенной через неподвижный невесомый блок, движутся согласно закону s = 1,5t². Определить кине­тическую энергию системы грузов в момент времени t = 2 с. (72)

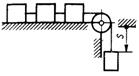
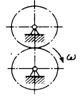
Рис. 476 Рис. 477 Рис. 478

3.6.19. Определить кинетическую энергию систе­мы (рис. 477), состоящей из двух одинаковых зубчатых колес массой т = 1 кг каждый, вращающихся с угловой скоростью ω = 10 рад/с. Радиус инерции каждого колеса относительно оси вра­щения равен 0,2 м. (4)

3.6.20. Груз массой т = 4 кг, опускаясь вниз (рис. 478), приводит с помощью нити во вращение ци­линдр радиуса R = 0,4 м. Момент инерции цилиндра относи-тельно оси вращения J = 0,2 кг·м². Определить кинети-ческую энер­гию системы тел в момент времени, когда скорость груза v = 2 м/с. (10,5)

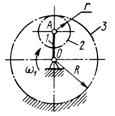3.6.21. Кривошип 1 (рис. 479), вращаясь с угловой ско­ростью ω = 10 рад/с, приводит в движение колесо 2 массой 1 кг, которое можно считать однородным диском. Момент инерции криво­шипа относительно оси враще-ния равен 0,1 кг·м². Определить кине-

Рис. 479 тическую энергию механизма, если

радиус R = 3r = 0,6 м. (17)

3.6.3. Теорема об изменении кинетической энергии механической системы

С помощью теоремы об изменении кинетической энер­гии решается как прямая, так и обратная задачи дина­мики. В дифференциальной форме теорема применяется для того, чтобы найти по заданным силам ускорения то­чек системы (или наоборот), т. е. чтобы составить диф­ференциальные уравнения движения системы и интегри­рованием этих уравнений найти законы изменения ско­ростей и перемещений точек системы. Интегральная форма теоремы используется в тех случаях, когда при конечном перемещении системы заданы три из следую­щих четырех величин: скорости, перемещения, силы, массы, а четвертая подлежит определению. Теорема ча­ще всего применяется для исследования движения меха­нических систем с одной степенью свободы, т. е. систем, положение которых определяется одной координатой (ли­нейной или угловой). Поэтому мы будем рассматривать только такие системы.

При решении задач с использованием теоремы в диф­ференциальной форме рекомендуется следующий порядок действий.

1. Выбрать координату, определяющую положение системы. Как правило, это величина, закон изменения которой (или ее производной) требуется найти. Начало отсчета данной координаты выбирается или в начальном положении системы, или в положении ее статического равновесия. Определить начальные значения координаты и ее производной по времени. Если в задаче требуется найти только ускорение, то этот пункт становится из­лишним.

2. Изобразить систему в текущий момент временя, т. е. при t > 0, дав ей смещение в сторону возрастания выбранной координаты. Построить все приложенные к системе внешние и внутренние силы (в случае неизме­няемой системы или системы твердых тел, соединенных идеальными связями, только внешние силы, так как в этом случае 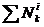= 0).

3. Записать теорему об изменении кинетической энергии в дифференциальной форме:

dT/dt = + .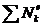

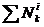4. Подсчитать кинетическую энергию в текущем положении системы, выразив ее как функцию скорости звена, движение которого требуется определить (или задано).

5. Подсчитать сумму мощностей внешних и внутрен­них сил (или сумму их элементарных работ), выразив ее как функцию скорости звена, движение которого оп­ределяется (или задано).

6. Подставить полученные значения кинетической энергии и суммы мощностей в уравнение теоремы, полу­чив таким образом дифференциальное уравнение движения системы. Если решается прямая задача, то из дан­ного уравнения найти искомую силу.

7. Проинтегрировать полученное уравнение, исполь­зуя начальные условия, и найти искомые величины.

Пример 1. Груз А массой m₁ = 1,02 кг опускаетсяпо шероховатой наклонной плоскости (коэффициент трения k = 0,2), составляющей с горизонтом угол α = 45°. К грузу А прикреплена невесомая и нерастяжимая нить, перекинутая через блок В и на­мотанная на однородный круглый цилиндр D массой т₂ = 2,04 кг и радиусом r = 0,4 м, который катится по горизонтальной плоско­сти без скольжения (рис. 480, а). Масса блока т₃ = 0,51 кг, его радиус r₁= 0,1 м, а его радиус инерции относительно оси вра­щения ρ = 0,08 м. Нить по блоку В и цилиндру D не скользит; трением в оси блока и трением качения цилиндра о плоскость мо­жно пренебречь. Найти угловое ускорение цилиндра D.

Рис. 480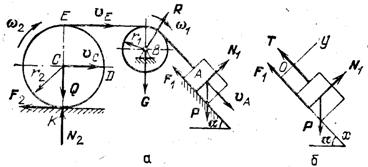

Решение. Поскольку требуется найти ускорение, для ре­шения задачи применим теорему об изменении кинетической энер­гии в дифференциальной форме:

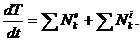
Изобразим систему вместе с действующими на нее внешними си­лами: активными ( ) и реакциями свя­зей ( 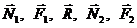). Внутренние силы не показываем, так как система состоит из твердых тел, соединенных идеальной связью (гибкой нерастяжимой нитью), и поэтому 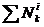= 0. Сила трения F₁ = fN₁. Чтобы найти нормальную реакцию N₁, рассмотрим дви­жение груза А, освободив его от связей и заменив их реакциями 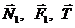; оси координат показаны на рис. 480,б. Груз совершает поступательное прямолинейное движение вдоль оси Ох, поэтому дифференциальное уравнение его движения в проекции на ось Оу дает

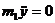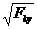, = - Pcos α + N₁

откуда N₁ = Pcos α. и, следовательно, F₁ = f P cosα .

Рассматриваемая система состоит из трех тел,А, В и D, так что ее кинетическая энергия состоит из трехслагаемых;

Т = Т_А + Т_В + Т_D.

/r_1. Тело А совершает поступательное движение, поэтому

;

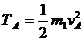блок В вращается вокруг неподвижной оси, поэтому

;

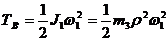цилиндр D совершает плоскопараллельное движение, поэтому

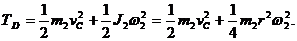
Выразим скорости v_A, ω₁, v_С через угловую скорость цилинд­ра ω, угловое ускорение которого требуется определить. Точка К цилиндра является его мгновенным центром скоростей, так что v_C = ω₂r, v_E = ω₂r₂. Нить нерастяжима, т. е. v_E = v_A и не скользит по блоку, т. е.

ω₁ = v_E/r₁ = 2ω₂r_2.

Выражение кинетической энергии системы принимает вид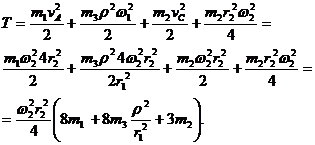

Определим мощность внешних сил, приложенных к системе (как было указано выше, мощность внутренних сил равна нулю);

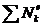= N_P + 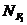= Pv_A sin α – F₁v_A =

= m₁g (sin α— f cos α) 2ω₂r₂.

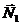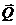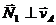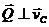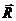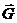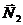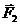Мощности нормальной реакции и силы тяжести равны нулю, так как эти силы перпендикулярны скоростям точек их приложе­ния: , ; мощности реакции и силы тяжести рав­ны нулю, так как эти силы приложены в неподвижной точке; мощности сил и равны нулю, так как они приложены в мгновенном центре скоростей.

Подставим полученные значения кинетической энергии и мощностей в формулу теоремы и опреде­лим искомое ускоре-ние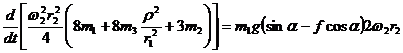

или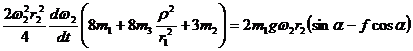

Сократив на 2ω₂r₂ и разделив обе части на коэффициент при ε₂ = dω₂/dt, получим

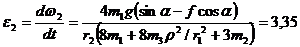рад/с².

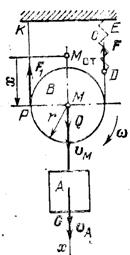
Пример 2. Груз А массой m₁ = 105 кг подвешен к подвиж­ному однородному блоку В массой т₂ = 10 кг. Блок и груз удерживаются от падения тросом, конец К которого закреплен непод­вижно, а конец D соединен с пружиной DE жесткостью

с = 1470 Н/м (рис. 481); трос по блоку не скользит. Найти период свободных колебаний системы, а так же закон движе-ния груза А,если в начальный момент система находится в положении стати­ческого равновесия и груз А имеет скорость v = 14 см/с, направленную вертикально вниз.

Решение. Для определения движения груза А надо составить дифференциальное урав­нение движения системы, и, следовательно, предпочтительнее воспользоваться теоремой об изменении кинетической энергии в дифферен­циальной форме:

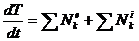
Так как система состоит из твердых тел, соеди­ненных идеальным шарниром М и нерастяжи­мым тросом, весом которого пренебрегают, сум­ма мощностей внутренних сил равна нулю:

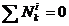
Рис. 481 Положение системы определяется положением груза А, и, следовательно, положением точки М центра блока. Предполагая, что точка М движется только по вертикали, определим ее положение координатой х, отсчитываемой от статического положе­ния центра диска (точка М_ст).

К системе приложены внешние силы: силы тяжести 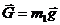, 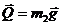и реакции связей 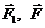. Упругая сила пружины равна F = сδ, где δ — деформация пружины, которую мы представим в виде суммы статической деформации δ_ст и деформации х_D, про­исходящей за счет смещения точки D при движении системы, так что F = с(δ_ст + хD). Когда система нахо-дится в положении ста­тического равновесия, упругая сила пру-жины (F_ст = сδ_ст) удер­живает в равновесии блок с грузом. Из соображений симметрии следует, что при этом

F_cт = F_1ст = (G + Q)/2, или G + Q = 2сδ_ст

Наша система состоит из груза А, движущегося поступа-тель­но, и блока В, совершающего плоскопараллельное движение, и поэтому ее кинетическая энергия равна

.

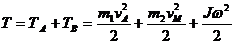Так как точка Р блока является его мгновенным центром скоро­стей, то ω = v_М/r. Кроме того, v_A = v_М = v, а момент инерции круглого однородного блока относительно центральной оси равен J = m₂r²/2, следовательно,

.

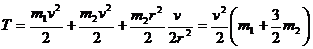Определим сумму мощностей внешних сил;

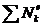= N_G + N_Q + 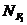+ N_F = Gv + Qv – Fv_D.

Мощность реакции 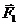равна нулю, так как эта сила приложена в мгновенном центре скоростей блока. Учитывая положение этой точки можно записать, что v_D = 2v_M = 2v. Но так как v_D = dx_D/dt, v_M = dxldt, то dx_D = 2dx, откуда, интегрируя, находим x_D = 2x. Тогда

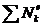= (G + Q)v - c(δ_ст+ х_D)2v = v (G + Q - 2сδ_ст - 4cх) = - 4cxv,

поскольку, как было установлено ранее, G + Q = 2сδ_ст.

Подставляя значения кинетической энергии и суммы мощно­стей в формулу теоремы, получим дифференциальное уравнение движения системы:

.

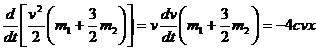Сократим на v, перенесем все члены в левую часть и разде-лим на коэффициент при ускорении dv/dt = 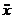груза А; это даст

.

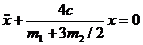Введем обозначение 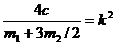(k = 7 рад/с) и получим диф­ференциальное уравнение свободных гармони-ческих колебаний c периодом Т = 2π/k = 0,9 с:

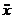+ k²x = 0,

решение которого имеет вид

х = С₁ cos kt + С₂ sin kt,

где С₁ и С₂ найдем по начальным условиям (t = 0, x₀ = 0, 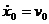), предварительно определив :

= - C₁k sin kt + C₂k cos kt.

Тогда x₀ = 0 = C₁, v₀ = C₂k, откуда C₁ = 0, С₂ = v₀/k = 2 см, и окончательно уравнение движения груза А запишется в виде

х = 2 sin 7t см..

При решении задач с помощью теоремы об измене­нии кинетической энергии в интегральной форме реко­мендуется следующая последовательность действий.

1. Изобразить систему в начальном и конечном (или заданном) положении. Построить все приложенные к системе внешние и внутренние силы (в случае неизме­няемой системы или системы, состоящей из твердых тел, соединенных идеальными связями,— только внешние си­лы, так как в этом случае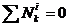

2. Записать теорему об изменении кинетической энер­гии в интегральной форме: Т₁ – Т₀ = .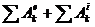

3. Подсчитать кинетическую энергию системы в на­чальном и конечном положениях, выразив ее через ско­рость звена, движение которого требуется определить (или задано).

4. Подсчитать сумму работ внешних и внутренних сил на искомых (или заданных) перемещениях точек системы, выразив их через перемещение того звена, дви­жение которого ищется (или задано).

5. Подставить полученные значения кинетической энергии и работ в формулу теоремы и найти искомую величину.

Пример 3. К барабану ворота радиусом r₁и массой т₁приложен постоянный вращающий момент М. К концу троса, на­мотанного на барабан, прикреплена ось С колеса, масса которого равна m₂. Колесо катится без скольжения вверх по наклонной плоскости, образующей угол α с горизонталью (рис. 482). Какую угловую скорость приобретет барабан, сделав п оборотов? Бара­бан и колесо считать одно­родными круглыми цилин­драми. В начальный мо­мент система находилась в покое. Массой троса и тре­нием в шарнирах пре­небречь.

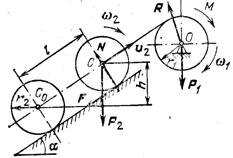Решение. Условием задачи заданы силы, дей­ствующие на систему ( 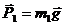, 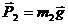), массы входящих в нее тел и ко­нечное перемещение системы (угол поворота бара­бана φ = 2πп), требуется же найти скорость в конце перемещения. Поэтому для решения задачи применим теорему об изменении кинетичес-кой энергии системы в интегральной форме:

Рис. 482 Т₁ – Т₀ = .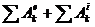

Изобразим систему в. начальном и конечном положениях вме­сте с приложенными к ней внешними силами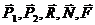и мо­ментом М. Внутренние силы не показываем, так как система со­стоит из твердых тел, соединенных идеальными связями и 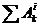= 0. В начальном положении система неподвижна, следо­вательно, Т₀ = 0. После п поворотов барабана он приобрел угло­вую скорость ω₁и скорость центра колеса будет равна v₂ = ω₁r₁, а угловая скорость колеса ω₂ = v₂/r₁ = ω₁r₁/r₂, ибо точка контакта колеса с наклонной плоскостью является его мгновенным центром скоростей. Барабан вращается вокруг неподвижной оси О, а колесо совершает плоскопараллельное движение, и поэтому кинетическая энергия системы T₁ после п оборотов барабана равна

.

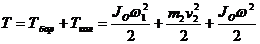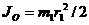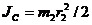По условию задачи моменты инерции барабана и колеса равны со­ответственно и ,поэтому

.

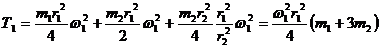При повороте барабана па угол φ = 2πn центр колеса переместится вдоль наклонной плоскости на расстояние

l = φr₁ = 2πпr₁, т, е. поднимется на высоту h = l sin α =

= 2πnr₁sin α . Определим работу внешних сил на этом конечном переме­щении:

.

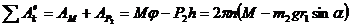Работы сил 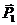и 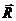равны нулю, так как они приложены в непо­движной точке О. Работы сил 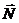и 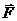равны нулю, так как они приложены в мгновенном центре скоростей колеса.

Подставим полученные значения Т и в формулу те­оремы:

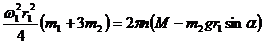
и определим ω₁: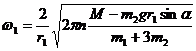

Задачи