Теорема о движении центра масс

Центр масс любой системы движется так, как двигалась бы материальная точка, имеющая массу, равную массе всей системы, если бы на нее действовала сила, равная главному вектору всех внешних сил, приложенных к данной системе.

При решении задач с использованием теоремы о движении центра масс рекомендуется следующая последовательность действий.

1. Провести оси координат, выбрав их начало в поло­жении, которое занимал центр масс системы или центр масс основной ее части в начальный момент времени или в положении статического равновесия этих точек. Оси ко­ординат направить в сторону предполагаемого движения системы. Если внешние силы, действующие на систему, параллельны, то одна из осей проводится перпендикуляр­но им.

2. Изобразить систему в смещенном в сторону поло­жительных направлений осей

3. Изобразить на рисунке приложенные к системе внешние силы. координат положении.

4. Записать формулы теоремы о движении центра масс в проекциях на выбранные оси координат:

.

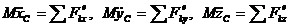5. Определить для смещенного положения системы ко­ординаты ее центра масс

,

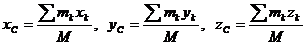и, дважды их продифференцировав, получить зависимости

.

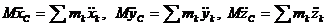6. Подставив полученные выражения в формулы тео­ремы (п. 4), определить неизвестные силы или получить дифференциальные уравнения движения интересующей нас части системы.

7. Проинтегрировать дифференциальные уравнения п. 4 или п. 6 и найти закон движения центра масс или отдель­ных ее частей.

8. Если при составлении уравнений теоремы (п. 4) , выяснится, что выполняется закон сохранения движения центра масс и, кроме того, начальная скорость центра масс по условиям задачи равна нулю, то решение сводит­ся к определению координат центра масс системы в на­чальный и текущий (или заданный) моменты времени и приравниванию полученных выражений друг другу.

Пример 1. Корпус кривошипно-ползунного механизма сво­бодно установлен на гладком основании (рис. 377). Масса корпу­са m₁, кривошипа ОА т₂, шатуна AВ т₃, ползуна В т₄ длины ОА = АВ = l. Найти переме­щение корпуса механизма в зависимости от угла поворота кривошипа, если в начальный момент система неподвижна, φ₀ = 0, а кривошип приводит­ся в движение за счет внут­ренних сил.

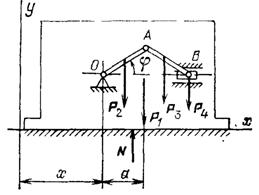Решение:Так как ос­новное тело (корпус) совер­шает поступательное движе­ние, то для решения задачи применим теорему o движе­нии центра масс. Все внешние силы - веса частей ме­ханизма и реакция плоско­сти - вертикальны, поэтому проведем ось х горизонтально и выберем начало отсчета ко­ординаты х, определяющей положение шарнира О, т. е. корпу­са механизма, в его начальном положений.

Рис. 377

Изобразим систему в положении, смещенном относительно начального. К ней приложены внешние силы: силы тяжести

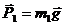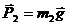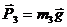, , и реакция 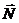. Запишем теорему в проекции на ось х:

,

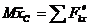так как все силы вертикальны. Следовательно, выполняется закон сохранения движения центра масс в проекциях на данную ось, и

.

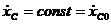По условию, в начальный момент система неподвижна, поэтому

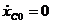и

и 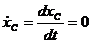в процессе движения системы положение центра масс остается неизменным:

х_С = х_С0.

Задача свелась к определению координат центра масс в на­чальном и текущем положениях системы и приравниванию их друг другу. Если φ ≠ 0, то

,

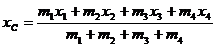где х₁ = х + а, х₂ = х + (l/2) cos φ, х₃ = х + (3l/2) cos φ,

х₄ = х + 2l cos φ,

В начальный момент φ = 0, x₀ = 0 и

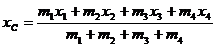
Из равенства х_С = х_С0находим

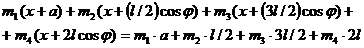
или

,

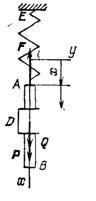
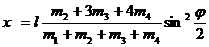т. е. при равномерном вращении кривошипа корпус будет совер­шать гармонические колебания.

Пример 2.По стержню А В массой т₁= 0,8 кг, подвешенному на пружине АЕ жесткостью с = 196 Н/м, движется ползун D массой m₂ = 0,2 кг (рис. 378); закон относительного движения ползуна s = l(1+ sin pt), где l = 4 см, р = 10 рад/с. Найти вынужденные колебания стержня.

Решение. Выберем начало координат в

Рис. 378 поло­жении, которое занимает точка А стержня в положе­нии статического равновесия. В этом положении упругая сила пружины, равная сδ_ст, уравновеши­вает силы тяжести Р = m₁g и Q = m₂g. Поместим систему в промежуточном положении, приложим к ней внешние силы и составим уравнение теоремы о движении центра масс в проекции на ось х.

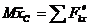= Р + Q –c (δ_ст + x)= (а)

= P + Q - cδ_ст - сх = - сх.

Определим для данного положения координату центра масс:

,

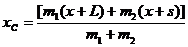откуда

.

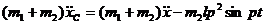Подставив выражение для 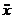в формулу (а), получим дифферен­циальное уравнение движения стержня

,

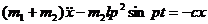или

.

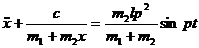Введем обозначения: 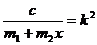, 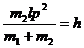. Тогда

,

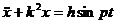где k = 14 рад/с, h = 80 см/с². Так как k ≠ р, то уравнение вынуж­денных колебаний, определяемых частным решением дифференциального уравнения, запишется в виде

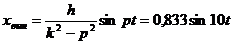см.

В рассмотренной задаче вынужденные колебания возникают за счет кинематического возбуждения.

Задачи

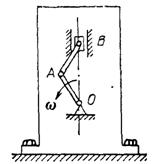3.2.1*. Корпус кривошипно-ползунного механизма укреплен на глад­ком основании с помощью болтов (рис. 379). Кривошип вращается с постоянной угловой скоростью ω. Найти силу давления корпуса на основа-ние, а также горизонтальное усилие, воспринимаемое болта-ми при работе механизма, если ОА = АВ = l = 0,5м, масса кривошипа т₁ = 1 кг, масса шатуна m₂ = 1 кг, масса ползуна т₃ = 2 кг, масса корпуса m₄ = 5 кг, ω = 14 рад/с.

Ответ: N = 88,2 - 588 cos 14t H,

Рис. 379 R = 98 sin 14t H.

3.2.2.Положение центра масс С механической системы массой т = 50 кг определяется радиус-вектором 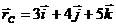. Опре­делить статический момент масс этой системы относительно плос­кости Оху. (250)

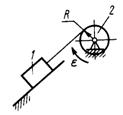
3.2.3.Определить координату х_С центра масс кривошипно-ползунного механизма (рис. 380) при уг­лах φ = 90° и α = 30°, если масса кривошипа 1 равна 4 кг, а масса шатуна 2 равна 8 кг. Ша­тун 2 длиной 0,8 м считать однородным стерж­нем. Массой ползуна 3 пренебречь.(0,231)

3.2.4. Тело массой т = 2 кг движется по гори­зонтальным направляющим (рис. 381) согласно закону s = 2t² + 1. Определить модуль главного вектора внешних сил, действующих на тело. (8)

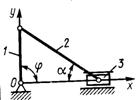
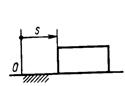
Рис. 380 Рис. 381 Рис. 382

3.2.5. Тело 1 массой т = 50 кг поднимается по наклонной плоскости с помощью троса (рис. 382), нама­тываемого на барабан 2 радиуса R = 0,4 м. Определить модуль главного вектора внешних сил, действующих на тело 1, если угловое ускорение барабана ε = 5 рад/с². (100)

3.2.6.Механическая система (рис. 383) движетсятак, что проекции ускорения ее центра масс С на оси координат равны а_Сх = 1 м/с², а_Су = 2 м/с², а_Сz = 4 м/с². Определить модуль главного вектора внешних сил, действующих на систе­му, если масса системы т = 40кг. (183)

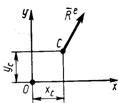
3.2.7.Движение центра масс механической систе­мы определяется радиус-вектором 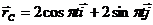(рис. 384). Определить проекцию на ось Оу главного вектора внешних сил в момент времени t = 0,5 с, если масса системы m = 10 кг. (-197)

Рис. 383 Рис. 384 Рис. 385

3.2.8.Диск массой т = 20 кг вращается равно­мерно вокруг неподвижной оси с угловой ско­ростью ω = 10 рад/с (рис. 385). Определить модуль глав­ного вектора внешних сил, приложенных к диску, если его центр тяжести удален от оси вращения на расстояние ОС = 0,5 см. (10)

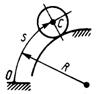
3.2.9. Центр масс колеса С (рис. 386) движется по окруж­ности радиуса R = 1,3 м согласно закону s = 4t. Определить модуль главного вектора внешних сил, приложенных к колесу, если его масса т = 15 кг. (185)

3.2.10.Кривошип 1 шарнирного параллелограмма (рис. 387) вращается равномерно с угловой скоростью ω = 5 рад/с. Определить модуль главного вектора внешних сил, действующих на звено 2, если его массат = 8кг, длина ОА = 0,4 м. (80)

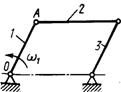
Рис. 386 Рис. 387 Рис. 388

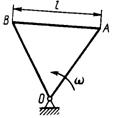
3.2.11. Однородный равносторонний треугольник ОАВ массой т = 5 кг (рис. 388) вращается равномерно вокруг неподвижной оси. Определить его угло­вую скорость ω, если главный вектор внешних сил, действующих на него, равен 300 Н, а длина l =0,4м. (16,1)

3.2.12.Шкив 2 (рис. 389)радиуса R = 0,2 м, вращаясь с угловым ускорением ε₂ = 10 рад/с², подни­мает однород-ный цилиндр 1, масса которого т = 50 кг. Определить модуль главного век­тора внешних сил, действующих на цилиндр. (50)

3.2.13. Однородный диск радиуса (рис. 390) R = 0,5 м, масса которого т = 20 кг, вращается с посто­янным угловым ускорением ε = 10 рад/с². Определить модуль главного вектора внешних сил, действующих на диск. (0)

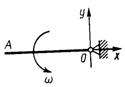
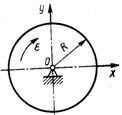
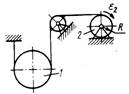
Рис. 389 Рис. 390 Рис. 391

3.2.14. Однородный стержень ОА (рис. 391) массой т = 10 кг вращается равномерно с угловой ско­ростью ω = 10 рад/с. Определить модуль глав­ного вектора внешних сил, действующих на стержень, если его длина ОА = 1 м. (500)

3.2.15.Ползун А (рис. 392) движется под действием силы 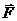с постоянной скоростью 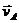. Определить реакцию направляющей на ползун А в тот мо­мент времени, когда ускорение ползуна В равно а_B = 4 м/с², если масса однородного стержня АВ равна 5 кг. Массой ползунов пре­небречь. (10)

3.2.16. Кривошип 1 (рис. 393) длинойОА = 0,25 м, враща­ясь равномерно с угловой скоростью ω = 10 рад/с, приводит в движение кулису 2, масса которой т = 5 кг. Определить модуль главного вектора внешних сил, действующих на кулису в момент времени; когда угол φ = 60°. (62,5)

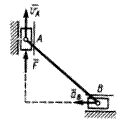
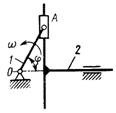
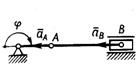
Рис. 392 Рис. 393 Рис. 394

3.2.17. Определить модуль главного вектора внешних сил, действующих на шатун АВ кривошипно-ползунного механизма (рис. 394) в момент времени, когда угол φ = 180°, а точки А и В имеют ускорения а_A = 10 м/с², a_B = 14 м/с². Шатун массой т = 5 кг считать однородным стержнем. (60)

3.2.18. Определить проекцию ускорения центра масс С механической системы (рис. 395) на ось Оу в момент времени, когда координата у_C = 0,8 м, если масса системы т = 10 кг, а главный век­тор приложенных внешних сил 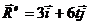. В начальный момент времени центр масс сис­темы находился в точке О в покое. (1,2)

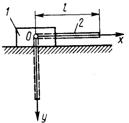
3.2.19. Тело 1 массой 4кг может двигаться по го­ризонтальной направляющей (рис. 396). На какое рассто­яние переместится тело 1, когда однородный стержень 2 массой 2 кг и длиной l = 0,6 м, опускаясь под действием силы тяжести, займет вертикальное положение. В начальный момент система находилась в покое. (0,1)

3.2.20. Тело 1 массой m = 0,7 кг (рис. 397) может дви­гаться по горизонтальной направляющей. Определить модуль ускорения тела 1 в момент времени t = 0,25 с, если относительно него под действием внутренних сил системы движется тело 2 массой т = 0,1 кг согласно 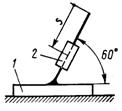уравне­нию s = sin 4t. (0,841)

Рис. 395 Рис. 396 Рис. 397

3.2.21. На тело 1 (рис. 398) действует постоянная сила F = 10 Н. Определить ускорение этого тела в момент времени t = 0,5 с, если относительно него под действием внутренних сил системы движется тело 2 согласно уравнению х = cos π t. Массы тел: m₁ = 4 кг, m₂ = 1 кг. Тела движутся поступательно. (2)

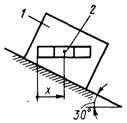
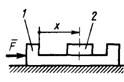
Рис. 398 Рис. 399

3.2.22. Определить ускорение тела 1 (рис. 399), скользящего по гладкой наклонной плоскости, если в гори­зонтальных направляющих относительно него под действием внутренних сил системы дви­жется тело 2 согласно уравнению х = t². Мас­сы тел: m₁ = m₂ = 1 кг. Тела движутся по­ступательно. (4,04)

3.3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ

КОЛИЧЕСТВА ДВИЖЕНИЯ

Производная по времени от количества движения системы материальных точек равна главному вектору внешних сил действующих на систему

,

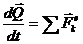или в дифференциальной форме: Дифференциал количества движения системы материальных точек равен векторной сумме элементарных импульсов действующих на систему внешних сил

.

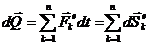Решение задач с помощью теоремы об изменении ко­личества движения по сравнению с решением задач с ис­пользованием дифференциальных уравнений движения системы упрощается, поскольку применение теоремы ис­ключает необходимость рассмотрения внутренних сил си­стемы. Решение оказывается особенно простым в том случае, когда выполняется закон сохранения количе­ства движения.

Решение задачи с помощью теоремы обизменении ко­личества движения рекомендуется проводить в следую­щей последовательности.

1. Изобразить систему в положении, которое она зани­мает в промежуточный момент времени (t > 0).

2. Изобразить на рисунке все приложенные к системе внешние силы (как активные, так и реакции связей).

3. Провести оси координат. Если на систему действу­ют только параллельные силы, то одна из осей проводит­ся перпендикулярно направлению действия сил, в противном же случае оси проводятся наиболее естественным способом, вытекающим из условия задачи. Начало коор­динат следует совместить с положением основного тела при t = 0 или с положением его статического равновесия.

4. Составить уравнения теоремы об изменении коли­чества движения в проекциях на выбранные, оси коорди­нат в дифференциальной форме:

dQ_х/dt = 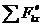, dQ_y/dt= 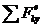, dQ_z/dt = ,

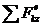или в интегральной форме:

, , .

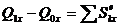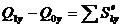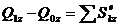4. Изобразить на рисунке абсолютные и относитель­ные скорости тел системы и подсчитать проекции коли­чества движения системы на оси координат. Необходимо иметь в виду, что в выражения

, ,

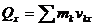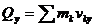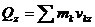
входят абсолютные скорости. Если направление скорости какой-либо точки заранее не­известно, то скорость направляют в сторону положитель­ных направлений осей координат.

6. Подставив выражения проекций количества движе­ния системы в формулы теоремы (п. 4), определить не­известные силы пли получить дифференциальные уравнения движения интересующей нас части системы.

7. Проинтегрировать полученные дифференциальные уравнения и найти искомые неизвестные.

8. Если выполняется закон сохранения количества движения или какой-либо его проекции (т. е. если 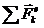= 0 или 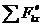= 0 и, следовательно, 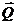= const = 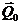или

Q_x= const = Q_x0), то задача сводится к определению количеств движения системы (или их проекции) в на­чальный и заданный (или текущий) моменты времени и приравниванию их друг другу

Пример 1. На железнодорожной платформе, свободно стоя­щей на рельсах, установлена лебедка А с барабаном радиусом r (рис. 400). Лебедка предназначена для перемещения по платформе гру­за B массой т₁. Масса платформы с лебедкой m₂. При включении ле­бедки барабан вращается по закону, ω = f(t) рад/с. В начальный момент система неподвижна. Пренебрегая трением, найти закон изменения скорости платформы после включе­ния лебедки.

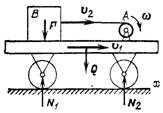Решение. Чтобы исключить неизвестные силы взаимодействия между лебедкой и платформой, лебедкой и грузом, грузом и платформой, рассмотрим платформу, лебедку и груз как единую механическую систему. Тогда все внешние силы, действующие на эту систему (силы тяжести 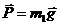, 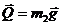и реакции 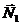, 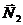) будут вертикальными. Проведем ось х перпендикулярно им и за­пишем теорему об изменении количества движения системы в про­екциях на эту ось:

.

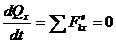Таким образом, мы имеем

Риc. 400 случай сохранения проекции

количества движения системы: Q_x= const = Q_x0, поскольку в начальный момент система неподвижна, Q_x0 = 0, и решение задачи сводится к тому, чтобы найти количество движе­нии в момент времени t > 0 и приравнять полученное выраже­ние нулю. Обозначим скорость тележки через 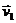и направим ее в сторону положительного направления оси х. Скорость груза В относительно платформы обозначим 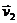; при этом v₂= ωr. Абсо­лютная скорость груза равна v_B = v₁+ v₂ = v₁ + ωr. Тогда

Q_x = m₂ v₁+ (т₁v₁ – ωr) = 0,

откуда

.

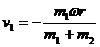Знак минус показывает, что платформа будет перемещаться в сто­рону, противоположную относительному движению груза.

Пример 2. Электрический мотор массой т₁ установлен без креплений на гладком горизонтальном фундаменте (рис. 401). На валу мотора под прямым углом за­креплен одним концом невесомый стержень длиной l, на другой конец стержня насажен точечный груз А массой m₂. В момент включения мо­тора стержень занимает вертикаль­ное положение. После включения мотора угловая скорость его вала по­стоянна и равна ω. найти:

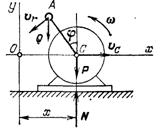1) горизонтальное движение мотора; 2) силу давления мотора на фундамент.

Решение. Изобразим мотор в положении φ = ωt > 0. К системеприложены внешние силы: силы тяжести 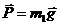, 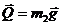и реакция фундамента 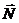. Все они

Рис. 401вертикальны, поэтому ось х проведем гори­зонтально. Начало отсчета выберем в положении, которое занимает центр мотора при φ = 0, т. е. при t = 0. Запишем теорему в про­екциях на оси координат:

dQ_х/dt= ,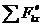

следовательно, Q_х = const = Q_х0 = 0, так как до включения мотор и груз А были неподвижны; dQ_у/dt = = 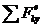= N- Р - Q, откуда N = g (m₁+ m₂)+ dQ_y/dt. Таким образом, задача сводится к определению проекций количества движения системы. Пусть центр мотора дви­жется вправо со скоростью v_c, тогда

Q_x = m₁v_c + m₂v_Ax,Q_у = m₂v_Ay,,

где 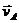— абсолютная скорость груза А. Переносной скоростью гру­за является скорость мотора 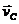, относительной — скорость при вращении груза А вокруг точки С: v_r = ωl. Тогда v_Ax= v_с – ωl cos ωt, v_Aу =-ωl sin ωt и, следовательно,

Q_x= (m₁ + m₂) v_c - m₂ωl cos ωt, Q_y = - m₂ ωl sinωt.

Так как Q_х = 0, получаем, что

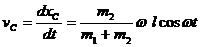
откуда 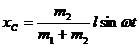+ С. Из начальных условий (t = 0, х_С = 0) находим С = 0 и окончательно

,

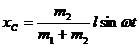т. е. центр мотора будет совершать горизонтальные гармонические колебания относительно своего начального положения с амплиту­дой m₁l/(m₁ + т₂). Сила давления мотора на фундамент по вели­чине равна реакции фундамента, действующей на мотор, поэтому

N = g (т₁+ m₂) + 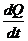= g(т₁+ т₂) - m₂ω²l cos ωt).

Минимальное значение реакции достигается при cos ωt = 1, т. е. при φ = 0, а максимальное — при φ = π:

N_min =g(m₁ — m₂) + т₂ω²l, N_max =g(m₁+ m₂) + m₂ω²l.

Если N_min < 0, то мотор начинает подпрыгивать на фундаменте. В этом случае его угловаяскорость

.

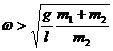Пример 3. Призма А мас­сой т₁ лежит на гладкой наклон-ной плоскости. По ней дви­жется тело В массой т₂ при­чем это относительное движе­ние происходит по закону s = nt²/2. В начальный момент тело А находится в покое. Оп­ределить зависимость скорости тела Аот времени (рис. 402).

Решение. Система состоит из двух тел: А и В. На нее действуют следующие внешние силы: 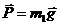- сила тяжести тела А, 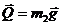- сила тяжести тела В, 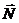- реакция наклонной плоскости. Для решения задачи применим теорему об изме­нении количества движения системы в интегральной форме в про­екциях на ось х:

,

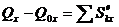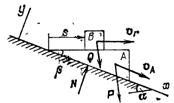где Q_0x — проекция количества движения системы в начальный момент времени, а Q_x — та же проекция в произвольный момент времени t.

Определим количество движения системы в момент t: 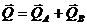, где 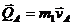-количество движения тела А, 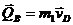—количество движения тела В, 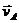и 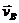— абсолютные скорости тел А и В.

Для тела В переносной

Рис.402 скоростью является скорость тела А ( 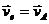), а относительная скорость 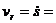nt, следовательно,

.

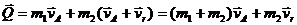Проекция количества движения системы на ось х равна

Q_x = (m₁+ m₂)v_A + m₂nt cos β.

По условию при t = 0, v_a = 0, и поэтому Q_х0 = 0. Определим про­екции импульсов внешних сил на ось х за время t:

,

,

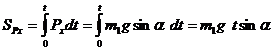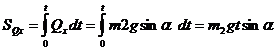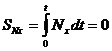, так как N_x= 0.

Подставив найденные величины в формулу теоремы, получим

(m₁ + m₂)v_А + т₂пt cos β = g(m₁+ m₂)t sin α ,

или

.

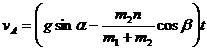Таким образом, скорость призмы А пропорциональна времени, а ее направление зависит от знака выражения, стоящего в скобках. Призма будет двигаться вверх по наклонной плоскости, если g sin α – т₂п cos β/(m₁ + m₂) < 0, т. е. если относительное ускоре­ние а_r = 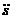= п тела В превышает значение

.

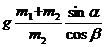Задачи