Вторая основная задача динамики материальной точки
(обратная первой)
Вторая задача динамики точки заключается в том, что задана сила, действующая на точку, и асса точки, а требуется определить закон (уравнения) движения точки.
Дано: т, F.
Определить x = f1(t); y = f2(t); z = f3(t).
Эта задача решается интегрированием дифферен-циальных уравнений движения точки:
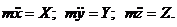
После интегрирования уравнений возникают произ-вольные постоянные. Эти произвольные постоянные определяются по начальным условиям движения. Начальные условия берутся из текста задачи. С точки зрения математики начальные условия движения точки заключаются в том, что при заданном значении аргумента (t = t0)задаются значения функций x(t0) = x0, y(t0)= y0, z(t0) = z0 и их первых производных 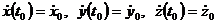 .
.
С точки зрения кинематики начальные условия движения точки заключаются в том, что при заданном значении времени (t = t0)задается положение точки
x(t0) = x0; y(t0)= y0; z(t0) = z0
и скорость точки через ее проекции на оси координат:
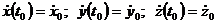 .
.
В самом общем случае правые части дифференциальных уравнений зависят от времени t, положения точки (x, у, z) и скорости 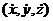 точки. Такие дифференциаль-ные уравнения интегрируются до конца только в частных случаях. Например, когда правая часть является постоянной величиной, либо простейшей функцией только времени, либо только расстояния, проходимого точкой, либо только скорости точки и др.
точки. Такие дифференциаль-ные уравнения интегрируются до конца только в частных случаях. Например, когда правая часть является постоянной величиной, либо простейшей функцией только времени, либо только расстояния, проходимого точкой, либо только скорости точки и др.
При решении второй основной задачи динамики материальной точки необходимо придерживаться следующей последовательности действий:
1) изобразить материальную точку в текущий момент времени.
2) изобразить активные силы, действующие на точку.
3) освободить точку от связей, заменяя действие связей реакциями.
4) выбирать систему координат. Начало координат системы следует помещать в начальном положении точки и оси координат направлять так, чтобы координата точки в текущий момент и проекции скорости ее на эти оси были положительными (х>0, у>0, z>0, vх >0, vy >0, vz >0).
Если точка движется по окружности, то рекомендует-ся выбирать оси естественной системы координат, сов-местив начало координат с текущим положением точки, и направить касательную к траектории точки так, чтобы для текущего положения точки естественная координата и проекция скорости точки на касательную были поло-жительными (S>0, vτ>0). Главную нормаль нужно направить в сторону вогнутости траектории.
5) cоставить дифференциальные уравнения движения точки в выбранной системе координат. При этом следует помнить, что в полученных дифференциальных уравне-ниях проекции всех сил необходимо выразить через те переменные (t, x, у, 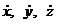 ),от которых эти силы зависят.
),от которых эти силы зависят.
6) проинтегрировать полученные дифференциальные уравнения движения точки. Способ интегрирования уравнений зависит от их вида.
Если на точку действуют, кроме постоянных сил, силы, зависящие только от одной переменной, то чаще всего такие уравнения решаются путем разделения переменных Иногда систему трех дифференциальных уравнений второго порядка:
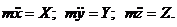
выгодно заменить эквивалентной системой, состоящей из шести уравнений, но первого порядка:
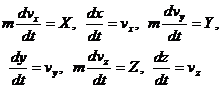 .
.
В том случае, когда по условию задачи нужно найти скорость точки как функцию текущих координат ее и сила зависит только от этих координат или скорости точки, то из дифференциальных уравнений переменную t исключаем с помощью подстановок:
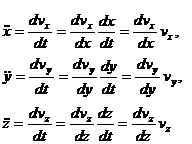 .
.
7) составить начальные условия движения по тексту задачи.
8) по начальным условиям определить произвольные постоянные интегрирования.
9) найденные произвольные постоянные подставляем в результат интегрирования дифференциальных уравне-ний движения точки. Это и будут уравнения движения точки (закондвижения).
Пример 1. Сила функция постоянная. На шероховатой наклонной плоскости (рис. 368) находится груз А веса Р1, связанный с грузом В веса Р, нитью, перекинутой через блок С. Определить закон движения грузов если вначале грузы находились в покое, коэффициент трения груза А о наклонную плоскость равен f, угол наклона плоскости к горизонту равен α
Решение. Грузы А и В можно считать материальными точками, так как эти грузы движутся поступательно. При решении задачи рассматриваем движение
каждого груза в отдельности.
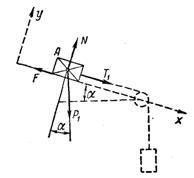
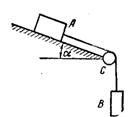
Рис. 368. Рис. 369
а) Движение груза
1. Изображаем груз А в текущий момент времени (рис. 369).
2. Изображаем активные силы: 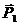 - вес груза,
- вес груза, 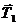 натяже-ние нити.
натяже-ние нити.
3. Освобождаем груз А от связей, заменяя действие связей реакциями. Связью является наклонная плоскость. Реакцию шероховатой опорной поверхности раскладываем на нормальную составляющую 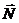 и касательную составляющую
и касательную составляющую 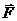 (
( 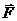 - сила трения скольжения).
- сила трения скольжения).
4. Выбираем систему координат, как указано на рис. 369.
5. Составляем дифференциальные уравнения движения точки.
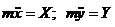
Х = ∑Хi; Х = Р1x + T1x + Fx + Nx; X = P1sin α + T1 - F;
Y = ∑Yi; Y = P1y+ T1y + Fy + Ny; Y = N – P1cos α;
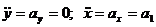 , так как направление ускорения точки А совпадает с положительным направлением оси Oх. После подстановки найденных величин в дифференциальные уравнения движения точки А, получим:
, так как направление ускорения точки А совпадает с положительным направлением оси Oх. После подстановки найденных величин в дифференциальные уравнения движения точки А, получим:
m1a1 = P1sin α + T1 - F; 0 = N – P1cos α; N = P1cos α;
F=fN; F = fP1 cos α;
m1a1 = P1(sin a - f cos a) + T1. (a)
б) Движение грузаВ:
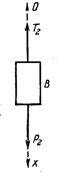 1. Изображаем груз В в текущий момент времени (рис. 370).
1. Изображаем груз В в текущий момент времени (рис. 370).
2. Изображаем активную силу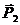 - вес грузаВ и
- вес грузаВ и 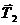
натяжение нити.
3. Выбираем систему координат, как указано на рис. 370. Достаточно выбрать одну ось Ох, так как тело движется по вертикали.
4. Составляем дифференциальное уравнение движения:
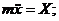 Х = ∑Хi; Х = Р2x+ Т2x = Р2 - Т2;
Х = ∑Хi; Х = Р2x+ Т2x = Р2 - Т2;
Рис. 370 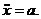 m2a2 = P2 – T2 . (б)
m2a2 = P2 – T2 . (б)
Из уравнений (а) и (б) находим ускорение грузов, имея в виду, что а1= а2 = a, Т1= Т2 = Т;
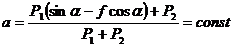 .
.
Следовательно, точки А и В движутся прямолинейно и равноускоренно:
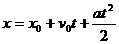 ,
,
но v0 = 0, так как грузы движутся из состояния покоя; начало координат выбираем так, что x0 = 0. Следовательно,
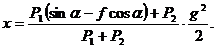
Вывод. В том случае, когда на точку, участвующую в прямолинейном движении, действуют постоянные силы, то эта точка движется равнопеременно. Ускорение равнопере-менного движения находится из дифференциальных уравнений движения. Для нахождения закона движения точки нужно найденное ускорение подставить в кинематическую формулу пути равнопеременного прямолинейного движения.
Пример 2. Сила - функция времени. Тело М начинает скользить по гладкой наклонной плоскости без начальной скорости в среде с сопротивлением, равным 0,5Ре-kt (k – неко-торое положительное число, Р - вес тела М). Определить уравнение движения тела, если угол наклона плоскости к горизонту α = 30° (рис. 371).
Решение. 1. Изображаем тело М в текущий момент времени (рис. 371); тело можно считать за точку, так как тело движется поступательно.
2. Изображаем активную силу 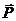 - вес тела и силу
- вес тела и силу 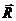 - сопротивление среды.
- сопротивление среды.
3. Освобождаем тело М от связи, заменяя действие связи нормальной реакцией 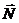 (наклонная плоскость гладкая).
(наклонная плоскость гладкая).
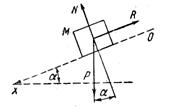
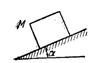
Рис. 371. Рис. 372
4. Выбираем систему координат, как указано на рис.372.
5. Составляем дифференциальное уравнение движения:
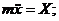 Х = ∑Хi; Х = Рx+ Rx + Nx = Р sin α - R;
Х = ∑Хi; Х = Рx+ Rx + Nx = Р sin α - R;
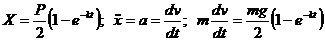 ;
;
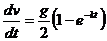 .
.
6. Интегрируем полученное дифференциальное уравнение движения точки 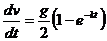 . Это уравнение с разделяющимися переменными:
. Это уравнение с разделяющимися переменными: 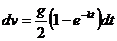 .
.
После интегрирования получим:
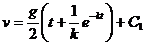 . (a)
. (a)
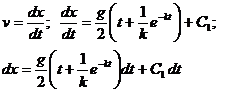 .
.
Откуда:
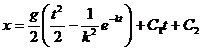 . (б)
. (б)
7. Составляем начальные условия движения (по тексту задачи) для определения произвольных постоянных интегриро-вания С1 и С2. При t = 0 х(0) = 0, 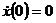 . Так как начало координат помещено в начальном положении тела М, то
. Так как начало координат помещено в начальном положении тела М, то
x(0) = 0.
8. Начальные условия движения подставляем в уравнения (а) и (б):
1) 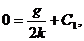 следовательно,
следовательно, 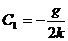 ;
;
2) 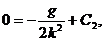 следовательно,
следовательно, 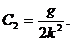
9. Найденные С1 и С2 подставляем в результат интегрирования дифференциального уравнения движения точки, уравнение (б):
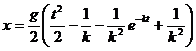 .
.
Задачи
Определение параметров прямолинейного движения по заданным силам
Тело движется вниз по гладкой плоскости, которая наклонена под углом α = 25° к горизонту. Определить ускорение тела. (4.15)
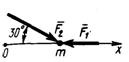 3.1.17. Материальная точка (рис. 373) массой т = 5 кг движется под действием сил F1 = 3 Н и F2 = 10 Н. Определить проекцию ускорения
3.1.17. Материальная точка (рис. 373) массой т = 5 кг движется под действием сил F1 = 3 Н и F2 = 10 Н. Определить проекцию ускорения
Рис. 373 точки на ось Ох. (1,13)
3.1.18. Тело движется вниз по наклонной шерохова-той плоскости, которая образует с горизонтом угол 40°. Определить ускорение тела, если коэффициент трения скольжения f = 0,3. (4,05)
3.1.19. Материальная точка массой m = 9 кг движется в пространстве под действием силы 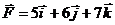 . Определить модуль ускорения точки. (1,17)
. Определить модуль ускорения точки. (1,17)
3.1.20. Моторная лодка массой т = 200 кг после остановки мотора движется прямолинейно, преодолевая сопротивление воды. Сила сопротивления R = 4v2. Определить ускорение лодки, когда ее скорость v = 5 м/с. (-0,5)
3.1.21. Тело массой т = 12 кг движется из состояния покоя по горизонтальной прямой под действием силы F = 0,6t, которая направлена по той же прямой. Определить путь, пройденный телом по истечении 10 с после начала движения. (8,33)
3.1.22. Материальная точка массой т = 0,2 кг движется вдоль осиОхпод действием силы Fx = - 0,4 t. Определить скорость точки в момент времени t = 2 с, если ее начальная скорость vx0 = 6 м/с. (2)
3.1.23. Определить путь, пройденный материальной точкой массой т пооси Ох за время t=1 с, если она движется под действием силы Fx = 12 mt2. В момент времени t0 = 0 координата x0 = 3 м, скорость v0= 6 м/с. (10)
3.1.24. Тело массой 1кг падает по вертикали, сила сопротивления воздуха R = 0,03v. Определить макси-мальную скорость падения тела. (327)
3.1.25. Материальная точка массой т = 2 кг движется по горизонтальной оси Ох под действием силы Fx = 5 cos 0,5 t. Определить скорость точки в момент времени t = 4 с, если при t0 = 0 скорость v0 = 0. (4,55)
3.1.26.Точка массой т движется по оси Ох под действием силы Fx = 6 т sin 2t. В начальный момент времени скорость точки v0x= 3 м/с. Определить в уравнении скорости постоянную интегрирования. (6)
3.1.27. Материальная точка массой т = 7 кг из состояния покоя движется по оси Ох под действием силы Fx= 7еt. Определить скорость точки в момент времени t = 2 с. (6,39)
3.1.28. На материальную точку массой т = 20 кг, которая движется по горизонтальной прямой, действует сила сопротивления R = 0,2v2. За сколько секунд скорость точки уменьшится с 10 до 5 м/с? (10)
3.1.29. На материальную точку массой т = 250кг, которая движется по горизонтальной прямой, действует сила сопротивления R = 5 v2.Определить скорость точки в момент времени t = 6 с, если t = 0 ее скорость v0 = 20 м/с. (5,88)
3.1.30. Материальная точка массой т = 4 кг движется по горизонтальной прямой. Через сколько секунд скорость точки уменьшится в 10 раз, если сила сопротивления движению R = 0,8v? (11,5)
Определение параметров криволинейного движения по заданным силам
3.1.31.Материальная точка массой т = 4 кг движется по криволинейной траектории под действием силы 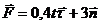 . Определить модуль ускорения точки в момент времени t = 10 с. (1,25)
. Определить модуль ускорения точки в момент времени t = 10 с. (1,25)
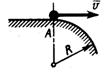 3.1.32.Материальная точка (рис. 369) массой т = 2 кг движется в плоскостиОхупод дейст-вием силы, проекции которой
3.1.32.Материальная точка (рис. 369) массой т = 2 кг движется в плоскостиОхупод дейст-вием силы, проекции которой
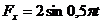 и
и 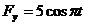 . Определить модуль ускорения точки в
. Определить модуль ускорения точки в
Рис. 374момент времени t = 1 с. (2,69)
3.1.33. Материальная точка массой т = 18 кг движется в горизонтальной плоскости по криволинейной траектории под действием силы F = 25 Н. Определить радиус кривизны траектории в момент времени, когда скорость точки v = 4 м/с, а векторы скорости и силы образуют между собой угол 55°. (14,1)
3.1.34. Тело движется по горизонтальной поверхности и в точке А отрывается от нее. Определить минимальную скорость тела в момент отрыва, если радиус R = 6 м. (7,67)
3.1.35. На горизонтальном диске на расстоянии 2 м от его вертикальной оси вращения находится тело. Опреде-лить угловую скорость равномерного вращения диска, превышение которой приведет к скольжению тела по диску, если коэффициент трения скольжения f = 0,3. (1,21)
3.1.36. Космическая станция движется по круговой орбите радиуса R = 7·106 м вокруг Земли. Определить скорость станции в км/с, если масса Земли равна 5,976·1024 кг, гравитационная постоянная равна 6,672·10-11 Н·м/кг2. (7,55)
3.1.37. Материальная точка массой т = 11 кг движет-ся по криволинейной траектории под действием равно-действующей силы F = 20 Н. Определить скорость точки в момент времени, когда радиус кривизны траектории ρ = 15 м и угол между силой и вектором скорости равен 35°. (3,96)
 3.1.38. Материальная точка массой т = 16 кг (рис.375) движется в плоскости по криволинейной траектории под действием равнодействующей силы F = 0,3t. Определить скоростьточки в момент времени t = 20 с, когда радиус кривизны траектории ρ = 12 м и угол между векторами силы и скорости α = 50°.(1,86)
3.1.38. Материальная точка массой т = 16 кг (рис.375) движется в плоскости по криволинейной траектории под действием равнодействующей силы F = 0,3t. Определить скоростьточки в момент времени t = 20 с, когда радиус кривизны траектории ρ = 12 м и угол между векторами силы и скорости α = 50°.(1,86)
3.1.39. Определить скорость точки М конического маятника, который при длине нити ОМ = 1 м описывает конус с углом при вершине α = 45°. (2,63)
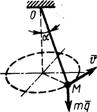
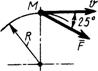 Рис. 375 3.1.40. Материальная точка М (рис. 376) массой т = 1,6 кг движется из состояния покоя в горизонтальной плоскости по окружности радиуса R = 12 м под действием силы F = 0,2t. Определить скорость точки в момент времени Рис. 376 t = 18 с, если сила образует постоянный
Рис. 375 3.1.40. Материальная точка М (рис. 376) массой т = 1,6 кг движется из состояния покоя в горизонтальной плоскости по окружности радиуса R = 12 м под действием силы F = 0,2t. Определить скорость точки в момент времени Рис. 376 t = 18 с, если сила образует постоянный
угол 25° с вектором скорости. (3,38)
