Дифференциальные уравнения высших порядков

1. Основные понятия. Дифференциальным уравнением п-го порядка назы­вается уравнение вида

F(х, у, у', у", ..., у⁽ⁿ⁾)=0.

Решением такого уравнения служит всякая п раз дифференцируемая функция у=φ(х), которая обращает данное уравнение в тождество, т. е.

F[х, φ (х), φ '(х), φ "(x),…, φ ⁽ⁿ⁾(х)]≡0.

Задача Коши для этого уравнения состоит в том, чтобы найти решение уравнения, удовлетворяющее условиям у=у₀, у'=у'₀, …, y^(n-1)=y₀ ^(n-1) при х= x₀, где x₀, y₀, у'₀, …, у^(n-1)—заданные числа, которые называются на­чальными данными, или начальными условиями.

Функция у=φ(х, С₁, С₂, ..., С_n) называется общим решением данного дифференциального уравнения п-го порядка, если при соответствующем выборе Произвольных постоянных С₁, С₂,…, С_n эта функция является решением любой задачи Коши, поставленной для данного уравнения.

Всякое решение, получаемое из общего решения при конкретных значе­ниях постоянных С₁, С₂,..., С_n, называется частным решетцем этого урав­нения. Для выделения из множества решений дифференциального уравнения определенного частного решения иногда используют и так называемые крае­вые условия. Эти условия (число которых не должно превышать порядка уравнения) задаются не в одной точке, а на концах некоторого промежутка. Очевидно, что краевые условия ставятся лишь для уравнений порядка выше первого.

Интегрирование дифференциальных уравнений n-го порядка (в конечном виде) удается произвести только в некоторых частных случаях.

2. Уравнения вида 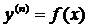. Решение этого уравнения находится n-кратным интегрированием, а именно:

………………………………………………

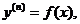
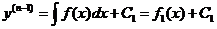
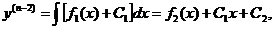
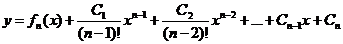
где

.

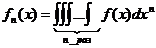Так как 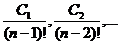являются постоянными величинами, то общее решение может быть записано и так:

.

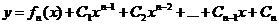643. Найти частное решение уравнения 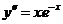, удовлетво­ряющее начальным условиям у(0)=1, y'(0)=0.

Решение. Найдем общее решение последовательным интегрированием данного уравнения:

,

,

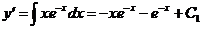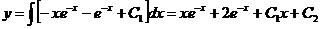или

.

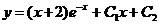Воспользуемся начальными условиями: 1=2+C₂; C₂=-1; 0=-1+C₁; С₁ = 1. Следовательно, искомое частное решение имеет вид

.

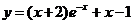Это же решение можно найти и следующим образом, используя сразу заданные начальные условия:

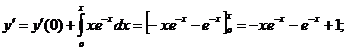
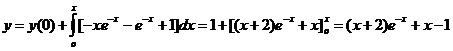
Решить уравнения:

644. .

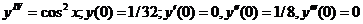645. .

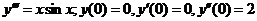646. .

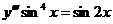647. .

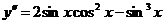648. .

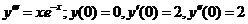3. Дифференциальные уравнения вида 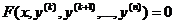, не содержащие искомой функции. Порядок такого уравнения можно понизить, взяв зановую неизвестную функцию низшуюиз производных данного урав­нения, т. е. полагая 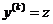. Тогда получим уравнение

.

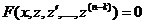Таким образом, порядок уравнения понижается на и единиц.

649. Найти общее решение уравнения ху"=у' lп(у'/х).

Решение. Полагая у'=z, преобразуем уравнение к виду

хz' =zln (z/х), или z' = (z/х)ln (z/х).

Это однородное уравнение первого порядка. Полагая z/х=1, откуда z=tх, z'=t'х+t, получим уравнение

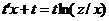, или

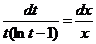
Интегрируя, находим

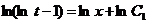или ,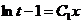

откуда 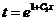; возвращаясь к переменной у, приходим к уравнению 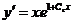. Следовательно, ^/

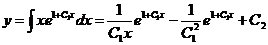
650. Тело массы т падает по вертикали с некоторой высоты без начальной скорости. При падении тело испытывает сопро­тивление воздуха, пропорциональное квадрату скорости тела. Найти закон движения тела.

Решение. Введем обозначения: пусть S—пройденный телом путь, V=ds/dt скорость, w=d²s/dt² — ускорение. На тело действуют силы: его вес Р=mg(по направлению движения) и сопротивление воздуха F=kV²=k(dS/dt)² (против на­правления движения).

На основании второго закона Ньютона приходим к следующему диффе­ренциальному уравнению движения тела;

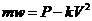, или .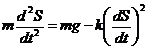

Воспользуемся начальными условиями; если t=0, то S=0, V=ds/dt=0.

Заменяя ds/dt на V, перепишем уравнение в виде

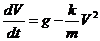
откуда, полагая mg/k=а², имеем 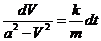. Интегрируя, находим (V≤а);

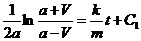
Если t=0, то V=0, откуда С₁=0. Таким образом,

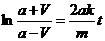
Отсюда

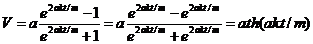
Но 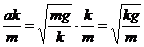; заменяя V на dS/dt , получаем для определения S уравнение

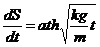
откуда, интегрируя, находим

.

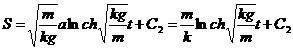Поскольку S=0 при t=0, имеем С₂=0.

Итак, закон падения тела при сопротивлении воздуха, пропорциональном квадрату скорости, описывается формулой

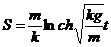
а скорость движения—формулой 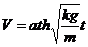Здесь 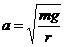. Отме­тим, что скорость падения не возрастает беспредельно, так как 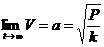( поскольку 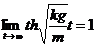), гдеР— вес тела, причем практически скорость падения достигает своего предельного значения весьма быстро, отличаясь от него на весьма малую величину. Именно такую кар­тину наблюдают на практике при затяжных прыжках с парашютом с боль­шой высоты.

Решить уравнения:

651. .

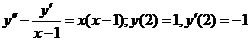652. .

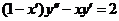653. .

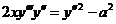654. .

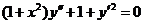655. .

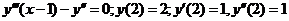4. Дифференциальные уравнения вида 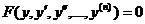, не со­держащие независимой переменной. Уравнение этого вида допускает пониже­ние порядка на единицу, если положить у' =z, а за новый аргумент принять сам у. В этом случае у", у"', ... выразятся по формулам (они выводятся по правилу дифференцирования сложной функции) 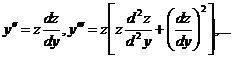через z и производные от z по у, причем порядок уравнения понизится на единицу.

656. Решить уравнение .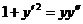

Решение. Положим у'=z, 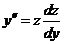. Уравнение примет вид 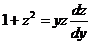, это—уравнение первого порядка относительно z с разделяющимися переменными. Разделяем переменные и интегрируем:

.

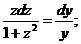
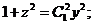
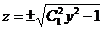Отсюда, возвращаясь к переменной у, имеем

.

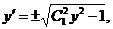
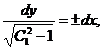
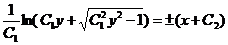или

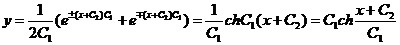
657. Найти у' из уравнения 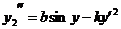при начальных условиях y(0)=0, у'(0)= 0.

Решение. Положим у’²=z; тогда 2у'у" =z' = у’ (dz/dy), т. е. 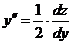. Уравнение примет вид 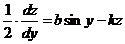. Это—линейное уравнение первого порядка относительно z:

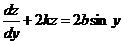
Решая его методом Бернулли, т. е. используя подстановку z=иv, получим

;

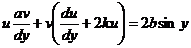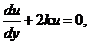
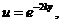
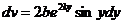
Интегрируя, находим

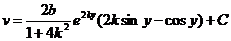
и

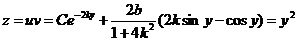
Используем начальные условия: 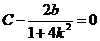, т. е. 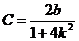откуда получаем

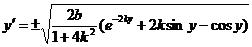
658. Найти кривую, у которой радиус кривизны равен кубу нормали; искомая кривая должна проходить через точку М (0; 1) и иметь в этой точке касательную, составляющую с осью Ох угол 45°.

Решение. Таккак радиус кривизны плоской кривой выражается формулой 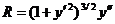, а длина нормали 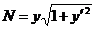, то дифференциальное уравнение задачи примет вид

.

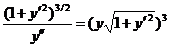Отсюда, сократив на 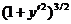, приходим к уравнению .

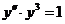Полагаяу'=z, 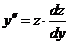, получим для z уравнение 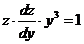. Интегрируяего, находим

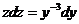, или 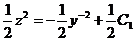, т.е.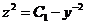

возвращаясь к переменной у, приходим к уравнению .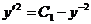

Произвольную постоянную С₁ найдем из условия, что касательная в точке М (0;1) составляет с осью Ох угол 45°, т. е. tg45°=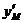= 1, или у' (0)=1. Следовательно, 1=С₁-1, т. е. С₁=2.

Таким образом, для определения у получено уравнение первого порядка

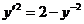, откуда 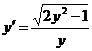; разделяем переменные и интегрируем:

.

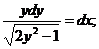
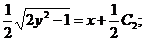
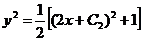Произвольную постоянную С₂ находим из условия прохождения кривой через точку M(0;1), т.е. 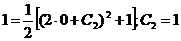. Следовательно, искомая кривая определяется уравнением

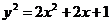
Решить уравнения:

659..

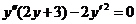660. .

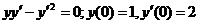661.

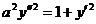
662. .

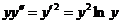663. .

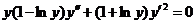664. .

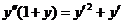665. .

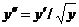5. Уравнения вида 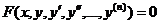однородные относительно 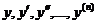. Уравнение указанного вида допускает понижение порядка на единицу при замене у'/у=z, где z—новая неизвестная функция.

666. Решить уравнение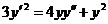

Решение. Разделим обе части уравнения на у²:

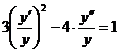
Положим 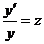, откуда 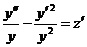, или .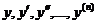

В результате получим уравнение

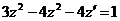, или 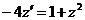,т. е.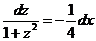

Отсюда, интегрируя, находим

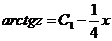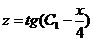, или , или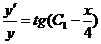

Интегрируя последнее уравнение, получим

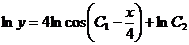или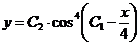

667. Решить уравнение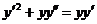

Решение. Хотя это уравнение принадлежит к предыдущему виду, егоможно проинтегрировать более простым способом. В этом уравнении левая частьесть 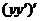, в силу чего уравнение принимает вид 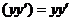или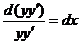

Отсюда 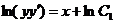, или 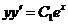, т.е. 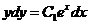. Интегрируя, находим окончательныйответ:

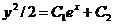
Решить уравнения:

668. 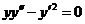. 669. .

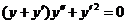670. 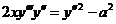671. .

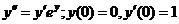672. Найти у' из уравнения 2уу"=kу—у'² при начальных условиях у (0) = 1, у' (0) = 0.

● Подстановка y‘ ^г=z.

673. Найти кривую, если проекция радиуса кривизны на ось Оу постоянна и равна а, а ось Ох касается искомой кривой в начале координат.

674. Найти кривую, у которой радиус кривизны в любой точке равен sес а, где а—угол. образованный с осью Ох каса­тельной в соответствующей точке. Искомая кривая проходит че­рез точку М (0; 1) и касательная к кривой в этой точке парал­лельна оси Ох.

675. Тело, находившееся в начальный момент в жидкости, погружается в нее под действием собственного веса без началь­ной скорости. Сопротивление жидкости прямо пропорционально скорости тела. Найти закон движения тела, если его масса m.