Простое и необычное множество. Парадоксы и Антиномии. Парадокс Рассела и его роль в математике. Способы избежать Парадокс Рассела. Логические Антиномии.

Простое и необычное множество. Парадоксы и Антиномии. Парадокс Рассела и его роль в математике. Способы избежать Парадокс Рассела. Логические Антиномии.

Относительно любого произвольно взятого множества представляется осмысленным спросить: является ли множество своим собственным элементом или нет?

Множества, не содержащие себя в качестве элемента, назовем обычными X Ï X. Например, множество всех людей не является человеком, так же как множество атомов — это не атом.

Необычными будут множества, являющиеся собственными элементами X ÎX. Например, множество, объединяющее все множества, представляет собой множество и, значит, содержит само себя в качестве элемента.

Парадокс Рассела не имеет специфически математического характера, его с легкостью можно переформулировать в чисто логических терминах.

Антиномия всемогущества. Бог всемогущ, поэтому он может создать такой камень, который сам не сможет поднять. Но Бог всемогущ, поэтому он может поднять любой камень.

Антиномия «Деревенский парикмахер» В обязанности парикмахера входит: брить всех мужчин деревни, которые не бреются сами, и только этих мужчин. Должен ли он брить самого себя?

Если да, то он будет относиться к тем, кто бреется сам, а тех, кто бреется сам, он не должен брить. Если нет, он будет принадлежать к тем, кто не бреется сам, и, значит, он должен будет брить себя.

ПАРАДОКС РАССЕЛА

Рассмотрим множество всех обычных множеств Y={X| X Ï X}. Поскольку оно множество, о нем тоже можно спрашивать, обычное оно или необычное?

Если оно обычное YÏ Y, то, согласно определению, должно содержать само себя в качестве элемента Y ÎY. Но это означает, что оно является необычным множеством.

Если оно необычное Y ÎY т.е. содержит само себя в качестве элемента, то согласно определению элементами нашего множества являются только обычные множества т.е. YÏ Y.

Итак, множество всех множеств, не являющихся собственными элементами, не содержит себя в качестве элемента тогда и только тогда когда оно содержит себя в качестве элемента. Это явное противоречие. И получено оно на основе самых правдоподобных предположений и с помощью как будто бесспорных шагов.

Полученное противоречие говорит о том, что теория, использующая в качестве неопределимых понятий – множества, способна породить новые парадоксы. Тем самым возникают сомнения в любом выводе этой теории.

После опубликования этих парадоксов сразу же стало очевидным, что ни в логике, ни в математике за всю долгую историю их существования не было выработано решительно ничего, что могло бы послужить основой для устранения антиномии. Явно оказался необходимым отход от привычных способов мышления.

Во всех рассмотренных антиномиях рассуждения опираются на допущениях, что рассматриваемые объекты существуют, несмотря на то, что при их построении было изначально заложено противоречие.

В современной математике существует три способа избежать этого парадокса.

Задать множество характеристическим свойством, которое имеет вид Y={X| XÎU, X-не содержит себя в качестве элемента }. Для Y универсальное множество не указано

Задать множество характеристическим свойством в виде процедуры, позволяющей ответить на вопрос: принадлежит элемент множеству или нет? При этом, нет процедуры позволяющей ответить на вопрос XÎХ

Теория типов. Элементарные объекты имеют тип 0. Множества имеют тип 1, множества множеств имеют тип 2. Множество ВСЕХ множеств Y не имеет типа и не определено.

Все три способа, объединяются одной идеей: на этапе построения

множества исключаются противоречивые ситуации, которые могут

привести к парадоксу.

Операции над соответствиями. Объединение, пересечение, дополнение, инволюция (обратное) соответствия, композиция соответствий.

Матрица Графически Граф

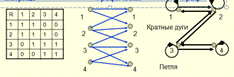
Отношение рефлексивно, если RÊD_М, где D_М – единичная матрица размера |M|×|М|

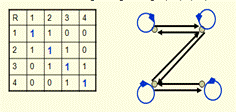
Отношение рефлексивно, если для любого элемента а∊М упорядоченная пара (а,а) ∊ R Пример: R- «жить в одном городе»

Отношение арефлексивно, если RÇDм =Æ, где D_М – единичная матрица размера |M|×|М|

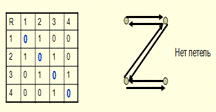
Отношение антирефлексивно, если для любого элемента а∊М упорядоченная пара (а,а) ∉ R. Пример: R- «быть начальником»

Отношение может быть не рефлексивным и не антирефлексивным

Симметричное

Если R = R^#, где R^# = {(a,b): (b,a) ÎR} обратное отношение

Для любых элементов a,b если пара (а,b)∊R, то и пара (b,a)∊R

все «1» в матрице симметричные; все дуги кратные

Антисимметричное

Если R Ç R^# Í Dм

2) Для любых элементов a и b, если (a,b) ∊ R и (b,a) ∊ R, то a=b

нет симметричных «1», на главной диагонали могут быть «1»;

нет кратных дуг, но могут быть петли

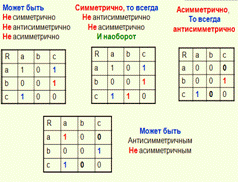
Асимметричное

Если R Ç R^# = Æ

В отношении R нет одновременно пары (a,b) и (b,a)

нет «1» на главной диагонали и симметричных;

нет ни кратных дуг ни петель

Транзитивное

Если R²ÍR

(возвести матрицу в квадрат и сравнить структуры R² и R)

Если пары (а,b) ∊ R и (b,c) ∊ R, то пара (а,с) ∊ R.

Эквивалентное отношение. Классы эквивалентности. Фактормножество по отношению эквивалентности. Толерантное отношение, отношение порядка и предпорядка. Отношение строго и нестрого порядка. Отношение полного (линейного) и неполного порядка.

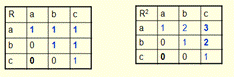
эквивалентное, если оно рефлексивно, симметрично и транзитивно

Пример: на множестве М={1,2,3,4,5,6} задано отношение

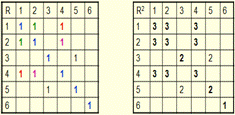
Если на множестве M задано эквивалентное отношение R, то все элементы М

можно разбить на непересекающиеся подмножества М1…Mn

(классы эквивалентности), такие что М = М1 È М2È... È Мn

М1 ∩ М2∩...∩ Мn= ø

Класс эквивалентности

Класс эквивалентности Mx, содержащий элемент х,состоит из элементов z∊M, таких что пара (z,x) ∊R.

Mx= {z∊M: (z,x) ∊R}

M1 = {z: (z,1) ∊R} = {1,2,4} M3 = {z: (z,3) ∊R} = {3,5}

M2 = {z: (z,2) ∊R} = {1,2,4} M5 = {z: (z,5) ∊R} = {3,5}

M4 = {z: (z,4) ∊R} = {1,2,4} M6 = {z: (z,6) ∊R} = {6}

M1=M2=M4 M3=M5

Множество классов эквивалентности F={M1, M2, …, Mn} называется фактор-множеством множества A по отношению R.

F={M1, M3, M6}

Число классов эквивалентности отношения эквивалентности R называют индексом множества A.

Типы Отношений

толерантное, если оно рефлексивно и симметрично;

предпорядка, если оно рефлексивно и транзитивно;

порядка, если оно транзитивно и антисимметрично;

Основные операции над нечеткими множествами: объединение, пересечение, дополнение, разность, дизъюнктивная сумма, степень множества, концентрирование и растяжение, прямое произведение нечетких множеств. Законы алгебры нечетких множеств при максимином и алгебраическом определении функции принадлежности. Законы алгебры нечетких множеств при ограниченной функции принадлежности

Таблица Кэли композиции подстановок

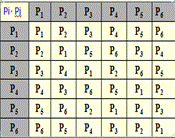
Чтобы по таблице найти обратную подстановку, надо в строчке, соответствующей рассматриваемой подстановки, найти нейтральный элемент P1; Столбец, в котором находится Р1 дает обратную подстановку. P4^-1 = P5

Группа – имеет нейтральный и обратный элемент, операция

ассоциативна Pi ∙ (Pj ∙ Pk) = (Pi ∙ Pj) ∙ Pk

Пример: Р2 ∙ (P3 ∙ P4) ? (P2 ∙ P3) ∙ P4

Р2 ∙ Р2 ? P5 ∙ P4

Р1 = Р1

Группа подстановок не абелева Pi ∙ Pj ≠ Pj ∙ Pi

Пример: P2 ∙ P3= Р5 ≠ P3 ∙ P2=Р4

Подгруппы группы подстановок

Теорема (критерий подгруппы). Непустое подмножество H группы G = <G; *> образует подгруппу, тогда и только тогда, когда:

для любых двух элементов a, b из H их композиция a * b принадлежит H;

для любого элемента a из H обратный ему элемент a^# также принадлежит H.

Группа подстановок имеет подгруппы

порядка 1: {P1}, порядка 2: {P1, P2}, {P1, P3}, {P1, P6}, порядка 3: {P1, P4, P5} и порядка 6: {P1, P2, P3, P4, P5, P6}.

Группа подстановок не абелева, но погруппы порядка 2,3 – абелевы (Pj ∙ Pj = Pj ∙ Pi). Пример: P4 ∙ P5= Р1 = P5 ∙ P4=Р1

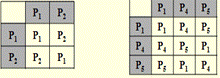
Группа симметрий фигуры.

Решетка как универсальная алгебра. Решетка как частично упорядоченное множество. Мажоранта, максимальный элемент, наименьшая верхняя (точная верхняя) грань множества Sup. Миноранта, минимальный элемент, наибольшая нижняя (точная нижняя) грань множества Inf. Связь двух определений решеток.

Решетка - алгебра с двумя бинарными операциями + , ⊗ удовлетворяющая следующим тождествам

идемпотентность,

a+ a = a, a ⊗ a = a

Коммутативность

a + b = b + a, a ⊗ b = b ⊗ a

Ассоциативность

(a + b) + c = a +(b + c), (a ⊗ b) ⊗ c = a ⊗ (b ⊗ c)

Поглощение

( a ⊗ a) + b = a, ( a + a) ⊗ b = a

Решетка — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани.

Модель M = (А; R) и В Í А

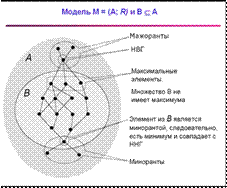
Элементаиз Аесть мажорантамножества В,если элемент

a естьпоследующий или равный элемент длявсех b из B.

Если мажоранта Î B, то она максимумоммножества B.

Если множество мажорант имеет минимум, то он единственен и его называют наименьшей верхней гранью Sup B.

Модель M = (А; R) и ВÍА

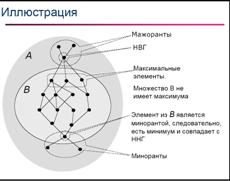
Элементаиз Аесть миноранта множества В,если элемент

a естьпредшествующий или равный элемент длявсех b из B.

Если миноранта Î B, то она минимуммножества B.

Если множество минорант имеет максимум, то он единственен и его называют наибольшей нижней гранью Inf B.

Связь двух определений решетки

Решетка - алгебра с двумя бинарными операциями "+" , "*" удовлетворяющая определенным тождествам

Решетка — частично упорядоченное множество, в котором каждое двухэлементное подмножество имеет как точную верхнюю (sup), так и точную нижнюю (inf) грани

Связь между двумя определениями решетки: a +b = sup {a, b}, a * b = inf {a, b}

Примеры решеток

Всякое линейно упорядоченное множество a £b;

sup{a, b} = b, а inf {a, b} = a

Множество всех надпространств векторного пространства, упорядоченных по включению, где inf — пересечение, а sup — объединение соответствующих надпространств

Множество всех неотрицательных целых чисел, упорядоченных по делимости: a £b , если b = ac для некоторого c. Здесь sup — наименьшее общее кратное, а inf — наибольший общий делитель данных чисел;

Типы морфизмов

Мономорфизм– это гомоморфное и инъективное соответствие

Эпиморфизм– это гомоморфное и сюръективное соответствие

Эндоморфизм – это гомоморфное соответствие и множество В=А

Биморфизм– это гомоморфное, биъективное соответствие

Изоморфизм - это гомоморфное и взаимооднозначное соответствие

Автоморфизм - это гомоморфное, взаимооднозначное соответствие и множество В=А

Изоморфизм

ИЗОМОРФИЗМ – это одно из основных понятий современной математики, которое исторически возникло сначала в пределах алгебры в применении к таким алгебраическим системам, как группы, кольца, поля и др.. Впоследствии оказалось принципиально существенным для общего понимания строения и структуры самых разных систем.

Пусть даны два множества S и S^/ , причем в первом S определены отношения F_k (x₁, x₂, ...), k = 1, 2, ..., n, а во втором S^/ –отношения F^/_k (x^/₁, x^/₂, ...), k = 1, 2, ..., n. Множества S и S^/ с указанными отношениями называются изоморфными, если между ними существует такое взаимно однозначное соответствие x^/=Г1(x), x = Г2(x^/), где xÎS, а x^/ Î S^/, что из наличия F_k (x₁, x₂, ...) вытекает наличие F^/_k (x^/₁, x^/₂, ...), и наоборот.

Отображение Г1 - изоморфное отображение или изоморфизмом системы S на систему S^/, а обратное ему отображение

Г2 – изоморфизмом системы S^/, на систему S.

Факт изоморфности систем S и S^/ обозначается S@S ^/.

47.Логическое представление исследуемой системы. Простые и сложные высказывания. Логические операции. Таблица истинности и таблица Кэли. Конверсия, инверсия, контрапозиция. Необходимое, достаточное, необходимое и достаточное условие.???

Логические представления

Логические (формальные) представления исследуемой системы — это ее описание в виде совокупности сложных высказываний, составленных из простых (элементарных) высказываний и логических связок между ними.

Логические представления характеризуются определенными свойствами и набором допустимых преобразований над ними (операций, правил вывода и т.п.), которые являются правильными методами рассуждений — законами логики.

Предмет изучения

Способы (правила) формального логического представления высказываний, построения новых высказываний из имеющихся с помощью логически выдержанных преобразований

Способы (методы) установления истинности или ложности высказываний.

Высказывание — повествовательное предложение (утверждение, суждение), о котором имеет смысл говорить, что оно истинно или ложно. Пример: «Дважды два четыре», «На улице жара».

Все научные знания, события повседневной жизни, ситуации в

экономике, управлении, политике формируются в виде

высказываний.

Простые высказывания рассматриваются в данном контексте как неделимое целое (аналогично элементу множества)

Сложные высказывания формулируются из простых с помощью логических связок (логических операций), заменяющие связки естественного языка в сложных предложениях.

Логическая операция - это функция вида f(x1,x2,…xn): Bⁿ→B, где В множество состоящее из двух элементов В={0,1}.

Логическая операция – это функция зависящая от логических переменных (т.е. принимающих значение 0,1), которая так же может принимать только два значения 0 и 1.

В таблице истинностидля бинарных операций первые два столбца содержат все возможные наборы операндов, а последующие столбцы значение логических функций.

Конъюнкция (операция логического умножения, обозначается любым из символов А&В, А ÙВ, АВ ) соответствует связывающему слову «И», «НО», «А». Значение операции А&B=1если оба операнда равны 1. Пример: «Дискретная математика легкий, но объемный предмет»

Дизъюнкция (операция логического сложения обозначается АÚВ) соответствует связывающему слову «ИЛИ». Подразумевает истинность А или В или обоих высказываний. Значение АÚВ=1 если хотя бы один из операндов равен 1. Пример: «Петров любит футбол или формулу-1»

Отрицание (операция отрицания или дополнения, обозначается любым из символовù А, Ā) соответствует связывающему слову «не верно, что» или «не …». Значение Ā=1 если А=0 и наоборот.

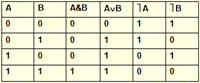
Разделительное ИЛИ (обозначается ХОR,Å₂)соответствует фразам «ИЛИ», «Либо … либо» в разделительном смысле. Значение А Å₂В =1 если значение операндов различно. Например: «Студент Иванов сдаст экзамен по дискретной математике или не сдаст».

Эквивалентность (обозначается А~В) соответствует связкам «А эквивалентно В», «А равносильно В», «А тоже, что и В», «А тогда и только тогда, когда В», «А необходимо и достаточно для В». Значение А~В=1, Если А=В. Например: «Деление числа k на 2 и 3 (А) необходимо и достаточно для деления k на 6 (В)».

«Любое число делится на 6 (А) тогда и только тогда, когда оно делится на 2 и 3 (В)».

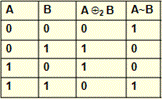
Условные высказывания типа «если А, то В», «А влечет В» соответствуют логической операции импликация. Обозначается следующим образом А®В. Пример: отец говорит сыну: «Если в этом семестре ты сдашь все экзамены на «отлично» (A), то я куплю тебе машину (B)». При каких условиях отец говорит правду?

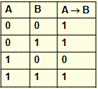
Примеры необходимых и достаточных условий

Пусть число k делится на 12 определить какие условия являются необходимыми (Н), достаточными (Д), необходимыми и достаточными (НИД)

Н Д НИД

Число делится на 2 + - -

Число делится на 3 + - -

Число делится на 4 + - -

Число делится на 6 + - -

Число делится на 24 - + -

Число делится на 36 - + -

Число делится на 2 и 3 + - -

Число делится на 3 и 4 + + +

Таблица истинности

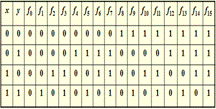
Таблица Кэли

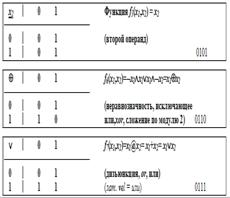
Алгебра логики. Бинарные логические операции. Существенные и несущественные (фиктивные) переменные. Функционально полные системы (базисы). Булева алгебра логики. Законы булевой алгебры. Примеры других алгебр логики.

Математическая логика состоит из двух разделов: логики высказываний и логики предикатов.

Логика высказываний может быть представлена двумя подходами: алгеброй логики (высказываний) и исчислением высказываний.

Алгебра, образованная множеством B={0,1} вместе со всеми возможными операциями на нем, называется алгеброй логики.

Алгебра логики как раздел математической логики изучает строение сложных логических высказываний (логических формул) и способы установления их истинности с помощью алгебраических методов.

Формулы алгебры логики состоят из

букв — логических (двоичных) переменных

знаков операций — логические операции (логические связки)

скобок

Каждая формула задает логическую функцию — функцию от логических переменных (т.е. принимающих значение 0,1), которая так же может принимать только два значения 0 и 1. Другими словами логическая функция имеет вид f(x1,x2,…xn): Bⁿ→B, где В множество состоящее из двух элементов В={0,1}.

Множество всех логических функций обозначается P₂, множество всех логических функций n переменных — P₂(n).

Число |P₂(n)| различных функций n переменных равно числу различных двоичных векторов длины 2ⁿ, т.е.

Суперпозиция булевых функций и ее формула. Глубина формулы. Таблицы истинности для сложных формул. Эквивалентность формул. Тождественно истинная, тождественно ложная и выполнимая функция. Единичный и нулевой набор функции.

Суперпозицией F булевых функций f₀ и f₁,...,f_mназывается функция F=f₀(g₁(x1,...,xm),...,g_n(x1,...,xm)), где каждая из функций g_i(x1, ...,xm) либо совпадает с одной из переменных (тождественная функция), либо – с одной из функций f₁,...,f_m.

Формулой называется выражение, описывающее эту суперпозицию.

Символы переменных, а также функции const_0 и const_1 считаются формулами глубины 0.

Пусть дано множество (конечное или бесконечное) исходных функцийå={f₁, ..., f_m}. Любая формула F =f₀(g₁, ..., g_n), у которой g_iÎS, n— количество аргументов f_0,, имеет глубину k=max(k₁…,k_n)+1, здесь k₁…,k_n глубины формулg₁, ..., g_n.

Формулы g₁, ..., g_n называются подформулами F. Функция f₀ называется внешней или главной операцией формулы F.

Пример: Глубина формул

Определить глубину формулы F= ((А→В)&C) ÚA.

Вначале выполняется f1= А→В. Глубина которой k1=max(0,0)+1=1

Следующей будет выполняться функция f2=f1&C. Функция f2 имеет глубину k2=max(k1,0)+1=max(1,0)+1=2

Далее выполнятся функция f3=f2ÚA, глубина которой k3=max(k2,0)+1=max(2,0)+1=3

Таким образом, глубина исходной формулы равна 3.

Таблица истинности для формулы

F= ((А→В)&C)ÚA

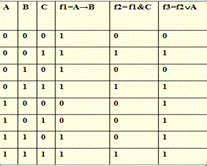
Префиксная постфиксная

Ú ( х3, х1) & x1 & ( x1 Å x2 ) ( х3 х1 Ú ) & x1 & ( x1 Å x2 )

(Úх3 х1) & x1& (Å x1x2) ( х3 х1Ú) & x1& ( x1x2 Å)

(& (Úх3 х1) x1) &(Åx1x2) (( х3 х1Ú) x1 &) & (x1 x2Å)

& &Úх3 х1 x1Åx1 x2 х3 х1Úx1 & x1x2Å&

Преобразование постфиксной формы в инфиксную

Выражение просматриваем слева направо, и его элементы помещаются в стек

Если в стеке находятся два элемента и операция (а b F), то эта тройка изымается из стека и выполняется операция

(a F b).

Результат операции помещается в стек

Просмотр строки продолжается.

Пример: представить постфиксную форму x3 x1 & x1 x1 x2Ú ÅÚ в инфиксную

x3 x1 &x1 x1 x2 Ú Å Ú

(x3& x1) x1 x1 x2 ÚÅ Ú

(x3& x1) x1 (x1Úx2)Å Ú

(x3& x1) (x1Å(x1Úx2))Ú

(x3& x1) Ú (x1Å(x1Ú x2))

Преобразование префиксной формы в инфиксную

Выражение просматриваем слева направо, и его элементы помещаются в стек

Если возникает ситуация когда в стеке находятся знак операции и две переменные (F a b), то эта тройка изымается из стека и над ними выполняется операция

(a F b).

Результат операции помещается в стек. Просмотр продолжается.

Пример: представить префиксную форму →Úх1х2&x1x3 в инфиксную

→ Ú х1 х2 & x1 x3

→ Ú х1 х2(x1&x3)

→ (х1Úх2) (x1&x3)

(х1Ú х2) → (x1&x3)

52.Элементарная конъюнкция, элементарная дизъюнкция. ДНФ, СДНФ, КНФ, СКНФ. Построение СДНФ и СКНФ по таблице истинности. Преобразования ДНФ в СДНФ. Преобразование КНФ в СКНФ.

Элементарной конъюнкциейназываются элементарные переменные либо (в разделительном смысле) их отрицания соединенные конъюнкцией ùx1 & x2 & ùx3

Элементарной дизъюнкциейназываются элементарные переменные либо (в разделительном смысле) их отрицания соединенные дизъюнкцией ùx1 Ú x2 Ú ùx3

Дизъюнктивно Нормальная Форма (ДНФ) –дизъюнкция элементарных конъюнкций (ùx1 & x2 & ùx3) Ú(x1 & ùx2 & x3)

Конъюнктивно Нормальная Форма (КНФ)–конъюнкция элементарных дизъюнкций ( ùx1 Ú x2 Ú ùx3) &( x1 Ú ùx2 Ú x3)

СДНФ и СКНФ

Совершенная Дизъюнктивно Нормальная Форма (СДНФ) –это ДНФ, у которой все элементарных конъюнкций содержат КАЖДУЮ переменную ровно один раз и все элементарные конъюнкции различны

Пример: (ùx1 & x2 &ùx3)Ú(x1 &ùx2 &ùx3)

Совершенная Конъюнктивно Нормальная Форма (СКНФ) –это КНФ у которой все элементарных дизъюнкций содержат КАЖДУЮ переменную ровно один раз и все элементарные дизъюнкции различны )

Пример: (ùx1Úx2Úùx3) & ( x1Úùx2Úx3)

Любую логическую функцию можно представить в виде СДНФ и СКНФ используя таблицу истинности.

Построение СДНФ и СКНФ

Построения СДНФ

Для каждого единичного набора переменных выписываем конъюнкцию всех переменных.

Над теми переменными, которые в этом наборе равны 0, ставим отрицание.

Все такие конъюнкции соединяем дизъюнкциями.

Построения СКНФ

Для каждого нулевого набора переменных выписываем дизъюнкцию всех переменных.

Над теми переменными, которые в этом наборе равны 1, ставим отрицание.

Все такие дизъюнкции соединяем конъюнкциями.

СДНФ – (ùx&y)Ú(x &ùy)

СКНФ – (xÚy) & (ùxÚùy)

Пример: построение полинома Жигалкина

Пусть для функции получена минимальная ДНФ:

f(x,y,z) = (ùx & y & z)Ú(x &ùz)

Используя ù a = a Å 1заменим отрицание:

f(x,y,z) = ((xÅ1) & y & z)Ú(x & (zÅ1))

Используя a Ú b = a Å b Å (a & b)заменим дизъюнкцию:

f(x,y,z) = ((xÅ1) & y & z)Å(x & (zÅ1))Å((xÅ1) & y & z & x & (zÅ1))

Используя дистрибутивность раскроем скобки:

f(x,y,z) = (x & y & z)Å(1 & y & z)Å(x & z)Å(x & 1)Å
Å(x & y & z & x & z)Å(1 & y & z & x & z)Å
Å(x & y & z & x & 1)Å(1 & y & z & x & 1)

Применим законы поглощения внутри скобок:

f(x,y,z) = (x & y & z)Å(y & z)Å(x & z)ÅxÅ(y & x & z)Å

Å(y & x & z)Å(y & z & x)Å(y & z & x)

Применим законы поглощения для одинаковых скобок

f(x,y,z) = (x & y & z)Å(y & z)Å(x & z)Åx

Классы логических функций

Класс S0: Функции «сохраняющие 0»- это логические функции, значение которых равны 0, если все аргументы равны 0: f(0,0,...,0)=0. Например Ú

Класс S1: Функции «сохраняющие 1»- это логические функции, значение которых равны 1, если все аргументы равны 1: f(1,1,...,1)=1. Например &

Класс M: "Монотонные" функции-это логические функции, которые можно выразить через & и Ú.

Монотонную функцию можно распознать по ее таблице истинности. Для этого нужно взять все пары наборов переменных, которые отличаются всего в одном столбце. Например: 0,0,0,0 и 0,0,0,1; 1,0,0,1 и 1,1,0,1. Пусть в одном наборе переменных в некотором столбце стоит "0", а в другом наборе переменных в этом же столбце стоит "1". Нельзя, чтобы значение функции при этих наборах было "1", а потом "0" соответственно. Пример монотонной функции: Ú .

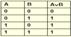
Наборы переменных Значение функций

00; 01 0; 1

00; 10 0; 1

01; 11 1; 1

10; 11 1; 1

Класс L:"Линейные" функции – этологические функции, которые можно выразить через Å, 0 и 1.

Чтобы узнать, линейна ли функция, надо выразить ее через полином Жегалкина и посмотреть, не встречается ли там операция &. Если нет, то функция линейна.

Класс D: «Двойственные» функции f и g,т.е. функции

удовлетворяющие условию f(ù x1, ù x2,..., ù xN) = ù g(x1,x2,...,xN)

Двойственные функции легко обнаружить с помощью простого приема. Надо заменить в таблице истинности все "0" на "1", а все "1" на "0". Полученная таблица истинности и будет таблицей двойственной функции. Пример & и Ú.

Класс S:"Самодвойственные" функции, т.е. функции, которые двойственны сами себе:

f(ù x1, ù x2,..., ù xN) = ù f(x1, x2,..., xN).

Критерий Поста

Система булевых функций F является полной тогда и только тогда, когда она не содержится ни в одном из классов S0, S1, S, L, M. T.е. когда в ней имеется хотя бы одна функция, не сохраняющая 0, хотя бы одна функция, не сохраняющая 1, хотя бы одна несамодвойственная функция, хотя бы одна немонотонная функция и хотя бы одна нелинейная функция.

Соотношения

pq Ú pùq = p(q Úùq)=р&1=p

Анализ коммутационных схем

Анализ коммутационных схем заключается в определении булевой формулы соответствующей рассматриваемой схемы

Для этого составляют таблицу, в которой для каждого функционального элемента определяют значения входов и выхода.

Выход последнего элемента определяет итоговую

булевую функцию.

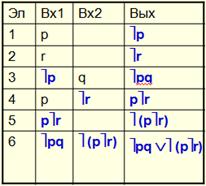
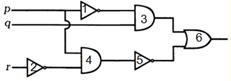
Синтез коммутационных схем

Синтез коммутационных схем заключается в построении схемы по заданной формуле

Пример: Муниципальный совет состоит из 3 человек. Каждый член совета имеет для голосования кнопку «за» и «против». Решение принимается если за него проголосует большинство. Построить коммутационную схему устройства, сигнализирующего о том, что решение принято.

Решение будет принято, если голосование пройдет по любому из вариантов pqr, ùpqr, pùqr, pqùr.Поэтому итоговая булевая функция:pqr Ú ùpqr Ú pùqr Ú pqùr

В дальнейшем, еслиэлементарная конъюнкция состоитиз n переменных,то ее функциональный элементимеет n входов.Аналогичное применяется дляэлементарной дизъюнкции.

Синтез коммутационных схем
Пример

Прежде чем строить коммутационную схему формулу следует максимально упростить, используя карту Карно или закону булевой алгебры pqr Ú ùpqr Ú pùqr Ú pqùr = pq Ú qr Ú pr = pq Ú r (qÚ p)

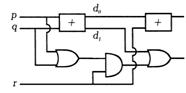
Построим схему

d0 = pùqÚùpq, d1=pq.

Проведем упрощение d0

d0 = pùqÚùpq =ùù(pùqÚùpq) =ù(ù(pùq) &ù(ùpq)) =ù((ùpÚq) & (pÚùq)) =ù(pùpÚqpÚùpùqÚqùq) =ù(qpÚùpùq ) =ù(qp) &ù(ùpùq ) = (ùpÚùq ) & (qÚp) =ù(pq ) & (qÚp)

Алгебра Россера—Тьюкетта

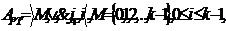конъюнкция

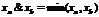характеристические функции

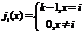Формальные теории. Принципы построения формальной теории. Задание Исчисления Высказывания как формальной теории. Выводимость формул, разрешимые и неразрешимые формулы. Свойства Исчисления Высказываний: полнота, непротиворечивость и разрешимость.

Задание Исчисления Высказываний алфавит и формулы

Алфавит исчисления высказываний состоит из переменных высказываний (пропозициональных букв): A, B, C …, знаков логических связок Ú, &, Ø, ® и скобок (, ).

Формулы:

а) переменное высказывание (пропозициональная буква) есть формула;

б) если A и B — формулы, то (A ÚB), (A &B), (A ®B) и (ØA) также формулы;

в) выражение является формулой тогда и только тогда, когда это может быть установлено с помощью пп. а) и б)

Существует несколько систем аксиом исчисления высказываний.

Выводимость формул

Если формулы F₁, …, F_n, G находятся в отношении R, то формула G называется непосредственно выводимой из F₁, …, F_n по правилу R. формулы F₁, …, F_n, называются посылками правила R, а G — его следствием или заключением.

Выводом в T формулы Gиз формул A₁, …, A_n, называется всякая последовательность F₁, F₂, ..., F_m формул такая, что F_m = G, а для любого i формула F_i есть либо аксиома теории T, либо одна из исходных формул A₁, …, A_n, либо выводима из формул F₁, …, F_i-1 по одному из правил вывода.

Если существует вывод Gиз A₁, …, A_n, то говорят, что G выводима из A₁, …, A_n т.е. является теоремой формальной теории Т. Этот факт обозначается A₁, …, A_n |— G.

Формулы A₁, …, A_n называются гипотезами или посылками вывода. Переход в выводе от F_i-1 к F_i называется i-м шагом вывода.

Непротиворечивость

Из теоремы 1 следует, что теория Тнепротиворечива.

Действительно, любая теорема в Тесть тождественно истинная

формула (тавтология). Ее отрицание не есть тавтология. Таким

образом в Тнет одновременной выводимости теоремы и ее

отрицания, что соответствует определению непротиворечивости

формальной теории.

Разрешимость

Теория Тразрешима как формальная теория.

Алгоритм, который определяет для любой формулы теории,

является ли эта формула теоремой теории, может состоять в

вычислении истинностных значений формулы в каждой

интерпретации. Принципиально это выполнимо за конечное время в

силу конечности числа интерпретаций и числа операций,

присутствующих в формуле.

58.Предикат: n-местный (n=0, n>0). Предикатные формулы. Связь между предикатами, отношениями и функциями. Модель в логике предикатов.

Предикат – повествовательное предложение, содержащее предметные переменные xi ÎMi, определенные на соответствующих множествах Mi

Например: P(x,y)=«Студент x на экзамене получил отметку y».Переменные x, yявляются предметными и принадлежат следующим множествам x={Иванов, Петров, Сидоров}, y={2,3,4,5}.

При замене переменных конкретными значениями (элементами множеств) предикат обращается в высказывание т.е. принимает значение «истинно» или «ложно». Например: «Студент Иванов на экзамене получи