Тема: Решение задач математической статистики.
Цели работы: познакомиться с основными понятиями математической статистики, научиться строить статистические ряды, полигоны и гистограммы, находить числовые характеристики выборки.
Краткое изложение темы.
Статистической совокупностью называют множество однородных предметов или явлений. Отдельные элементы, входящие в совокупность, называются членами статистической совокупности, а общее число членов совокупности — ее объемом.
Пусть у данной статистической совокупности изучается некоторый признак, который, вообще говоря, изменяется при переходе от одного члена статистической совокупности к другому. Изменение этого признака называют его вариацией, а значение признака у данного члена статистической совокупности — его вариантой.
Если произвести группировку вариант по отдельным значениям признака (дискретная группировка) или по интервалам изменения признака (интервальная группировка) и результат группировки представить рядом вариант или интервалов вариации, расположенных в порядке их возрастания, и рядом соответствующих частот, то получим вариационный ряд (соответственно дискретный или интервальный).
Под частотой значения признака или интервала понимают число членов совокупности с данной вариантой или соответственно число членов совокупности, варианты которых лежат в данном интервале.
Для наглядного представления статистического распределения пользуются графическим изображением вариационных рядов (полигоном, гистограммой).
Для построения полигона вариационного ряда на оси абсцисс прямоугольной системы координат откладывают интервалы значений признака (отдельные значения признака в случае дискретного распределения), в серединах интервалов восстанавливают перпендикуляры, длины которых пропорциональны соответствующим частотам, затем концы соседних перпендикуляров соединяют отрезками прямых, а концы крайних перпендикуляров соединяют с серединами соседних интервалов, частоты которых равны нулю. В результате получим замкнутую фигуру в виде многоугольника, называемую полигоном.
Для графического изображения интервального вариационного ряда пользуются гистограммой, построение которой осуществляется таким образом. На оси абсцисс откладывают интервалы значений признака, и на каждом из них, как на основании, строят прямоугольник с высотой, пропорциональной частоте интервала.
Мода – это наиболее часто встречающееся значение признака в данном ряду распределения. Для дискретных вариационных рядов мода определяется как значение признака с наибольшей частотой. В случае непрерывной вариации мода вычисляется по формуле
,
где 
- модальный интервал, которому соответствует наибольшая частота 
, 
- ширина интервалов вариационного ряда, 
и 
- частоты, находящиеся в соответствии с интервалами, предшествующими модальному и следующие за ним.
Медианой 
называется значение признака, относительно которого статистическая совокупность делится на две равные по объему части.
Для дискретного вариационного ряда медиана определяется непосредственно на основании определения.
Если же распределение интервальное, то сначала находят так называемый медианный интервал 
, номер которого вычисляют из неравенств 
, 
, где 
- накопленная частость в точке х.
,
где - ширина интервалов вариационного ряда,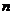 
- объем статистической совокупности, 
- накопленная частота до s-го интервала, 
- частота s-го интервала.
Примеры выполнения заданий.
Пример 1. Построить дискретный вариационный ряд и начертить полигон для следующего распределения 45 пар мужской обуви, проданных магазином за день:
Решение:
Для построения вариационного ряда различные значения признака располагаем в порядке их возрастания и под каждым из этих значений записываем его частоту.
Полигон этого распределения изображен на рисунке.
 |
Пример 2. Наблюдения за толщиной (в мм) 50 слюдяных прокладок дали следующие результаты:
| 0,021 | 0,030 | 0,039 | 0,031 | 0,042 | 0,034 | 0,036 | 0,030 | 0,028 | 0,031 |
| 0,030 | 0,033 | 0,027 | 0,031 | 0,045 | 0,028 | 0,030 | 0,033 | 0,027 | 0,031 |
| 0,036 | 0,028 | 0,024 | 0,031 | 0,040 | 0,031 | 0,033 | 0,031 | 0,034 | 0,027 |
| 0,030 | 0,048 | 0,030 | 0,046 | 0,043 | 0,030 | 0,033 | 0,028 | 0,031 | 0,051 |
| 0,034 | 0,031 | 0,036 | 0,034 | 0,037 | 0,030 | 0,039 | 0,031 | 0,042 | 0,037 |
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 0,020—0,024, второй—0,024—0,028 и т.д.) и начертить гистограмму.
Решение:
Для построения вариационного ряда составим таблицу, в первом столбце которой расположим в порядке возрастания интервалы, а во втором займемся подсчетом соответствующих частот:
Гистограмма этого распределения изображена на рисунке.
Пример 3. Найти моду и медиану распределения:
| Интервал | 120-140 | 140-160 | 160-180 | 180-200 | 200-220 | 220-240 | 240-260 | 260-280 |
| Частота |
Решение:
Так как наибольшая частота 
отвечает интервалу 180-200, то 
=180, =19, =53 и
.
Для нахождения медианы строим кумулятивный ряд:
| Интервал | 120-140 | 140-160 | 160-180 | 180-200 | 200-220 | 220-240 | 240-260 | 260-280 |
| Накопленная частота |
Номер медианного интервала s определяется из неравенств
,
или, то же самое
, 
.
В нашем случае 
, 
и 
. Поэтому медианным интервалом является 200-220, а
Ответ: 
, 
.
Задания для практической работы.
Вариант 1.
1. Построить дискретный вариационный ряд и начертить полигон распределения 60 абитуриентов по числу баллов, полученных ими на приемных экзаменах:
20 19 22 24 21 18 23 17 20 16 15 23 21 24 21 18 23 21 19 20 24 21 20 18 17 22 20 16 22 18 20 17 17 19 20 20 21 18 22 23 21 25 22 20 19 21 24 23 21 19 22 21 19 20 23 22 25 21 21 25
Вычислить основные числовые характеристики выборки.
2. Наблюдения за процентом жира в молоке 50 коров дали такие результаты:
3,86 4,06 3,67 3,97 3,76 3,61 3,96 4,04 3,84 3,94
3,98 3,57 3,87 4,07 3,99 3,69 3,76 3,71 3,94 3,82
4,16 3,76 4,00 3,46 4,08 3,88 4,01 3,93 3,71 3,81
4,02 4,17 3,72 4,09 3,78 4,02 3,73 3,52 3,89 3,92
4,18 4,26 4,03 4,14 3,72 4,33 3,82 4,03 3,62 3,91
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 3,45—3,55%, второй 3,55—3,65% и т. д.) и изобразить его графически.
Вычислить основные числовые характеристики выборки.
Вариант 2.
1. Построить дискретный вариационный ряд и начертить полигон распределения 50 пар женской обуви, проданной в магазине за один день:
37 35 36 35 38 41 40 39 35 37 39 38 41 42 40 39 38 39 40 41 42 38 39 37 39 36 38 39 40 41 38 39 36 37 39 39 38 41 43 41 42 38 39 38 38 38 37 39 39 41
Вычислить основные числовые характеристики выборки.
2. Наблюдения за процентом жира в молоке 60 коров дали такие результаты:
3,86 4,06 3,67 3,97 3,76 3,61 3,96 4,04 3,84 3,94
3,98 3,57 3,87 4,07 3,99 3,69 3,76 3,71 3,94 3,82
4,16 3,76 4,00 3,46 4,08 3,88 4,01 3,93 3,71 3,81
4,02 4,17 3,72 4,09 3,78 4,02 3,73 3,52 3,89 3,92
4,18 4,26 4,03 4,14 3,72 4,33 3,82 4,03 3,62 3,91
3,86 4,06 3,67 3,97 3,76 4,02 3,73 3,52 3,89 3,92
Построить по этим данным интервальный вариационный ряд с равными интервалами (первый интервал 3,45—3,55%, второй 3,55—3,65% и т. д.) и изобразить его графически.
Вычислить основные числовые характеристики выборки.
Приложения.
Решение квадратного уравнения:
Разложение квадратного трехчлена на множители:
1.Приравниваем к 0 -
2. Находим корни уравнения.
3. Раскладываем на множители: 
.
Формулы сокращенного умножения:
Свойства логарифмов:
1. 
, где 
и 
.
2. 
, где 
.
3. 
.
4. 
Формулы дифференцирования основных функций.
| 1) |  | 6) |  | 11) |  |
| 2) |  | 7) |  | 12) |  |
| 3) |  | 8) |  | 13) |  |
| 4) |  | 9) |  | ||
| 5) |  | 10) |  |
Основные правила дифференцирования
Пусть С – постоянная, 
, 
, имеющие производные. Тогда:
1) 
2) 
3) 
4) 
5) 
6) 
Основные формулы интегрирования:
Формула двойного угла:
Значения тригонометрических функций некоторых углов.
