Тема: Вычисление определителей. Действия над матрицами.

Практическая работа № 1.

Тема: Вычисление определителей. Действия над матрицами.

Цели работы: получить представление о матрицах, определителях 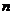-го порядка, миноре и алгебраическом дополнении и научиться выполнять различные операции над матрицами, находить обратную матрицу, вычислять определители, разлагать определители по элементам любой строки и любого столбца.

Краткое изложение темы.

Прямоугольная таблица чисел вида 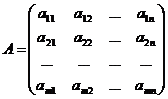называется матрицей.

Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы образуют столбцы и строки. Здесь 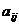— действительные числа (i = 1, 2, ..., m, j=1, 2, ..., n), i и j — соответственно индексы строки и столбца.

Произведение 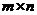числа строк на число столбцов называют размером матрицы А.

Произведением матрицы А на действительное число 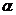называется матрица, каждый элемент которой получен умножением соответствующего элемента матрицы А на число .

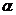Суммой матриц A и В одинакового размера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В.

Разность двух матриц одинакового размера определяется равенством: .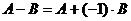

Произведением матриц 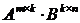называется такая матрица 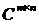, каждый элемент которой 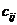равен сумме произведений элементов 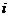-ой строки матрицы А на соответствующие элементы 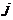-го столбца матрицы В:

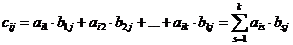, где , .

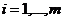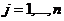Умножение матрицы А на матрицу В определено тогда и только тогда, когда число столбцов первой матрицы равно числу строк второй. В этом случае матрица А называется согласованной с матрицей В.

Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка.

Обратной для матрицы А называется такая матрица (обозначение 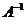), которая удовлетворяет условиям 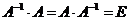, где Е – единичная матрица.

Если определитель матрицы отличен от нуля, то такая матрица называется невырожденной, если определитель матрицы равен нулю, то матрица называется вырожденной.

Теорема: Обратная матрица 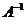существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная.

Алгоритм вычисления обратной матрицы:

1. Находим определитель исходной матрицы.

Если 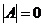, то матрица А – вырожденная и обратной матрицы 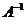не существует.

Если 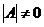, то матрица А – невырожденная и обратная матрица 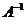существует.

2. Находим матрицу 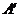, транспонированную к матрице А.

3. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу .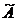

.

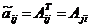4. Вычисляем обратную матрицу по формуле:

, ;

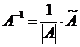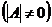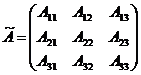
5. Проверяем правильность вычисления обратной матрицы 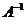, исходя из ее определения .

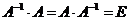Любой квадратной матрице 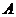порядка 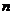можно поставить в соответствие число, называемое определителем, обозначаемое следующим образом

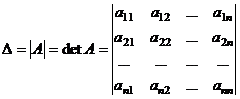
и вычисляемое по определенным правилам:

1) Квадратная матрица первого порядка есть 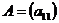, ее определитель:

.

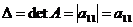2) Определитель квадратной матрицы второго порядка вычисляется по формуле:

.

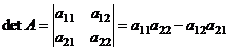3) Определитель квадратной матрицы третьего порядка вычисляется по формуле:

.

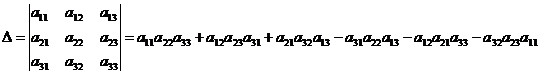4) Определитель квадратной матрицы 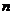-го порядка вычисляется по теореме: определитель равен сумме произведений элементов какого-нибудь столбца или строки на их алгебраическое дополнения.

Иначе говоря, имеют место следующие равенства:

· разложение определителя по элементам 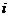-ой строки:

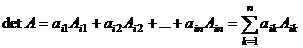
· разложение определителя по элементам 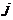-го столбца:

.

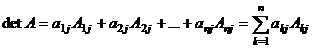Минором 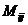элемента 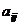определителя 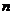-го порядка называется определитель ( 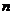-1)-го порядка, полученный из данного вычеркиванием 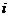-ой строки и 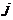-го столбца.

Алгебраическим дополнением 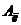некоторого элемента 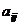называется минор этого элемента, взятый со знаком :

.

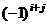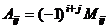Примеры выполнения заданий.

Пример 1. Даны матрицы А и В. 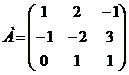, 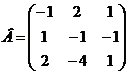Найдите: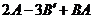

Решение:

1)

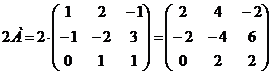
2)

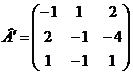
3)

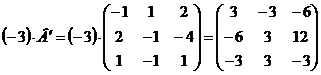
4)

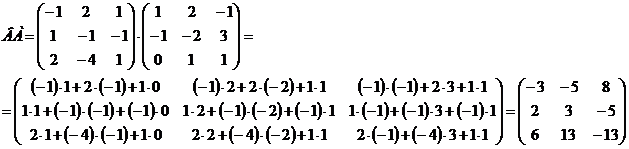
5)

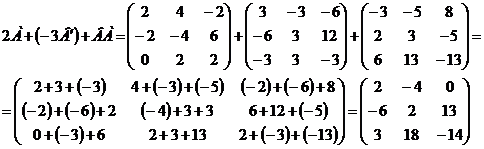
Ответ: .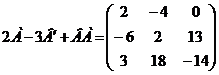

Пример 2. Вычислите обратную матрицу: .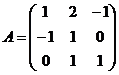

Решение:

1) Находим определитель:

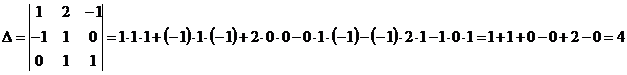
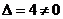, значит обратная матрица существует.

2) Находим матрицу 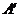, транспонированную к матрице А:

.

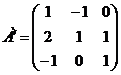3) Находим алгебраические дополнения элементов транспонированной матрицы:

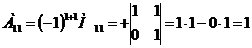
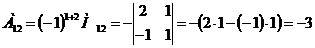
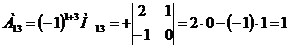
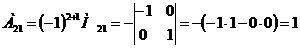
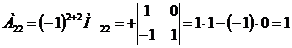
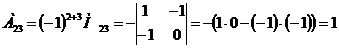
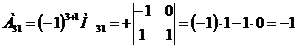
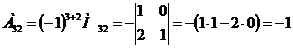
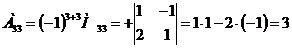
Составляем из них присоединенную матрицу :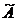

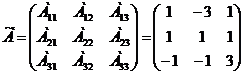
4) Находим обратную матрицу:

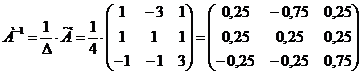
Ответ: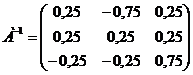

Пример 3. В определителе 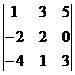алгебраическое дополнение элемента 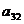равно?

Решение:

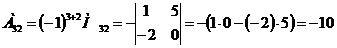
Ответ: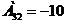

Пример 4. Решить уравнение: .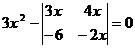

Решение:

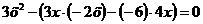
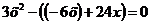
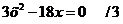
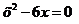
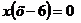
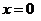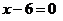
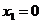или

или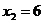

Ответ: ,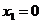

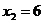
Пример 5. Вычислить определитель: .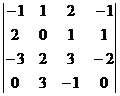

Решение:

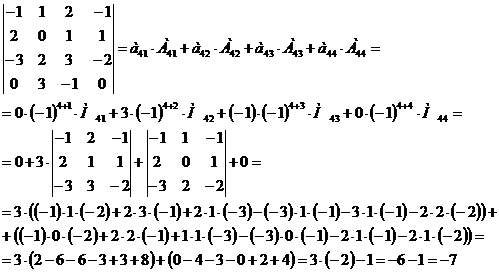
Ответ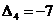

Задания для практической работы.

Вариант 1

1. Даны матрицы А и В.

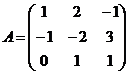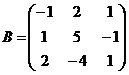, . Найдите: .

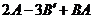2. Вычислите обратную матрицу: .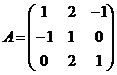

3. В определителе 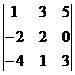алгебраическое дополнение элемента 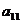равно?

4. Решить уравнение: .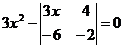

5. Вычислите определитель: .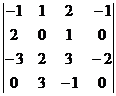

Вариант 2

1. Даны матрицы А и В.

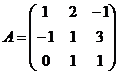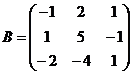, . Найдите: .

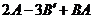2. Вычислите обратную матрицу: .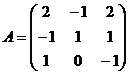

3. В определителе 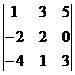алгебраическое дополнение элемента 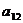равно?

4. Решить уравнение: .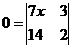

5. Вычислите определитель: .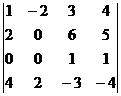

Практическая работа № 2.

Краткое изложение темы.

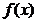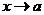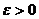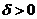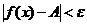Число А называется пределом функции при , если для любого сколь угодно малого найдется такое , что при 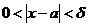. Это записывают так: .

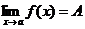Свойства пределов:

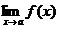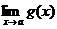Если существуют и , то

1) ,

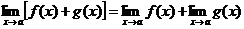2) ,

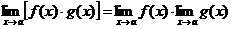3) 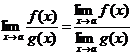(при ).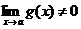

Используются также следующие пределы:

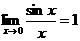(первый замечательный предел);

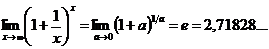(второй замечательный предел).

Правило Лопиталя раскрытия неопределенностей.

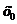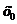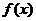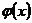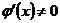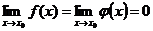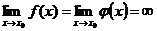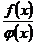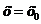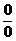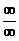Пусть в некоторой окрестности точки (кроме, быть может, самой точки ) функции и дифференцируемы и . Если или , т. е. частное в точке представляет собой неопределенность вида или , то

,

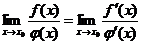если предел в правой части этого равенства существует.

Если частное 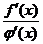в точке 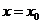также есть неопределенность вида 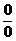или 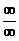и производные 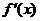и 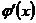удовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т. д.

В случае неопределенности вида 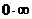или 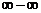следует алгебраически преобразовать данную функцию так, чтобы привести ее к неопределенности вида 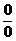или 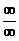и далее воспользоваться правилом Лопиталя.

Примеры выполнения заданий.

Пример 1. Найти предел .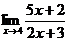

Решение:

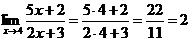
Ответ: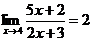

Пример 2. Найти предел .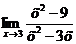

Решение:

Имеем неопределенность вида .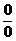

.

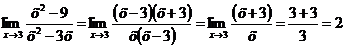Ответ: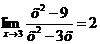

Пример 3. Найти предел .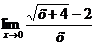

Решение:

Имеем неопределенность вида .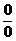

Умножим числитель и знаменатель дроби на сумму .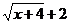

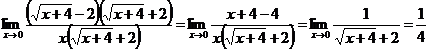
Ответ: .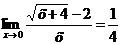

Пример 4. Найти предел .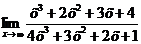

Решение:

Это – неопределенность вида 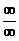. Разделим числитель и знаменатель дроби на старшую степень 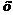, т.е. на :

.

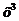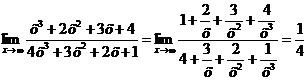Ответ: .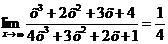

Пример 5. Найти предел .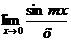

Решение:

Используя первый замечательный предел, имеем

.

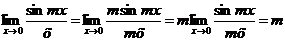Ответ: .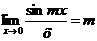

Пример 6. Найти предел .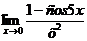

Решение:

Имеем .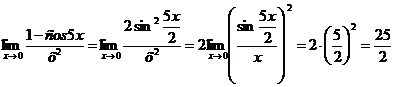

Здесь мы воспользовались результатом предыдущего примера, приняв .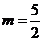

Ответ: .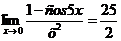

Пример 7. Найти предел .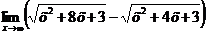

Решение:

Здесь имеет место неопределенность вида 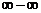. Умножим и разделим данное выражение на :

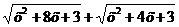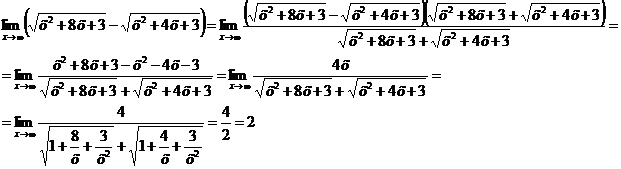
Ответ: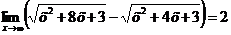

Пример 8. Найти предел .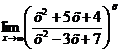

Решение:

Делением числителя на знаменатель выделим целую часть:

.

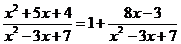Таким образом, при 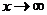данная функция представляет собой степень, основание которой стремится к единице, а показатель – к бесконечности (неопределенность вида 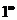). Преобразуя функцию так, чтобы использовать второй замечательный предел, получим

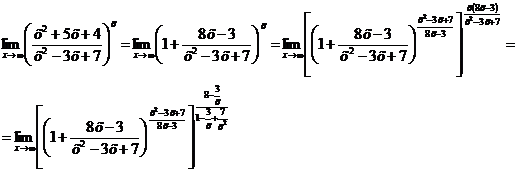
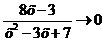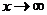Так как при , то .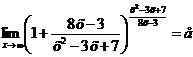

Учитывая, что 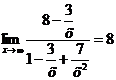, находим .

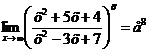Ответ: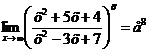

Пример 9. Найти .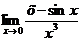

Решение:

Это – неопределенность вида 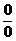. Имеем

,

так как 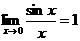. Здесь правило Лопиталя применено дважды.

Ответ: .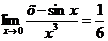

Задания для практической работы.

Вариант № 1.

Вычислите пределы:

	.
	.
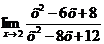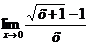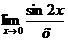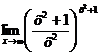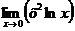Дополнительные задания:

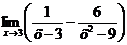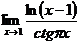Вариант № 2.

Вычислите пределы:

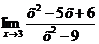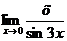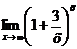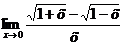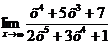Дополнительные задания:

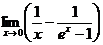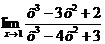Практическая работа № 3.

Краткое изложение темы.

Примеры выполнения заданий.

Задания для практической работы.

Вариант № 1.

Найти производные функций:

1. .

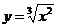2. .

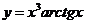3. .

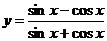4. .

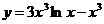5. .

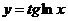6. .

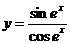7. .

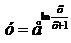Найти производную 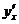от неявных функций:

8. .

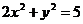9. .

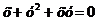10. .

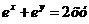Вариант № 2.

Найти производные функций:

1. .

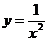2. .

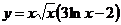3. .

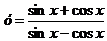4. .

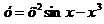5. .

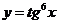6. .

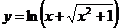7. .

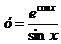Найти производную 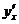от неявных функций:

8. .

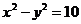9. .

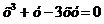10. .

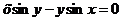Практическая работа № 4.

Краткое изложение темы.

Уравнение вида

,

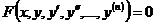связывающее аргумент 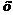, неизвестную функцию 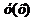и ее производные, называется дифференциальным уравнением.

Решением дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.

Дифференциальным уравнением первого порядка называется уравнение вида

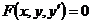
где 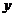— неизвестная функция; 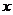— независимая переменная.

Общее решение уравнений имеет вид .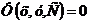

Частным решением называется решение, полученное из общего при различных числовых значениях произвольных постоянных.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

.

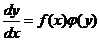Для решения этого уравнения нужно сначала разделить переменные

,

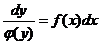а затем проинтегрировать обе части полученного равенства

.

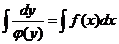Линейным дифференциальным уравнением первого порядка называется уравнение вида

,

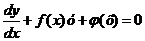где 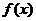и 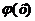- функции от х.

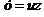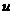Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки , где и 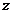- новые функции от х.

Примеры выполнения заданий.

1. Дифференциальные уравнения с разделяющимися переменными.

Пример 1. Найти общее решение уравнения .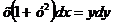

Решение:

1) Разделим переменные

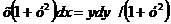, тогда

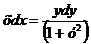
2) Интегрируем обе части полученного уравнения:

;

.

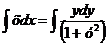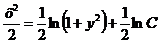Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо С написали .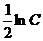

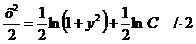
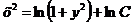
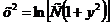
Это и есть общее решение данного уравнения.

Ответ: .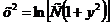

Пример 2. Найти частное решение уравнения 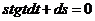, удовлетворяющее начальным условиям 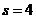при .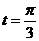

Решение:

1) Разделим переменные

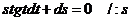
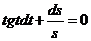
2) Интегрируем обе части полученного уравнения:

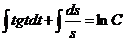
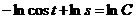
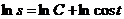
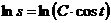
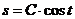- это общее решение данного уравнения.

3) Для нахождения значения произвольной постоянной С подставим значения 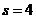и 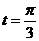в выражение для общего решения:

,

,

.

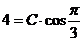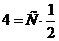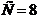Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид .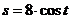

Ответ: .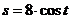

2. Линейные дифференциальные уравнения первого порядка.

Пример 3. Найти общее решение уравнения .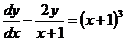

Решение:

Это линейное уравнение: здесь , .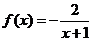

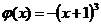Положим 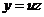и продифференцируем это равенство по х:

.

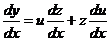Подставив теперь выражения для 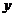и 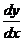в данное уравнение, получим

,

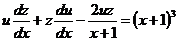или

. (*)

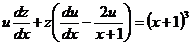Так как одну из вспомогательных функци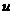й или 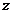можно выбрать произвольно, то в качестве 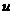возьмем одно из частных решений уравнения .

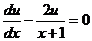Разделим в этом уравнении переменные:

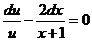
Интегрируем обе части уравнения:

,

,

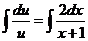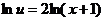(произвольную постоянную С принимаем равной 0, так как находим одно из частных решений)

,

.

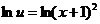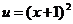Подставим теперь выражение для 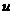в уравнение (*); тогда получим уравнение

.

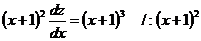
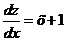Разделим переменные

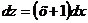
Интегрируем обе части уравнения

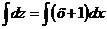
Отсюда находим

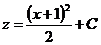
Зная 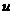и 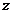, теперь получаем общее решение данного уравнения:

.

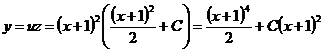Ответ: .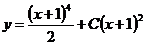

Пример 4. Найти частное решение уравнения 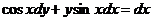, если 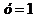при .

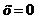Решение:

Разделив все члены данного уравнения на 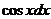, получим уравнение

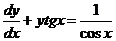, которое является линейным.

Положим 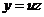; тогда .

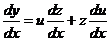Подставив теперь выражения для 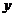и 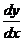в данное уравнение, получим

,

. (*)

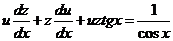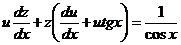Для отыскания 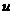получаем уравнение

,

Разделим переменные:

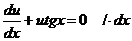
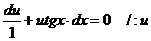
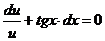
Интегрируем обе части уравнения:

,

,

.

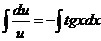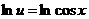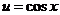Подставляя выражение для 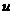в уравнение (*), имеем

,

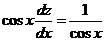Разделяем переменные

,

,

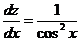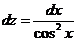Интегрируем обе части уравнения

,

.

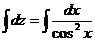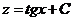Общее решение данного уравнения:

.

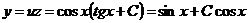Используя начальные условия 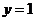, , 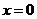имеем 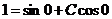, откуда .

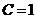Таким образом, искомое частное решение имеет вид

.

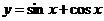Ответ: .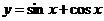

Задания для практической работы.

Вариант 1.

1. Найдите общее решение уравнения .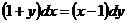

2. Найдите частное решение уравнения 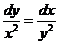, удовлетворяющего начальным условиям 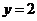при .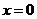

3. Найдите общее решение уравнения .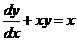

4. Найдите частное решение уравнения 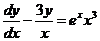, удовлетворяющего начальным условиям 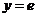при .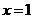

Вариант 2.

1. Найдите общее решение уравнения .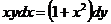

2. Найдите частное решение уравнения 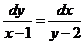, удовлетворяющего начальным условиям 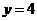при .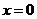

3. Найдите общее решение уравнения 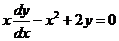. (Приведите уравнение к общему виду линейного дифференциального уравнения первого порядка).

4. Найдите частное решение уравнения 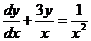, удовлетворяющего начальным условиям 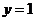при .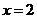

Практическая работа № 5.

Краткое изложение темы.

Уравнение, содержащее производные не выше второго порядка, называется дифференциальным уравнением второго порядка. В общем виде уравнение второго порядка записывается следующим образом:

.

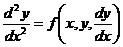Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

,

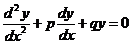где 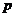и 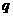- постоянные величины.

Алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:

1. Записать дифференциальное уравнение в виде .
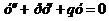2. Составить его характеристическое уравнение: 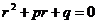(если 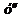обозначить через 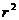, 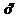- через 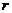, 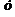- через 1).
3. Вычислить дискриминант 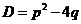; при этом если:

а) 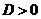, то характеристическое уравнение имеет два разных корня 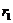и .

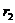Общее решение дифференциального уравнения выражается в виде

,

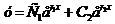где 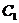и 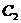- произвольные постоянные.

б) 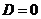, то при этом характеристическое уравнение имеет два равных корня = .

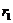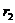Общее решение дифференциального уравнения выражается в виде

,

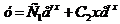где 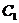и 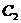- произвольные постоянные.

в) 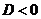, то при этом характеристическое уравнение имеет комплексные корни 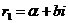и .

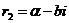Общее решение дифференциального уравнения выражается в виде

,

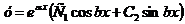где 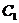и 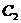- произвольные постоянные.

Примеры выполнения заданий.

Пример 1. Решить уравнение .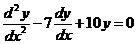

Решение:

Составим характеристическое уравнение:

.

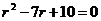Найдем корни данного уравнения:

.

,

.

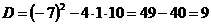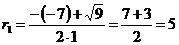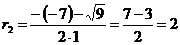Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения запишется так:

.

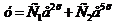Ответ: .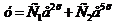

Пример 2. Решить уравнение .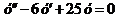

Решение:

Составим характеристическое уравнение:

.

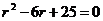Найдем его корни:

.

,

.

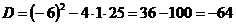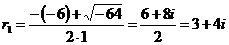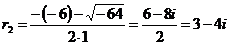Здесь , .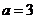

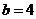Так как характеристическое уравнение имеет два комплексно-сопряженных корня, то общее решение дифференциального уравнения записывается в виде

.

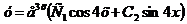Ответ: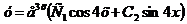

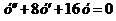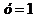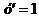Пример 3. Найти частное решение уравнения , если и при .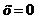

Решение:

Составим характеристическое уравнение

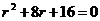
Найдем его корни

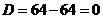
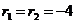
Так как корни действительные и равны, то общее решение данного дифференциального уравнения записывается в виде

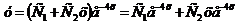
Продифференцируем общее решение

.

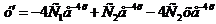Подставив начальные данные в выражения для 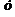и 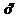, получим систему уравнений