Научиться решать задачи различными методами.

Условие задачи:

2. Найти компромиссное решение задачи, считая второй критерий наиболее предпочтительным. Его отклонение от минимального значения 20%:

f1=2*x₁+4*x₂ (max)

f2= x₁ + x₂ (min)

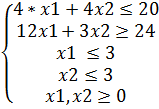
Решение:

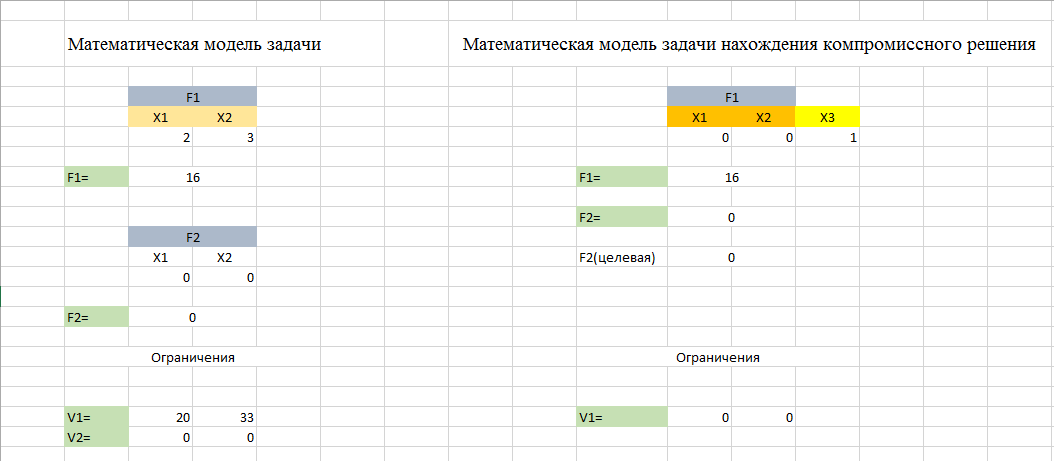
Контрольные вопросы:

1 Какие задачи решаются методами наименьших и равных отклонений, последовательных уступок, ведущего критерия, линейной комбинации критериев?

1. Задачи оптимизации на множестве целей, каждая из которых должна быть учтена при выборе оптимального решения. Примером может служить задача составления плана работы предприятия, в которой критериями служит ряд экономических показателей.

2. Задачи оптимизации на множестве объектов, качество функционирования каждого из которых оценивается самостоятельным критерием. Если качество функционирования каждого объекта оценивается несколькими критериями (векторным критерием), то такая задача называется многовекторной. Примером может служить задача распределения дефицитного ресурса между несколькими предприятиями. Для каждого предприятия критерием оптимальности является степень удовлетворения его потребности в ресурсе или другой показатель, например, величина прибыли. Для планирующего органа критерием выступает вектор локальных критериев предприятий.

3. Задачи оптимизации на множестве условий функционирования. Задан спектр условий, в которых предстоит работать объекту, и применительно к каждому условию качество функционирования оценивается некоторым частным критерием.

4. Задачи оптимизации на множестве этапов функционирования. Рассматривается функционирование объектов на некотором интервале времени, разбитом на несколько этапов. Качество управления на каждом этапе оценивается частным критерием, а на множестве этапов - общим векторным критерием.

2 Как составить модель замещающей задачи в методе наименьших и равных отклонений?

Условие равенства отклонений запишем в виде

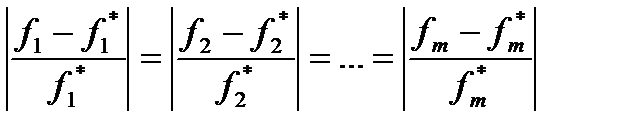
где 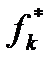— экстремальное значение целевой функции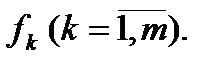

Если некоторым критериям отдается предпочтение, то в условие равенства отклонений вводятся соответствующие коэффициенты 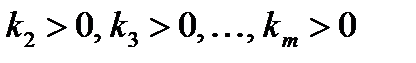(коэффициент 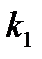считается равным единице). В этом случае соотношение примет вид:

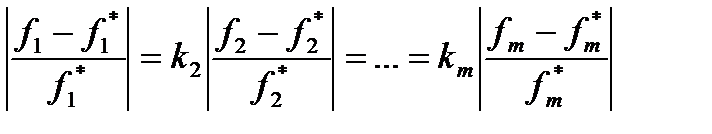
Предполагая, например, что все критерии задачи максимизируются, условие равенства отклонений после соответствующих преобразований запишем в виде

;

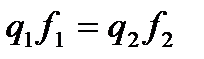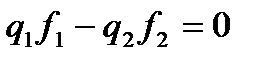
где 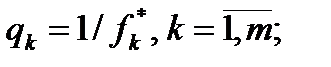m — число критериев задачи.

Для случая, когда один критерий максимизируется, а второй минимизируется, условие равенства отклонений запишется так:

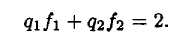
Поскольку относительные отклонения для всех критериев равны, для минимизации достаточно взять любое из отклонений. Возьмем, например, отклонение первого критерия

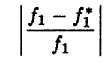
Чтобы его уменьшить, надо 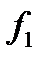увеличить, приближая 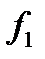к максимальному значению 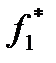. Новая задача, которая называется замещающей, решается на максимум переменной 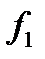. Аналогично решается замещающая задача и по второму критерию.

Для критерия, который минимизируется, например, для третьего, относительное отклонение

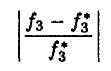
будет минимальным, когда 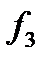окажется приближенным к своему наименьшему значению 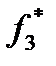, т. е. будет найден минимум функции .

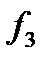В качестве целевой функции можно взять любое из следующих выражений:

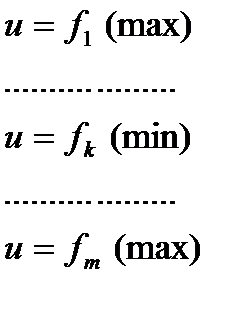
Тогда все остальные требования выполняются автоматически.

Итак, чтобы решить задачу линейного программирования методом равных и наименьших относительных отклонений, необходимо составить так называемую замещающую задачу, т. е. к системе ограничений данной задачи добавить дополнительные условия:

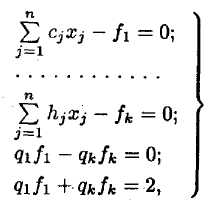
где оптимизируемые критерии 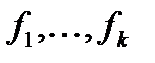включены в число неизвестных.

3 Почему дополнительное ограничение в методе наименьших и равных отклонений при стремлении обеих функций на минимум (максимум) имеет вид разности, равной нулю?

Минимум и максимум в данном случае как-бы компенсируют друг друга, т.е. как плюс и минус. Из-за этого получается ноль.

Выводы:

В ходе выполнения данной лабораторной работы мной был изучен принцип нахождения компромиссного решения задачи и составлена математическая модель её решения