Основные теоремы о конечных пределах

1. Если f (x) = const (const – константа) при ,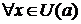
то .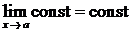

2. 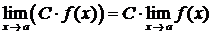, где C = const.

3. 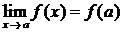, если f (x) – функция, непрерывная в точке х = а
(см. п. 6).

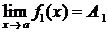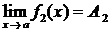4. Если и , где 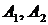– числа,
то 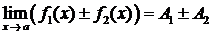, 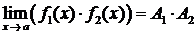и 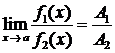при условии, что A₂ ¹ 0.

Теоремы обесконечно малых и бесконечно больших функциях(для краткости обозначим: бм – бесконечно малая функция, бб – бесконечно большая функция, огр – локально ограниченная функция).

5. бм ± бм = бм.

6. бм × бм = бм.

7. бм × огр = бм.

8. 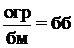, если огр не является бм.

9. бб + бб = бб, если обе бб одного знака.

10. бб × бб = бб.

11. бб × огр = бб, если огр не является бм.

12. .

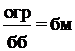Примеры.

1) 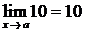(здесь использована теорема 1);

2) 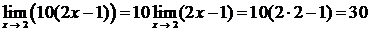(здесь использованы теоремы 2, 3 и непрерывность функции у = 2х – 1);

3) 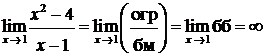(здесь использована теорема 8);

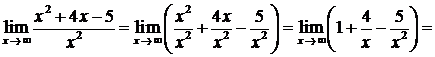
4) 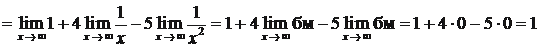(здесь использованы теоремы 2, 4 и 12).

Раскрытие неопределенностей

Если некоторый предел существует, но не может быть вычислен при помощи теорем о конечных пределах или теорем обесконечно малых, бесконечно больших и локально ограниченных функциях, то говорят, что этот предел имеет неопределенность и указывают ее вид. Основные виды неопределенностей: .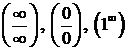

Чтобы вычислить предел, имеющий неопределенность, нужно предварительно преобразовать функцию, стоящую под знаком предела, таким образом, чтобы неопределенность исчезла, т. е. раскрыть неопределенность. Для этой цели рекомендуется использовать определенные правила.

Правило 1. Чтобы раскрыть неопределенность 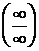при 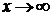, образованную отношением двух многочленов или иррациональных функций, нужно в числителе и знаменателе вынести за скобки старшие степени х
и сократить дробь на степень х.

Пример.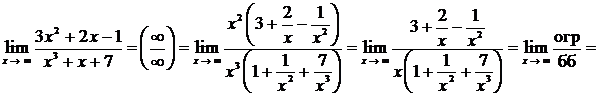

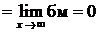(здесь использовано, что 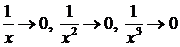при ).

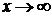Из правила 1 следует, что для раскрытия неопределенности при , образованной делением целых многочленов одинаковой степени, достаточно вычислить отношение коэффициентов при старших степенях переменной х:

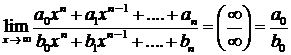. (8)

Правило 2. Чтобы раскрыть неопределенность при 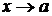, где а – число, образованную отношением двух функций, нужно в числителе
и знаменателе дроби выделить критический множитель (х – а), и сократить дробь на него.

Пример. 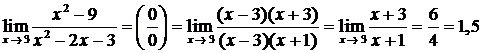(здесь критический множитель – это (х – 3), для его выделения использовано разложение многочленов на множители).

Для выделения критического множителя в случае, когда неопределен-ность образована отношением тригонометрических, показательных, или логарифмических функций, используют принцип замены бесконечно малых функций: при вычислении предела можно заменить любой бесконечно малый сомножитель на ему эквивалентный. При этом можно использовать теоретические соотношения эквивалентностей (см. формулы (1)–(7)).

Пример.

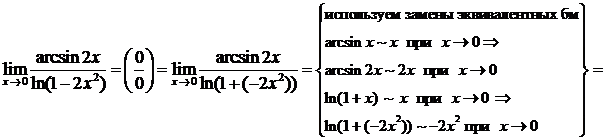
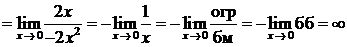(здесь критический множитель – это (х – 0) = х, для его выделения использован принцип замены эквива-лентных бесконечно малых и соотношения эквивалентностей (2) и (5)).

Правило 3. Чтобы раскрыть неопределенность (1^¥), нужно свести ее ко второму замечательному пределу, который может быть записан в двух формах:

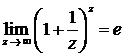или ;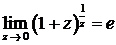

здесь е – это иррациональное число, которое можно представить в виде бесконечной непериодической десятичной дроби: е = 2,7182818… (e » 2,72).

Пример.

.

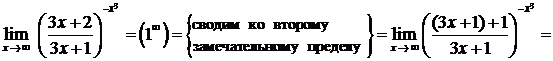
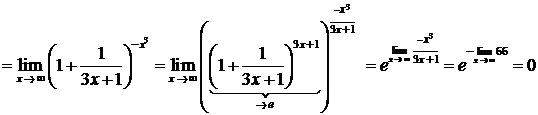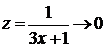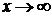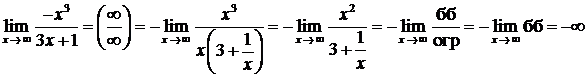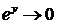При вычислении предела учтено, что при , , при 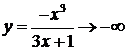.