Для экономических специальностей заочной формы обучения
Вариант 24
1. Собрание, на котором присутствуют 20 человек, в том числе 8 женщин, выбирают делегацию из 5 человек. Найти вероятность того, что в делегацию войдут 3 женщины, считая, что каждый из присутствующих может быть избран с одинаковой вероятностью.
2. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочнике соответственно равны 0,5, 0,7 и 0,9. Найти вероятность того, что хотя бы в одном справочнике этой формулы нет.
3.Имеются две урны: в первой находится 4 красных и 3 синих шара, во второй – 5 красных и 2 синих шара. Из первой урны во вторую случайным образом перекладывают два шара. После этого из второй урны берут четыре шара. Найти вероятность того, что синих и красных шаров будет одинаковое число.
4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Вероятность появления некоторого события в каждом из 5 независимых опытов равна 0,25. Определить вероятность появления этого события по крайней мере 2 раза.
б) Всхожесть семян данного сорта растений составляет 80%. Найти вероятность того, что из 700 посаженых семян число проросших будет: 1) равно 550, 2) заключено между 545 и 585.
5. Дан перечень возможных значений дискретной величины Х: x1=–1, x2=3, x3=5, а также даны математическое ожидание этой величины M[X]=0,8 и ее квадрата M[X2]=5,8. Найти закон распределения случайной величины Х.
6. Непрерывная случайная величина Х задана функцией распределения
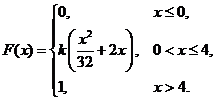
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
7. Известны математическое ожидание а=10 и среднее квадратичное отклонение s=3 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (5, 9); б) отклонения этой величины от математического ожидания не более, чем на d=7.
8. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса, используя упрощенный метод вычислений, и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 20-28 | 28-36 | 36-44 | 44-52 | 52-60 | 60-68 | 68-76 |
| n |
9. Методом наименьших квадратов подобрать функцию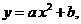 
по табличным данным и сделать чертеж.
| x | |||||||||
| y | 3,3 | 5,2 | 6,9 | 9,5 | 12,7 | 15,1 | 21,6 | ||
| Обычный курс, 5 лет | Семестр 2 | ||||||||
ВЫСШАЯ МАТЕМАТИКА
Контрольная работа №3
Для экономических специальностей заочной формы обучения
Вариант 25
1. Для уменьшения общего количества игр 10 команд случайным образом разбиты на две равные подгруппы. Определить вероятность того. Что две наиболее сильные команды окажутся в одной подгруппе.
2. Два охотника одновременно и независимо друг от друга делают два выстрела по зайцу. Какова вероятность попадания в зайца (хотя бы при одном выстреле), если вероятность попадания для первого охотника равна 0,7, а для второго – 0,8.
3.Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны 0,4, 0,3, 0,5.
4. Решить задачи, используя формулу Бернулли и теоремы Муавра-Лапласа.
а) Вероятность хотя бы одного попадания стрелком в цель при 4 выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле, если вероятность попадания в цель при одном выстреле.
б) Было посажено 500 деревьев. Вероятность того, что отдельное дерево приживется равно 0,75. Найти вероятность того, что число прижившихся деревьев: 1) равно 350, 2) больше 360, но меньше 390.
5. Дискретная случайная величина Х имеет только два возможных значения: x1 и x2, причем x1 < x2. Вероятность того, что Х примет значение x1 равно 0,3. Найти закон распределения Х, зная математическое ожидание М[X] = 1,1 и дисперсию D[X] = 1,89.
6. Непрерывная случайная величина Х задана функцией распределения
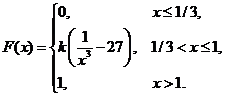
Найти: а) параметр k; б) математическое ожидание; в) дисперсию.
7. Известны математическое ожидание а=9 и среднее квадратичное отклонение s=5 нормально распределенной случайной величины Х. Найти вероятность: а) попадания этой величины в заданный интервал (4, 12); б) отклонения этой величины от математического ожидания не более, чем на d=2.
8. Из генеральной совокупности извлечена выборка, которая представлена в виде интервального вариационного ряда. а) Предполагая, что генеральная совокупность имеет нормальное распределение, построить доверительный интервал для математического ожидания с доверительной вероятностью g=0,95. б) Вычислить коэффициенты асимметрии и эксцесса, используя упрощенный метод вычислений, и сделать соответствующие предположения о виде функции распределения генеральной совокупности. в) Используя критерий Пирсона, проверить гипотезу о нормальности распределения генеральной совокупности при уровне значимости a=0,05.
| x | 7,0-7,6 | 7,6-8,2 | 8,2-8,8 | 8,8-9,4 | 9,4-10,0 | 10,0-10,6 | 10,6-11,2 |
| n |
9. Методом наименьших квадратов подобрать функцию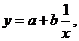 
по табличным данным и сделать чертеж.
| x | ||||||||
| y | 20,5 | 12,3 | 7,1 | 5,8 | 3,4 | 2,6 | 1,3 | 0,9 |