Проверка статистической гипотезы о законе
Проверка статистической гипотезы о законе
распределения случайной величины по 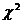 ‑ критерию Пирсона
‑ критерию Пирсона
Вариант № ___
Выполнил: студент(ка) группы ______
(ФИО) ___________________________
Проверил: к.п.н., доцент каф. «Высшая математика»
Полякова Т.А.
Дата _________2013 г. Подпись преподавателя___________
Омск, 2016
Содержание
1. Введение. Исходные данные …………………………………………………
2. Вариационный ряд ……………………………………………………………
3. Интервальный вариационный ряд ……………………………………………
4. Построение гистограммы плотностей относительных частот ……………..
5. Оценки числовых характеристик и параметров выдвинутого закона …….
6. Теоретическая функция плотности выдвинутого закона распределения ….
7. Проверка статистической гипотезы по критерию Пирсона…………............
8. Построение доверительных интервалов для М(х) и D(x). Вывод………….
(Каждый отдельный пункт содержания оформляется на отдельной странице)
Введение. Исходные данные
Математическая статистика – это раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений.
Основные задачи математической статистики математические законы теории вероятностей не являются беспредметными абстракциями, лишенными физического содержания; они представляют собой математическое выражение реальных закономерностей, фактически существующих в массовых случайных явлениях природы.
Генеральная совокупность (от лат. generis — общий, родовой) (в англ. терминологии — population) — этосовокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.
Выборочная совокупность – это часть отобранных объектов из генеральной совокупности. С понятием совокупности также связано понятие объема данной совокупности. Понятие объема совокупности относится и к выборочной, и к генеральной совокупности.
(Далее идет неупорядоченная выборка, предложенная в вашем варианте)
Вариационный ряд
Построение вариационного ряда – это первый этап статистического изучения вариации. Вариационный ряд – это упорядоченное распределение единиц совокупности чаще по возрастающим (реже убывающим) значениям признака и подсчет числа единиц с тем или иным значением признака. Когда численность единиц совокупности большая, ранжированный ряд становится громоздким, его построение занимает длительное время.
Ранжирование – это процесс выборки поисковой машиной документов из базы данных и упорядочение их по степени соответствия поисковому запросу.
(Далее идет упорядоченная выборка, представленная в виде таблицы 10 х10)
Определения и формулы для нахождения 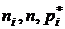 .
.
Построение гистограммы плотностей относительных частот
Гистограмма относительных частот – это фигура, состоящая из m прямоугольников, опирающихся на интервалы группировки.
Гистограмма
(По данным таблицы 1 (столбцы 2, 5) строим гистограмму)
По виду гистограммы мы подбираем соответствующий для данного случая теоретический закон распределения:
– сравниваем гистограмму с теоретическими кривыми основных законов распределения случайной величины Х (нормальный, показательный, равномерный);
– определяем параметры и числовые характеристики выбранного нами закона.
Выдвигаем гипотезу о законе распределения с.в. Х:
По виду гистограммы можно выдвинуть гипотезу о нормальном законе распределения случайной величины Х.
Закона распределения
С.в. Х распределена по нормальному (показательному, равномерному) закону, если она определена на всей числовой оси и имеет плотность. (выбираем свой вариант закона).
Плотность вероятности 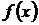 определяется по формуле (выписываем формулу плотности вероятности для своего соответствующего закона, см. Таблицу «Законы распределения с.в. Х»):
определяется по формуле (выписываем формулу плотности вероятности для своего соответствующего закона, см. Таблицу «Законы распределения с.в. Х»):
График плотности (нормального, показательного, равномерного) распределения имеет вид: (рисуем график плотности соответствующего закона распределения).
Свойства 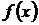 (перечисляем 4 основные свойства функции плотности):
(перечисляем 4 основные свойства функции плотности):
1. Всегда f(x)≥0, так как функция F(x) является неубывающей функцией.
2. Для функции распределения F(x) справедливо равенство:
F(x)=-∞∫xf(t)dt.
Действительно, так как по определению f(x)=F'(x), то F(x) является первообразной функцией по отношению к плотности распределения f(x). Следовательно,
-∞∫∞f(t)dt=F(t)-∞ιx=F(x)-F(-∞)=F(x)-0=F(x.)
3. Вероятность попадания случайной величины в заданный интервал [Α ; Β] равна:
P{Α≤X<Β}=Α∫βf(t)dt.
Действительно, в соответствии с формулой Ньютона-Лейбница этот определенный интеграл равен F(Β)-F(Α). По 3-му свойству функции распределения вероятностей эта разность и представляет собой вероятность P{Α≤X<Β} .
4. Интеграл от плотности распределения вероятности по всей области задания случайной величины равен единице:
-∞∫∞f(t)dt=1
Найдем теоретическую функцию 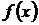 .
.
Таблица 2 (случай нормального закона).
| i | 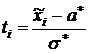 | 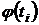 | 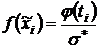 | 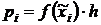 |
| - 0,63 | 0,6729 | 0,2874 | 0,169 | |
| 0,091 | 0,3973 | 0,3555 | 0,209 | |
| 0,813 | 0,2874 | 0,3752 | 0,22 | |
| 1,475 | 0,1354 | 0,3939 | 0,231 | |
| 2,137 | 0,0404 | 0,3984 | 0,234 | |
| 2,859 | 0,0067 | 0,3989 | 0,234 | |
| 3,581 | 0,0007 | 0,3989 | 0,234 | |
| 4,303 | 0,0001 | 0,3989 | 0,234 |
Таблица 2 (случай показательного закона).
| i | 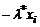 | 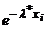 | 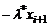 | 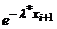 | 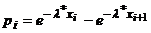 |
| - 0,949 | 0,387 | - 0,979 | 0,376 | 0,011 | |
| - 0,979 | 0,376 | - 1,01 | 0,364 | 0,012 | |
| - 1,01 | 0,364 | - 1,04 | 0,353 | 0,011 | |
| - 1,04 | 0,353 | - 1,066 | 0,344 | 0,009 | |
| - 1,066 | 0,344 | - 1,096 | 0,334 | 0,01 | |
| - 1,096 | 0,334 | - 1,127 | 0,324 | 0,01 | |
| - 1,127 | 0,324 | - 1,158 | 0,314 | 0,01 | |
| - 1,158 | 0,314 | - 1,188 | 0,305 | 0,009 |
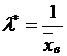
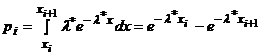
Таблица 2 (случай равномерного закона).
| i | 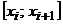 | 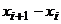 | 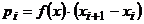 |
| 18,6; 19,2 | 0,6 | 0,208 | |
| 19,2; 19,8 | 0,6 | 0,208 | |
| 19,8; 20,4 | 0,6 | 0,208 | |
| 20,4; 20,9 | 0,5 | 0,173 | |
| 20,9; 21,5 | 0,6 | 0,208 | |
| 21,5; 22,1 | 0,6 | 0,208 | |
| 22,1; 22,7 | 0,6 | 0,208 | |
| 22,7; 23,3 | 0,6 | 0,208 |
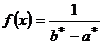 =1 / (20,863 – 17,985) = 0,347,где
=1 / (20,863 – 17,985) = 0,347,где 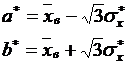 .
.
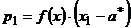 ;
;
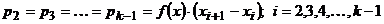 ;
;
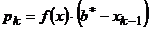 .
.
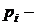 теоретические вероятности.
теоретические вероятности.
Результаты расчетов в таблицах 1-2 дают возможность построить на гистограмме выравнивающую кривую функции плотности.
(Далее строим выравнивающую кривую функции плотности (по точкам: 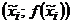 .
.
Проверка статистической гипотезы о законе
распределения случайной величины по 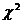 ‑ критерию Пирсона
‑ критерию Пирсона
Вариант № ___
Выполнил: студент(ка) группы ______
(ФИО) ___________________________
Проверил: к.п.н., доцент каф. «Высшая математика»
Полякова Т.А.
Дата _________2013 г. Подпись преподавателя___________
Омск, 2016
Содержание
1. Введение. Исходные данные …………………………………………………
2. Вариационный ряд ……………………………………………………………
3. Интервальный вариационный ряд ……………………………………………
4. Построение гистограммы плотностей относительных частот ……………..
5. Оценки числовых характеристик и параметров выдвинутого закона …….
6. Теоретическая функция плотности выдвинутого закона распределения ….
7. Проверка статистической гипотезы по критерию Пирсона…………............
8. Построение доверительных интервалов для М(х) и D(x). Вывод………….
(Каждый отдельный пункт содержания оформляется на отдельной странице)
Введение. Исходные данные
Математическая статистика – это раздел математики, разрабатывающий методы регистрации, описания и анализа данных наблюдений и экспериментов с целью построения вероятностных моделей массовых случайных явлений.
Основные задачи математической статистики математические законы теории вероятностей не являются беспредметными абстракциями, лишенными физического содержания; они представляют собой математическое выражение реальных закономерностей, фактически существующих в массовых случайных явлениях природы.
Генеральная совокупность (от лат. generis — общий, родовой) (в англ. терминологии — population) — этосовокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы.
Выборочная совокупность – это часть отобранных объектов из генеральной совокупности. С понятием совокупности также связано понятие объема данной совокупности. Понятие объема совокупности относится и к выборочной, и к генеральной совокупности.
(Далее идет неупорядоченная выборка, предложенная в вашем варианте)
Вариационный ряд
Построение вариационного ряда – это первый этап статистического изучения вариации. Вариационный ряд – это упорядоченное распределение единиц совокупности чаще по возрастающим (реже убывающим) значениям признака и подсчет числа единиц с тем или иным значением признака. Когда численность единиц совокупности большая, ранжированный ряд становится громоздким, его построение занимает длительное время.
Ранжирование – это процесс выборки поисковой машиной документов из базы данных и упорядочение их по степени соответствия поисковому запросу.
(Далее идет упорядоченная выборка, представленная в виде таблицы 10 х10)
Определения и формулы для нахождения 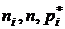 .
.
