Экстремальные задачи на графах

Независимые множества, клики, вершинные покрытия

Независимым множеством вершин графа называется любое множество попарно не смежных вершин, т.е. множество вершин, порождающее пустой подграф. Независимое множество называется максимальным, если оно не является собственным подмножеством другого независимого множества,и наибольшим, если содержит наибольшее количество вершин. Число вершин в наибольшем независимом множестве графа G обозначается через 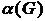и называется числом независимости графа. Задача о независимом множестве состоит в нахождении наибольшего независимого множества .

Кликой графа называется множество вершин, порождающее полный подграф, т.е. множество вершин, каждые две из которых смежны. Число вершин в клике наибольшего размера называется кликовым числом графа и обозначается через 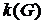. Очевидно, задача о независимом множестве трансформируется в задачу о клике и наоборот простым переходом от данного графа G к дополнительному графу , так что .

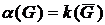Вершинное покрытие графа – это такое множество вершин, что каждое ребро графа инцидентно хотя бы одной из этих вершин. Наименьшее число вершин в вершинном покрытии графа G обозначается через 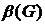и называется числом вершинного покрытия графа. В графе на рисунке 18 наибольшим независимым множеством является множество {1,2,5,7}, наибольшей кликой – множество {3,4,5,6}, наименьшим вершинным покрытием – множество {3,4,6}.

Рис. 18

Между задачами о независимом множестве и о вершинном покрытии тоже имеется простая связь благодаря следующему легко устанавливаемому факту.

Теорема 10. Подмножество U множества вершин графа G является вершинным покрытием тогда и только тогда, когда 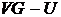– независимое множество.

В частности, отсюда следует, что 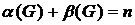для любого графа G с n вершинами.

Таким образом, все три задачи тесно связаны друг с другом. Далее рассмотрим задачу о независимом множестве.

Пусть G – граф, в котором требуется найти наибольшее независимое множество. Выберем в нем произвольную вершину а и пусть А – множество всех вершин графа, смежных с а, В – множество всех вершин, не смежных с а. Обозначим через подграф, получающийся удалением из графа G вершины а, а через подграф, получающийся удалением из G всех вершин множества 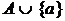. 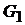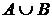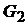Иначе говоря, – подграф графа G, порожденный множеством , а – подграф, порожденный множеством B (см. рисунок 19).

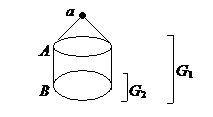
Рис. 19

Пусть Х – какое-нибудь независимое множество графа G. Если оно не содержит вершину а, то оно является независимым множеством графа 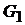, если же 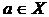, то множество 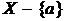является независимым множеством графа 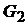. Таким образом, задача о независимом множестве для графа G свелась к решению той же задачи для двух графов меньшего размера. Это приводит к рекуррентному уравнению для числа независимости:

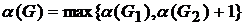
и к рекурсивному алгоритму для нахождения наибольшего независимого множества графа G: найдем наибольшее независимое множество 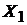графа 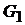, затем наибольшее независимое множество 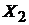графа 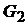и выберем большее из множеств 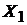и 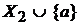. В целом процесс решения задачи можно при этом интерпретировать как исчерпывающий поиск в возникающем дереве подзадач, т.е. подграфов. Каждой вершине этого дерева соответствует некоторый граф, сыновьям вершины – два подграфа этого графа, корню – исходный граф. Листьям дерева соответствуют графы, для которых задача решается непосредственно, без сведения к подзадачам. В простейшем случае это могут быть графы с пустым множеством вершин, но при этом количество листьев будет максимальным. Можно доводить разложение на подзадачи до графов с пустым множеством ребер, при этом листьев в дереве станет меньше, но потребуется для каждого встречающегося графа проверять наличие в нем ребер. Число листьев зависит от того, в каком порядке рассматриваются вершины графа, но оно во всяком случае не меньше, чем число максимальных независимых множеств у графа, так как каждое из этих множеств будет соответствовать некоторому листу. Так, для графа 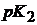, т.е. графа, состоящего из p компонент связности, каждая из которых изоморфна графу 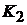, в дереве подзадач будет в лучшем случае 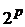листьев.

Паросочетания

Паросочетанием в графе называется множество ребер, попарно не имеющих общих вершин. Задача о паросочетании состоит в том, чтобы в данном графе найти паросочетание с наибольшим числом ребер. Это число для графа G будем обозначать через 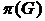. Реберным покрытием графа называется такое множество ребер, что всякая вершина графа инцидентна хотя бы одному из этих ребер. Наименьшее число ребер в реберном покрытии графа G обозначим через 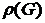. Заметим, что реберное покрытие существует только для графов без изолированных вершин.

Определение паросочетания похоже на определение независимого множества вершин, паросочетание иногда так и называют – независимое множество ребер. Эта аналогия усиливается еще тесной связью между реберными покрытиями и паросочетаниями, подобно тому, как связаны между собой вершинные покрытия и независимые множества. Даже равенство, количественно выражающее эту связь, имеет точно такой же вид (напомним, что числа независимости 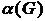и вершинного покрытия 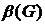связаны равенством 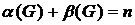). Приведем доказательство этого факта, так как оно имеет алгоритмическое значение – показывает, как каждая из двух задач сводится к другой.

Теорема 11.Для любого графа G с n вершинами, не имеющего изолированных вершин, справедливо равенство .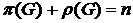

Доказательство. Пусть М – наибольшее паросочетание в графе G. Обозначим через W множество всех вершин графа, не покрытых ребрами этого паросочетания. Тогда 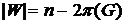. Очевидно, W – независимое множество (иначе М не было бы наибольшим). Выберем для каждой вершины из М какое-нибудь инцидентное ей ребро. Пусть F – множество всех выбранных ребер. Тогда 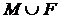– реберное покрытие и 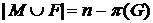, следовательно, .

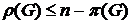Обратно, пусть С – наименьшее реберное покрытие графа G. Рассмотрим подграф Н графа G, образованный ребрами этого покрытия. В графе Н один из концов каждого ребра является вершиной степени 1 (ребро, каждая вершина которого инцидентна по крайней мере еще одному ребру, можно было бы удалить из С, оставшиеся ребра по-прежнему покрывали бы все вершины). Отсюда следует, что каждая компонента связности графа Н является звездой (звезда – это дерево, у которого не более одной вершины степени больше 1). Так как в любом лесе сумма количеств ребер и компонент связности равна числу вершин, то число компонент связности в графе Н равно 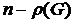. Выбрав по одному ребру из каждой компоненты, получим паросочетание. Отсюда следует, что . 

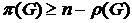Пусть G – граф, М – некоторое паросочетание в нем. Ребра паросочетания будем называть сильными, остальные ребра графа – слабыми. Вершину назовем насыщенной, если она инцидентна какому-либо ребру паросочетания, в противном случае ненасыщенной,. На рисунке 20 слева показан граф и в нем выделены ребра паросочетания 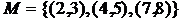. Вершины 1 и 5 – ненасыщенные. Заметим, что к этому паросочетанию нельзя добавить ни одного ребра, т.е. оно максимальное. Однако оно не является наибольшим. В этом легко убедиться, если рассмотреть путь 5,6,8,9,10,7,3,4 (показан пунктиром). Он начинается и оканчивается в ненасыщенных вершинах, а вдоль пути чередуются сильные и слабые ребра. Если на этом пути превратить каждое сильное ребро в слабое, а каждое слабое – в сильное, то получится новое паросочетание, показанное на рисунке справа, в котором на одно ребро больше. Увеличение паросочетания с помощью подобных преобразований – в этом и состоит суть метода чередующихся цепей.

Рис.20

Сформулируем необходимые понятия и докажем теорему, лежащую в основе этого метода чередующихся цепей. Чередующейся цепью относительно данного паросочетания называется простой путь, в котором чередуются сильные и слабые ребра (т.е. за сильным ребром следует слабое, за слабым – сильное). Чередующаяся цепь называется увеличивающей, если она соединяет две ненасыщенные вершины. Если М – паросочетание, Р – увеличивающая цепь относительно М, то легко видеть, что 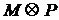– тоже паросочетание и .

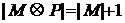Теорема 12. Паросочетание является наибольшим тогда и только тогда, когда относительно него нет увеличивающих цепей.

Доказательство. Если есть увеличивающая цепь, то, поступая так, как в рассмотренном примере, т.е. заменяя вдоль этой цепи сильные ребра на слабые и наоборот, мы, очевидно, получим большее паросочетание. Для доказательства обратного утверждения рассмотрим паросочетание М в графе G и предположим, что М не наибольшее. Покажем, что тогда имеется увеличивающая цепь относительно М. Пусть 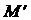– другое паросочетание и 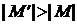. Рассмотрим подграф Н графа G, образованный теми ребрами, которые входят в одно и только в одно из паросочетаний 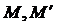. Иначе говоря, множеством ребер графа Н является симметрическая разность 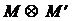. В графе Н каждая вершина инцидентна не более чем двум ребрам (одному из М и одному из 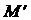), т.е. имеет степень не более двух. В таком графе каждая компонента связности – путь или цикл. В каждом из этих путей и циклов чередуются ребра из М и 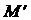. Так как 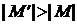, то имеется компонента, в которой ребер из 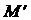содержится больше, чем ребер из М. Это может быть только путь, у которого оба концевых ребра принадлежат 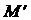. Легко видеть, что относительно М этот путь будет увеличивающей цепью. 

Для решения задачи о паросочетании остается научиться находить увеличивающие цепи или убеждаться, что таких нет. Тогда, начиная с любого паросочетания (можно и с пустого множества ребер), можем строить паросочетания со все увеличивающимся количеством ребер до тех пор, пока не получим такое, относительно которого нет увеличивающих цепей. Оно и будет наибольшим. Известны эффективные алгоритмы, которые ищут увеличивающие цепи для произвольных графов, но они достаточно сложны. Рассмотрим более простой алгоритм, решающий эту задачу для двудольных графов.

Пусть 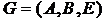– двудольный граф, М – паросочетание в G, X и Y – множества ненасыщенных вершин соответственно в долях А и В. Всякая увеличивающая цепь, если такая имеется, соединяет вершину из А с вершиной из В. Ориентируем ребра графа G следующим образом: всякое слабое ребро в направлении от А к В, а всякое сильное – в направлении от В к А. Полученный орграф обозначим через 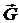. Очевидно, что увеличивающая цепь в графе G существует тогда и только тогда, когда в графе 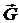имеется ориентированный путь из какой-либо вершины 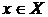в какую-либо вершину 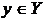. Такой путь можно найти (или убедиться в его отсутствии) простым поиском в ширину.

Оптимальные каркасы

Задача об оптимальном каркасе (стягивающем дереве) состоит в следующем. Дан обыкновенный граф 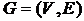и весовая функция на множестве ребер 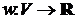. Вес множества 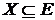определяется как сумма весов составляющих его ребер. Требуется в графе G найти каркас максимального веса. Обычно рассматривают задачу на минимум, но это не существенно – она преобразуется в задачу на максимум, если заменить функцию w на -w. В этом разделе будем предполагать, что граф G связен, так что решением задачи всегда будет дерево.

Для решения задачи об оптимальном каркасе известно несколько жадных алгоритмов. Рассмотрим один из них, известный под названием алгоритм Прима. В этом алгоритме на каждом шаге рассматривается частичное решение задачи, представляющее дерево. Вначале это дерево состоит из единственной вершины, в качестве этой вершины может быть выбрана любая вершина графа. Затем к дереву последовательно добавляются ребра и вершины, пока не получится остовное дерево, т.е. каркас. Для того, чтобы из текущего дерева при добавлении нового ребра опять получилось дерево, это новое ребро должно соединять вершину дерева с вершиной, еще не принадлежащей дереву. Такие ребра будем называть подходящими относительно рассматриваемого дерева. «Жадность» алгоритма состоит в том, что на каждом шаге из всех подходящих ребер выбирается ребро наименьшего веса. Это ребро вместе с одно новой вершиной добавляется к дереву. Если обозначить через U и F множества вершин и ребер строящегося дерева, а через W множество вершин, еще не вошедших в это дерево, то алгоритм Прима можно представить следующим образом.

Алгоритм 1.Построение оптимального каркаса методом Прима

1 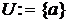, где a – произвольная вершина графа

2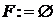

3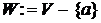

4 while 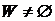do

5 найти ребро наибольшего веса 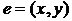среди всех таких ребер, у которых ,

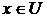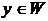
6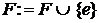

7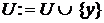

8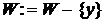

Докажем, что алгоритм Прима на самом деле строит оптимальный каркас. Дерево F назовем фрагментом, если оно является подграфом графа G и существует такой оптимальный каркас 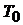графа G, что F является подграфом графа .

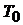Теорема 13. Если F – фрагмент, е – подходящее ребро наибольшего веса относительно F, то 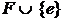– фрагмент.

Доказательство. Пусть 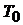– оптимальный каркас, содержащий F в качестве подграфа. Если ребро е принадлежит 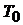, то 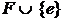– подграф 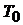и, следовательно, фрагмент. Допустим, е не принадлежит 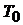. Если добавить ребро е к дереву 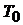, то образуется цикл. В этом цикле есть еще хотя бы одно подходящее ребро относительно F (никакой цикл, очевидно, не может содержать единственное подходящее ребро). Пусть 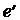– такое ребро. Тогда подграф 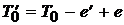, получающийся из 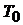удалением ребра 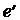и добавлением ребра е, тоже будет деревом. Так как 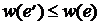, то . 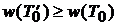Но 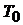– оптимальный каркас, следовательно, 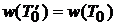и 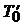– тоже оптимальный каркас. Но 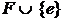является подграфом графа 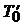и, следовательно, фрагментом. 

Дерево, состоящее из единственной вершины, очевидно, является фрагментом. Из теоремы 13 следует, что если после некоторого количества шагов алгоритма Прима дерево F является фрагментом, то оно будет фрагментом и после следующего шага. Следовательно, и окончательное решение, полученное алгоритмом, будет фрагментом, т.е. оптимальным каркасом.