Итоговая контрольная работа 10 класс.
А1 Вычислите: 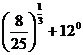 1)12
1)12 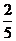 ; 2) 1
; 2) 1 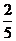 ; 3)3
; 3)3 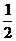 ; 4) 2
; 4) 2 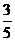 .
.
А2 Упростите выражение: 5 – 8sin2320 – 8cos2320
1) – 3 cos 640; 2) 5 – 8cos 640; 3) 13; 4) – 3.
A3 Упростите выражение: 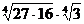
1) 6; 2) 2 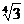 ; 3) 12; 4) 6
; 3) 12; 4) 6 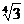 .
.
А4 Найдите значение выражения: 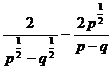 при p = 8, q = 9
при p = 8, q = 9
1) 4 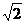 ; 2) – 6; 3) - 4
; 2) – 6; 3) - 4 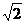 ; 4) 6.
; 4) 6.
A5Решите неравенство: 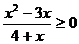
1) (–∞; - 4 )U[0;3]; 2) ( - 4; 0]U[3; +∞); 3) [3; +∞); 4) (–∞; - 4 ).
A6Решите уравнение: sinx – cos2x = sin2x
1) 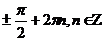 ; 2)
; 2) 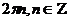 ; 3)
; 3) 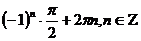 ; 4)
; 4) 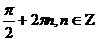 .
.
А7 Тело движется прямолинейно по закону 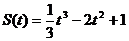 (расстояние измеряется в метрах). Вычислите скорость движения в момент времени t = 4 сек.
(расстояние измеряется в метрах). Вычислите скорость движения в момент времени t = 4 сек.
1) 1 м/с; 2) 0 м/с; 3) 32 м/с; 4) – 9 м/с.
|
 f ' (-2), если f (x) = (7x + 12 )3
f ' (-2), если f (x) = (7x + 12 )3 1) – 12; 2) 28; 3) 12; 4) 84.
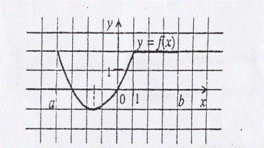
А9 Укажите промежутки возрастания функции
у = f(x), заданной графиком на отрезке [a; b].
1) [a; - 1,5]; 2) [1; b];
3) [- 1,5; 1]; 4) [0; 1].
|
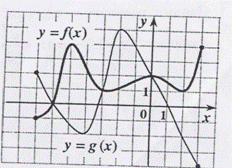
на промежутке [- 7; 3 ]. Укажите те значения х,
при которых f (x) 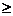 g (x).
g (x).
1)[- 7; - 6] U [- 3; 0];
2)[- 6; - 3] U [ 0; 3];
3)[ - 7; - 4] U [ - 2; 3];
4)[ - 7; - 5] U [ - 3; 0] U [ 2; 3].
В1 Упростите выражение: 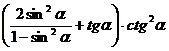
В2 Сколько корней имеет уравнение: 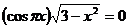
|
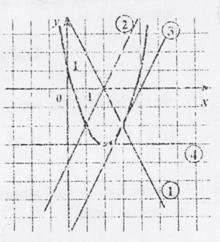
f (x) = ax2 + bx + c и четыре прямые. Одна
из этих прямых – график производной
данной функции. Укажите номер этой прямой.
В4 При каком наибольшем значении а функция
f (x) = 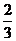 x3 – ax2 + ax + 7 возрастает на всей
x3 – ax2 + ax + 7 возрастает на всей
числовой прямой?
В5 Найдите максимум функции
У = 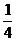 + 3х – х2 -
+ 3х – х2 - 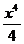
В6Найдите разность между наибольшим и наименьшим значениями функции
У = 5,2 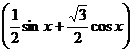
С1Решите уравнение 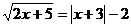
С2 Найдите множество значений функции у = cos2x, если х 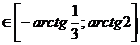
С3 Найдите все целые значения выражения
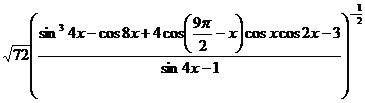
С4 Найдите целые корни уравнения: ( 6 – х )∙( х – 2 )∙( х + 3 )∙( х + 9 ) = 24х2
Контрольная работа по теме: Первообразная и интеграл. 11класс.
Вариант.
A1 Определите функцию, для которой F(x) = x2 – sin2x – 1 является первообразной:
1) f(x) = 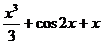 ; 2) f(x) = 2x – 2cos2x; 3) f(x) = 2x +
; 2) f(x) = 2x – 2cos2x; 3) f(x) = 2x + 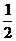 cos2x; 4) f(x) =
cos2x; 4) f(x) = 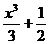 cos2x + x.
cos2x + x.
A2 Найдите первообразную для функции. F (x) = 4х3 + cos x
1) F(x) = 12x2 – sinx + c; 2) F(x) = 4x3 + sinx + c; 3) F(x) = x4 – sinx + c; 4) F(x) = x4 + sinx + c.
A3 Для функции f(x) = х2 найдите первообразную F, принимающую заданное значение в заданной точке F (- 1) = 2
1) F(x) = 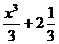 ; 2) F(x) = 2x +
; 2) F(x) = 2x + 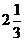 ; 3) F(x) = –
; 3) F(x) = – 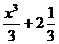 ; 4) F(x) =
; 4) F(x) = 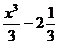 .
.
A4 Точка движется по прямой так, что её скорость в момент времени t равна V (t) = t + t2. Найдите путь, пройденный точкой за время от 1 до 3 сек, если скорость измеряется в м /сек. 1) 18 м; 2) 12 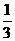 м; 3) 17
м; 3) 17 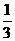 м; 4) 20 м.
м; 4) 20 м.
А5 Вычислите 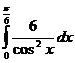 1) 6
1) 6 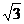 ; 2) 6; 3) 2
; 2) 6; 3) 2 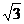 ; 4) 3
; 4) 3 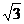 .
.
А6 Найдите площадь криволинейной трапеции, ограниченной линиями у = – х2 + 3 и у = 0
1) 4 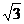 ; 2) 6
; 2) 6 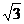 ; 3) 9
; 3) 9 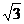 ; 4) 8
; 4) 8 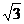 .
.
А7 Найдите площадь фигуры, ограниченной линиями у = 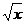 и у =
и у = 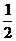 х
х
1) 2; 2) 1 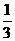 ; 3) 2
; 3) 2 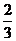 ; 4) 1
; 4) 1 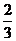 .
.
А8 Вычислите площадь фигуры, ограниченной графиком функции у = 2 – х2, касательной к этому графику в его точке с абсциссой х = - 1 и прямой х = 0
1) 1 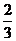 ; 2) 2
; 2) 2 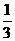 ; 3)
; 3) 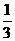 ; 4) 1
; 4) 1 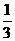 .
.
В1 Вычислите 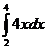
В2 Найдите сумму абсцисс точек пересечения графиков функции у = (х – 1)(х + 2) и её первообразной, если одна из этих точек находится на оси ординат.
С1 Найдите ту первообразную функции f(x) = 3х – 1 , для которой уравнение F(x) = 5 имеет единственный корень.
Контрольная работа по теме: Первообразная и интеграл. 11класс.
Вариант.
А1 Определите функцию, для которой F(x) = – cos 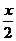 - x3 + 4 является первообразной:
- x3 + 4 является первообразной:
1) f(x) = - sin 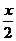 - 3x2; 2) f(x) =
- 3x2; 2) f(x) = 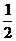 sin
sin 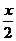 - 3x2; 3) f(x) = -
- 3x2; 3) f(x) = - 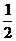 sin
sin 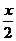 - 3x2; 4) f(x) = 2sin
- 3x2; 4) f(x) = 2sin 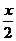 - 3x2 .
- 3x2 .
A2Найдите первообразную для функции f(x) = x2 – sinx
1) F(x) = 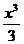 - cos x + c; 2) F(x) = 2x – cosx + c; 3) F(x) =
- cos x + c; 2) F(x) = 2x – cosx + c; 3) F(x) = 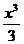 + cosx + c; 4) F(x) =
+ cosx + c; 4) F(x) = 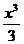 + sinx + c.
+ sinx + c.
A3 Для функции f(x) = 2x - 2 найдите первообразную F, график которой проходит через точку А(2;1)
1) F(x) = - х2 – 2х – 1; 2) F(x) = х2 + 2х + 2; 3) F(x) = 2х2 – 2; 4) F(x) = х2 – 2х + 1.
А4Точка движется по прямой так, что её скорость в момент времени t равна V (t) =3 + 0,2 t. Найдите путь, пройденный точкой за время от 1 до 7 сек., если скорость измеряется в м /сек
1) 22, 8 м; 2)29 м; 3) 23 м; 4) 13 м.
А5Вычислите 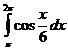 1)
1) 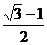 ; 2) 3
; 2) 3 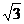 - 3; 3) 0; 4) 3 - 3
- 3; 3) 0; 4) 3 - 3 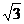 .
.
А6 Найдите площадь криволинейной трапеции, ограниченной линиями у = 2х2, у = 0, х = 2
1) 5 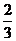 ; 2) 2
; 2) 2 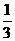 ; 3) 5
; 3) 5 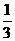 ; 4) 2
; 4) 2 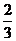 .
.
А7 Найдите площадь фигуры, ограниченной линиями у = 5 – х2 , у = 1
1) 16; 2) 5 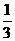 ; 3)11
; 3)11 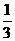 ; 4) 10
; 4) 10 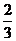 .
.
А8 Вычислите площадь фигуры, ограниченной графиком функции у = – х2 + 3, касательной к этому графику в его точке с абсциссой х = 1 и прямой х = 0.
1) 2 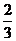 ; 2)
; 2) 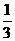 ; 3) 2
; 3) 2 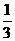 ; 4)
; 4) 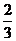 .
.
В1 Вычислите 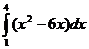
В2Найдите сумму абсцисс точек пересечения графиков функции у = (х – 3)(х + 2) и её первообразной, если одна из этих точек находится на оси ординат.
С1Найдите ту первообразную функции f(x) = 2х + 5 , для графика которой прямая у = 7х – 3 является касательной.