Решение задач оптимизации в Excel
Если вы научились строить математические модели задач линейного программирования, но не умеете аккуратно проводить вычисления, особенно в дробях, либо задача имеет не очень простую по структуре модель, то можно использовать специальную надстройку Excel "Поиск решения", которая позволяет решать задачи на поиск оптимального значения целевой функции. Надстройка вызывается из менюСервис,пункт Поиск решения.Если в меню Сервис нет такого пункта, то можно установить его, выполнив команду Сервис | Надстройки.В окне диалога "Надстройки" установите флажок на строке Поиск решенияи нажмите OK.
Рассмотрим задачу, аналогичную задаче 8 (о плане). Пусть условие задачи записано в таблице на листе Excel. Модель задачи имеет вид:
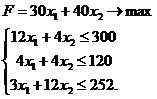
Для решения задачи заполните лист Excel, выполнив следующие действия:
1. Определим ячейки для хранения переменных В7 и С7 (изменяемые ячейки), первоначально зададим им нулевые значения.
2. Определим ячейку для целевой функции В8, введем в нее формулу, определяющую целевую функцию. Не забудьте, любая формула в Excel начинается со знака «=».
3. Введем в ячейки А14:А16 левые части формул ограничений. Если использовать абсолютные ссылки на изменяемые ячейки, то формулу можно ввести один раз и копировать, используя маркер заполнений. Каждый раз при нажатии на enter формулы пересчитываются и в ячейке стоит значение 0.
4. Теперь все готово для вызова мастера Поиск решения из меню Сервис.
5. Аккуратно заполните поля ввода для целевой функции, изменяемых ячеек. Активизируйте кнопку Равной максимальному значению. (Если бы задача была на поиск минимального значения, то Равной минимальному значению). В поле ввода Изменяя ячейки введите В7:С7 и нажмите на кнопку Добавить в окне Ограничения.
6. Окно сворачивается в строку, состоящую из трех полей ввода. В первое поле вводим ссылаемся на ячейку первого ограничения, во-втором выбираем знак «£» , в третьем ссылаемся на ячейку, содержащую правые части ограничения, можно ввести цифрой, но удобнее сослаться. Команда Добавитьочищает поля для ввода следующего ограничения. Не забудьте ввести условия неотрицательности для изменяемых ячеек и целостности, если в этом есть необходимость по смыслу задачи. После ввода всех ограничений нажмите «ОК» (см. рис. 4.1).
7. Кнопка Выполнить на форме позволяет запустить процесс поиска решения. Можно предварительно установить нужные параметры поиска, кнопка Параметры.
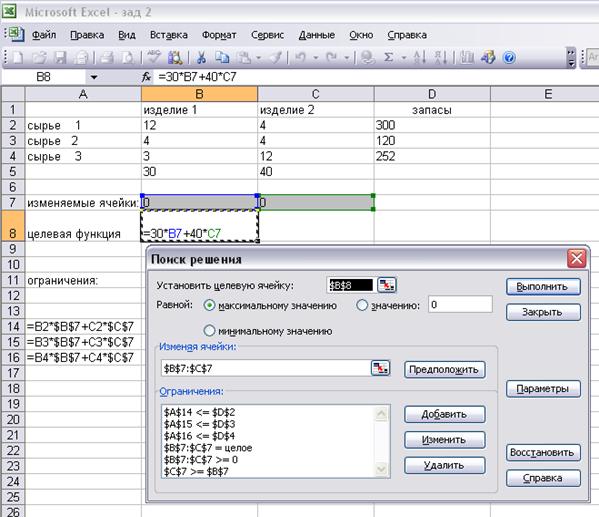
Рис. 4.1Пример оформления задачи и ввода первоначальных данных
8. Получаем сообщение Решение найдено.На листеExcel в изменяемых ячейках и целевой будут находиться оптимальные решения задачи. Удобно запросить отчет по результатам (см. рис. 4.2). В автоматически сформированном отчете кроме значений переменных и целевой функции, каждому ограничению присваивается статус «связанное» или «несвязанное», что характеризует дефицитность ресурса. Если ограничение несвязанное, то соответствующий ресурс не является дефицитным, имеется в избытке, в графе разница явно указан излишек. Если ограничение связанное, то ресурс дефицитен, излишков нет.
Можно проводить более тонкий экономический анализ с помощью других двух отчетов: по пределам и по устойчивости. Например, выяснить предельные относительные цены на ресурсы (теневые цены) и определить какие из ресурсов являются более дефицитными. Можно узнать в каких пределах можно изменять правые части ограничений, чтобы найденное решение оставалось оптимальным.
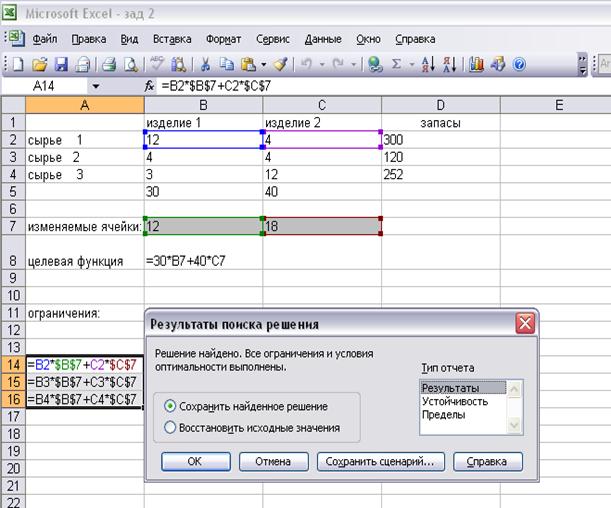
Рис.4.2.Окно диалога "Результаты поиска решений"
Замечание.
Транспортную задачу также можно решить с помощью Поиск решения.При этом в качестве изменяемых ячеек будут элементы матрицыперевозок X = (xij). Целевая функция исследуется на минимум, а ограничения в сбалансированной задаче имеют вид равенств.
Библиографический список
1. Кремер, Н.Ш. Исследование операций в экономике: учебн. пособие / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, И.М. Фридман. – М.: Банки и Биржи, 1997. – 407 с.
2. Солодовников, А.С. Математика в экономике: учебник /А.С. Солодовников, В.А. Бабийцев, А.В. Браилов, – М.: Финансы и математика
3. Шелобаев, С.И. Математические методы и модели в экономике, финансах, бизнесе: учеб.пособ. для вузов.– М.: ЮНИТИ-ДАНА, 2000. – 367 с.
4. Кузнецов, А.В. Сборник задач по математическому программированию./А. В. Кузнецов, Г. И. Новикова, Н.И. Холод. – М: Высш. школа, 1985.– 143с.
5. Бережная, Е.В. Математические методы моделирования экономических систем: уч. пособ./ Е.В. Бережная, В.И. Бережной. – М: Финансы и статистика, 2006. – 432 с.
6. Таха Х. Введение в исследование операций: – М: Мир, 1985. Кн.1.
7. Кораблин, М.А. Информатика поиска управленческих решений./М.А. Кораблин. – М: СОЛОН-Пресс, 2003. – 192 с.
Оглавление
ГЛАВА I. 3
Введение в математическое моделирование. 3
§ 1.1 Понятие математической модели, классификация моделей, виды моделирования. 3
§ 1.2. Введение в линейное программирование. 6
ГЛАВА II. 9
Основные типы задач линейного программирования и методы решения 9
§ 2.1 Построение математических моделей задач ЛП.. 9
§ 2.2 Графический способ решения систем линейных неравенств. 16
§ 2.3 Решение задачи линейного программирования графически. 19
§ 2.4 Каноническая форма задач ЛП.. 23
§ 2.5 Идея симплексного метода. 25
§ 2.6 Симплексный метод решения задач линейного программирования. 29
§ 2.7 Поиск первоначального опорного плана. 36
§ 2.8 Двойственность в линейном программировании. 38
§ 2.9 Теоремы двойственности. 42
§ 2.10 Экономическая интерпретация двойственной задачи. 45
и теории двойственности. 45
ГЛАВА III. 48
Транспортные задачи линейного программирования.. 48
§ 3.1 Постановка транспортной задачи общего вида. 48
§3.2 Алгоритм метода потенциалов. 50
§ 3.3 Усложненные задачи транспортного типа. 58
§ 4. Решение задач оптимизации в Excel 61
