IV этап. Выписывание оптимального решения.
Если симплекс-метод остановился согласно пункту 1 II этапа, то решение задачи выписывается следующим образом. Базисные переменные принимают значения столбца правых частей соответственно. В нашем примере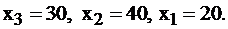 
Свободные переменные равны 0: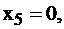 
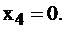Значение целевой функции равно числу в правом нижнем углу таблицы: 
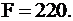Итак, 
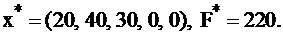
Ответ к задаче: необходимо в план выпуска включить 20 изделий типа А, 40 изделий типа В, при этом прибыль будет максимальной и составит 220 руб. Переменная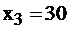 
означает, что есть излишки по первому ограничению в количестве 30 ед., по смыслу этой задачи – это потенциальная возможность выпуска.
Внимательный читатель должен заметить абсолютное сходство таблиц решенной выше задачи с системами уравнений, получаемыми при переходе от одного базиса к другому в § 2.5. Мы решали одну и ту же задачу одним и тем же методом. Только в этом параграфе вычисления были более организованы и оформлены в таблицу, правила пересчета, выбора разрешающего элемента, критерии остановки вытекают из идей, сформулированных в §2.5. Строгого доказательства соответствия идей алгоритму в этом пособии не приводим. Это дело математиков, а не экономистов. Нашей целью является построение моделей, понимание идей и умение применять готовые алгоритмы.
Для удобства решения задач приведем блок-схему алгоритма симплекс-метода, которая в точности повторяет этапы, и возможно для некоторых читателей будет более удобна в пользовании, т.к. стрелочки указывают четкую направленность действий, смотри рис.2.7. Ссылки в блок-схеме показывают, к какому этапу или подпункту относится соответствующая группа преобразований.
 |
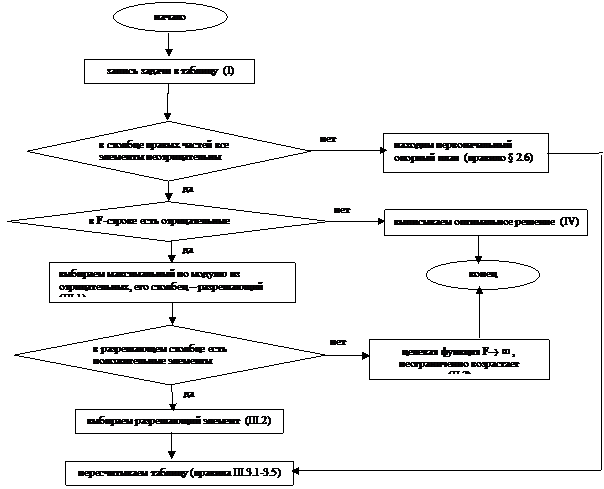Рис. 2.7 Блок-схема алгоритма симплекс-метода
В конце этого параграфа приведем примеры задач для самостоятельного решения. Задачи имеют общее условие, а исходные данные выбираются согласно варианту. Построить математическую модель задачи, решить графически и симплекс-методом.
6.1. Организации, занимающейся перевозкой продукции, необходимо арендовать железнодорожные контейнеры: 5-тонные и 7-тонные.5-тонных имеется в наличии не более а штук, 7-тонных не более в. Аренда 5-тонного стоит 2 тыс.руб, 7-тонного – 3 тыс.руб., всего по смете выделено N тыс.руб. Определить сколько контейнеров каждого вида следует арендовать, чтобы общий объем грузоперевозок был максимальным.
| № вар | ||||||||||||||||||||
| а | ||||||||||||||||||||
| в | ||||||||||||||||||||
| N |
6.2. Составить модель задачи ЛП, решить ее.
Туристическая фирма предлагает два вида путевок: шоп-туры и туры для отдыха. Фирма гарантирует получение виз не более N туристам. Туристы, едущие в шоп-туры, размещаются в гостинице в 4-местные номера, а купившие туры для отдыха – в 2-местные. Количество 4-местных номеров, забронированных фирмой не более a, а количество 2-местных не более в. Фирма получает прибыль от продажи одного шоп-тура 60$, а тура для отдыха – 100$. Какое количество путевок каждого вида надо продать фирме, чтобы полученная от продажи прибыль была максимальной?
| № вар | ||||||||||||||||||||
| а | ||||||||||||||||||||
| в | ||||||||||||||||||||
| N |
§ 2.7. Поиск первоначального опорного плана
Предположим, что каноническая задача ЛП имеет опорный план недопустимый – правые части уравнений системы ограничений отрицательны.
Этот случай возникает, например, при решении задачи о смесях и раскрое. Канонический вид задачи, рассмотренной в § 2.3 (7), выглядит так:
.
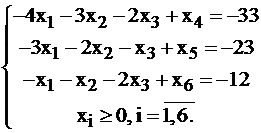
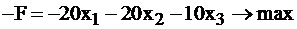Запишем задачу в симплекс-таблицу (табл.2.9):
Таблица 2.9
| базисные | 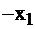 | 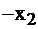 | 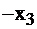 | правые части |
 |  |  |  |   |
 | | |  |  |
 | | | |   |
 |  | |  |  |
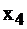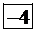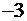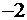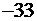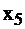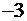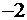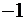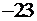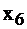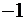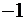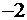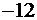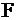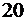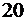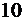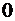Базисное решение, соответствующее базису 
и равное (0; 0; 0; -33; -23; -12), не является допустимым ввиду отрицательности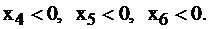 
Сформулируем правило нахождения допустимого первоначального опорного плана:
Если в столбце свободных членов есть отрицательныеэлементы, выберите из них наибольший по модулю, а в его строке любой отрицательный. Взяв этот элемент в качестве разрешающего, пересчитайте таблицу по прежним правилам 3.1–3.5.
Если в полученной таблице все элементы столбца свободных членов стали положительны, либо равны 0, то данное базисное решение можно взять в качестве первоначального опорного плана. Далее дорешать задачу симплекс-методом. Если в столбце свободных членов не все элементы неотрицательны, то еще раз воспользоваться этим правилом.
Применим правило для задачи о рационе. В качестве разрешающей строки табл.2.9 нужно выбрать первую. А разрешающим элементом выберем, к примеру, элемент -4. Заметим, что строка определяется по правилу однозначно, т.к.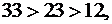 
а выбор разрешающего элемента имеет некоторую степень свободы.
Таблица 2.10
| базисные | 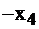 | 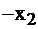| 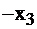| свободные |
 | –  |  |  |  |
| |  | | |  |
| |  | |  |   |
| |  | | |  |
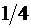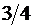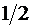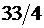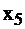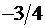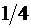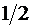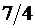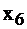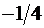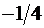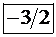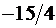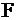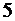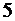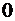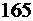Переменная вошла в базис вместо 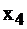(все вычисления осуществлялись по правилу 3.2–3.5). В правом столбце еще остался отрицательный элемент, воспользуемся правилом еще раз. Строка переменной 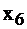– разрешающая, а в качестве разрешающего элемента возьмем, к примеру 
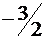. Получим таблицу 2.11 . Таблица 2.11
| базисные | 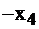| 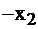| 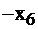 | свободные |
| |  |  |  |  |
| |  |  | |  |
 | | |  |  |
| | | | | |
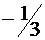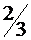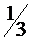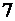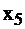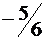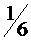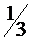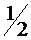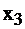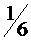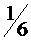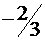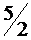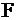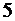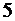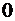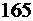Полученный базисный план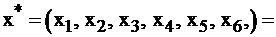 
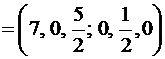является допустимым, и к тому же оказывается оптимальным, т.к. в индексной строке нет отрицательных элементов. Оптимальное значение целевой функции F*=165. Действительно,
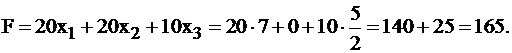
В этой задаче не пришлось улучшать найденный первоначальный опорный план, т.к. он оказался оптимальным. Иначе мы должны были вернуться к III этапу.