Базисным называется решение, соответствующее нулевым значениям свободных переменных.

В качестве базисных можно было взять и другие переменные – 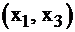или .

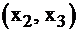Как переходить от одного базиса 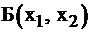к другому базису ?

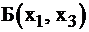Для этого надо переменную 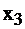перевести в базисные, а 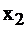– в небазисные. То есть в уравнениях надо 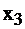выразить через 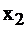и подставить в 1-е уравнение:

,

.

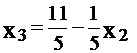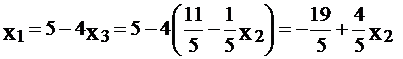Базисное решение, соответствующее базису 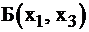, таково: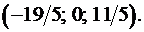

Если теперь от базиса 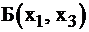нам захочется перейти к базису 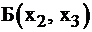, то

,

.

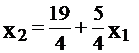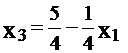Базисное решение, соответствующее базису 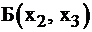: (0;19/4;5/4).

Из трех найденных базисных решений решение, соответствующее базису 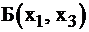, отрицательное ( 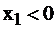). Нас в ЗЛП интересуют только неотрицательные решения. Если задача ЛП имеет решение, то оно достигается на множестве базисных неотрицательных решений системы ограничений канонической формы.

Поэтому идея симплекс-метода и состоит в последовательном переходе от одного базиса к другому, лучшему с точки зрения значения целевой функции.

Рассмотрим пример.

Решим задачу ЛП:

Функцию 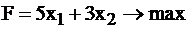необходимо максимизировать, при заданной системе ограничений:

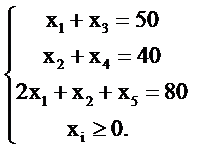
Эти ограничения могут рассматриваться как произошедшие из неравенств, а переменные 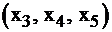– как дополнительные. Запишем ограничения, выбрав базис из переменных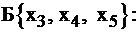

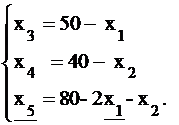
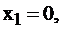
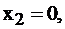
Этому базису соответствует базисное неотрицательное решение 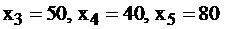или (0; 0; 50; 40; 80).

Теперь нужно выразить F через небазисные переменные, в нашем случае это уже сделано: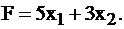

1. Проверим, достигла ли функция F своего максимального значения. Для этого базисного решения 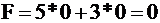– значение функции равно 0. Но его можно увеличить, если будет возрастать, т. к. коэффициент в функции при положителен. Причем, т.к. 5>3, то при увеличении функция будет расти быстрей, чем при увеличении 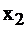. До каких пор мы можем увеличивать переменную ? При увеличении значения переменных 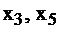уменьшаются (смотрите 1-е и 3-е равенства системы ограничений). Переменная не может быть увеличена больше чем до 50, иначе 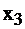станет отрицательной (ввиду равенства 1); и не больше чем до 40, иначе 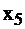станет отрицательна. Итак, из анализа следует, что переменную можно увеличить до 40, что гарантирует увеличение F.

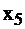2. Перейдем к новому базису Б₂, введя переменную в базис вместо . Итак, 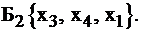Выразим эти базисные переменные через небазисные. Для этого, сначала выразим из 3-го уравнения и подставим в остальные, в том числе и в функцию.

Имеем:

.

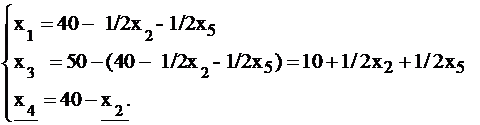
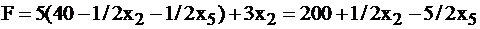Базисное решение, соответствующее базису 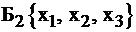, имеет вид (40; 0; 10; 40; 0) и функция F принимает значение, равное 200 в этом базисе.

3. Значение функции F можно ещё увеличить за счет переменной 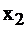, т.к. коэффициент при ней положителен. Из первого уравнения видно, что 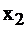можно увеличить до 80, из третьего – до 40, второе уравнение позволяет увеличивать без ограничений. Следовательно, всего до 40. Вводим 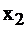в базис из третьего уравнения вместо .

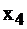Имеем:

.

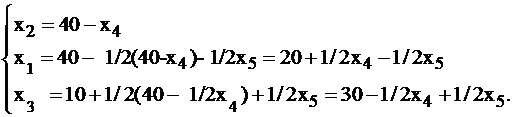
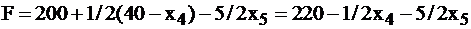4. Значение функции нельзя больше увеличивать, т.к. коэффициенты при переменных 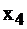и 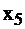в функции отрицательны. При любых положительных значениях этих переменных значение функции будет меньше 200. Следовательно, необходимо, чтобы эти переменные были равны 0, тогда значение будет максимальным и равно 220. При этом базисные переменные .

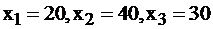Пример завершен.

На этом примере наглядно продемонстрирована идея метода. Постепенно переходя от базиса к базису, при этом, всегда обращая внимание на значения целевой функции, которые должны улучшиться, мы приходим к такому базису, в котором значение целевой функции улучшить нельзя, оно оптимально. Заметим, что базисов конечное число, поэтому количество шагов, совершаемых нами до нужного базиса, конечно. Осталось эту идею воплотить в четкий алгоритм, чтобы избежать тяжелого вычислительного процесса, и отдать полученный в результате симплекс-метод на «вооружение» машине-компьютеру.