Введение в математическое моделирование

§ 1.1. Понятие математической модели,
классификация моделей, виды моделирования

Математические модели являются инструментальным средством описания задач самого разного класса. Причем задачи из разных областей экономики могут иметь похожие модели и решаться одинаковыми методами. Использование корректно построенной модели какого-либо процесса позволяет формализовать и описать наиболее важные связи между объектами, оценить различные параметры зависимостей, предсказывать поведение объекта, тем самым определять наилучшие решения в той или иной ситуации, оценить количественно эффективность принимаемых решений, прогнозировать их негативные последствия, использовать полученные оценки.

Математическая модель – это условный совокупный образ объекта в виде совокупности уравнений, неравенств, логических соотношений, созданный для получения новых знаний, исследования объекта, анализа и оценки принимаемых решений в конкретных или возможных ситуациях.

Моделирование – это метод исследования объектов, процессов на их моделях, построения и изучения моделей, определения и улучшения их характеристик, рационализирующих способ построения и управления.

В разных науках существуют различные способы классификации моделей. Классификация зависит от признака, лежащего в основе. Признаком может выступать: отрасль знаний, способ представления модели, учет временного фактора, учет влияния фактора случайности, приспособляемости модели и др.

По отраслям знаний модели классифицируются на биологические, социологические, физические, экономические и др. Математические модели, используемые в экономике, можно классифицировать по особенностям моделируемого объекта – на макро- и микроэкономические. Макроэкономические модели описывают экономику страны как единое целое, связывая такие макроэкономические материальные и финансовые показатели, как ВВП, потребление, инвестиции, занятость, бюджет, инфляция, ценообразование и др. Микроэкономические модели описывают состояние структурных составляющих экономики, стратегии поведения фирм в неустойчивой или стабильной среде.

По целям моделирования и используемому инструментарию модели подразделяются на теоретические и прикладные, оптимизационные и равновесные. Прикладные модели обеспечивают возможность оценки параметров функционирования конкретных технико-экономических объектов и обоснования выводов для принятия управленческих решений. Равновесные модели, присущие рыночной экономике, описывают поведение субъектов хозяйствования в стабильных устойчивых состояниях, но и в нерыночной экономике, где равновесие по одним параметрам компенсируется другими факторами. Оптимизационные модели связаны в основном с микроуровнем и предполагают выбор наилучшего варианта по некоторому критерию: максимум прибыли, минимизация расходов, минимум отходов производства и т.д. Причем различают одно- и многокритериальные задачи.

По отношению к фактору времени модели делятся на статические и динамические, непрерывные и дискретные. Статические модели описывают состояние объекта в конкретный текущий момент или период времени, а динамические модели включают взаимосвязи переменных во времени. Динамические модели в свою очередь делятся на дискретные и непрерывные, в зависимости от характера изменения процесса во времени.

По отношению к фактору случайности модели делятся на стохастические и детерминированные. Детерминированные модели предполагают жесткие функциональные связи между переменными, а стохастические модели допускают наличие случайности, используя в качестве инструмента теорию вероятностей и математическую статистику.

По назначению модели делятся на балансовые (наличие ресурсов и их использование), трендовые (развитие моделируемой системы через тенденцию развития ее показателей), оптимизационные, имитационные (машинная имитация процессов).

По способу представления модели делятся на предметные и знаковые. Предметные модели воспроизводят определенные геометрические, физические, динамические свойства объекта (глобус, карты…). Знаковые модели – это схемы, чертежи, формулы. Важнейшим видом знаковых моделей являются математические.

Применительно к техническим и естественным наукам принято различать следующие виды моделирования:

- концептуальное, при котором совокупность уже известных фактов и представлений о системе представляется с помощью специальных знаков, символов;

- физическое, при котором между объектом и оригиналом устанавливаются отношения подобия;

- структурно-функциональное, при котором моделями являются чертежи, диаграммы, таблицы, дополненные специальными правилами их преобразования и объединения;

- математическое, где модель строится средствами математики и логики;

- имитационное, при котором математическая модель объекта представляет собой способ функционирования объекта, реализованный в виде программы на ПК.

Эти виды не являются взаимоисключающими и могут применяться в комбинации.

В данном пособии будут рассматриваться математические модели экономических задач, которые относятся к классу оптимизационных, в частности задачи линейного программирования.

Основные задачи управления деятельностью человека можно отнести к классу задач распределения и оптимизации ресурсов. Например, технологический процесс можно определить как последовательность работ, которые определяют превращение сырья в продукцию, такую последовательность работ называют маршрутом, каждую операцию, входящую в маршрут, можно охарактеризовать определенными режимами обработки, управления, контроля и функционирования. Процессы функционирования объекта и технологические процессы характеризуются изменениями некоторых параметров во времени, они подразделяются на дискретные и непрерывные. Зависимости между переменными и целевые функции могут быть линейными и нелинейными.

Итак, если выделить в модели следующие элементы: исходные данные, зависимости, описывающие целевую функцию, ограничения, то элементы математических моделей могут быть представлены схемой (рис.1.1).

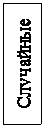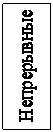Рис. 1.1 Разновидности элементов математической модели

Процесс построения и исследования модели можно представить как последовательность следующих шагов:

1) знакомство с предметной областью, прогноз или анализ процесса. Формулировка целей моделирования, уточнение круга задач. Предварительная оценка целесообразности построения модели;

2) переход от описания предметной области в содержательных терминах к формализованным описаниям: введение переменных, установления связей между объектами в виде формального текста, выбор алгоритма, технологии решения задачи;

3) выбор специального программного и аппаратного обеспечения, реализация разработанной модели программно-аппаратными средствами;

4) анализ построенной модели, оценка адекватности модели, работа с готовой моделью, выдвижение гипотез, альтернативных вариантов, принятие решений, разработка планов действий, контроль над реализацией плана.

В каждой задаче мы должны ясно определить цели, поставленные перед системой, изучить обстановку, освоиться с терминологией, процессом, определить различные способы действия, приемлемые для ситуации, дать в какой-то форме постановку задачи. Построить подходящую логическую или математическую модель, которая свяжет переменные задачи с реальными ограничениями, целями задачи, мерой эффективности. Затем, исходя из полученной модели, выбрать метод и найти решение, оптимизирующее эту меру эффективности, т.е. оптимальное решение. Последнее, сравнить это решение, полученное с помощью математической модели с действительностью, чтобы выяснить: в самом ли деле мы сформулировали и решали ту реальную задачу, с которой начали; когда меняется ситуация, какие изменения надо вносить в математическую модель; можно ли улучшить модель, что привело бы к новым решениям, более реалистичным и точным.

Одним из видов математического моделирования экономических задач является линейное программирование ­­– раздел математики, изучающий оптимизационные задачи определенного вида.