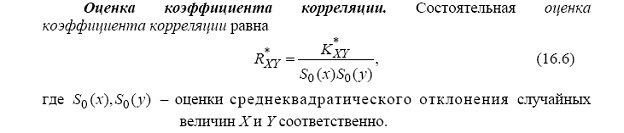Числовые характеристики случайных величин, распределенных по равномерному, показательному и нормальному законам (значения мат. ожидания и дисперсии).

1.Равномерное распределение

Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения (^ - местами, где не получилось сделать верхний индекс, этим знаком обозначена степень)

b

MX = = = | =

a b

MX² = = = | = =

a

DX = MX² – (MX)² = - = =

Среднее квадратическое отклонение

σX = =

2.Показательное распределение

Найдем математическое ожидание и дисперсию.

∞

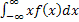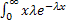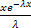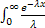MX = = dx = = λ(- | + dx =

⁰

∞

- | =

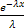Результат получен с использованием того факта, что

∞

xe^-λx | = 0

Для нахождения дисперсии найдем величину MX²

MX² = =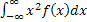

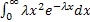
Дважды интегрируя по частям получаем

MX² =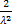

Тогда DX = MX² – (MX)² =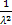

σX =

3.Нормальное распределение

Найдем математическое ожидание и дисперсию.

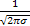
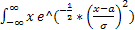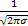
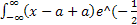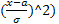MX = = *( )dx =

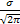
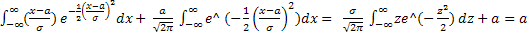
z = (x-a)/σ

Поскольку 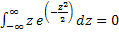как интеграл по всей прямой от нечетной функции.

Таким образом, параметр а – математическое ожидание.

Найдем дисперсию нормальной случайной величины, снова применяя замену z = (x-a)/σ и интегрируя по частям:

DX = M(X-MX)² = = =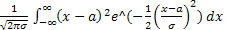

∞

= +

-∞

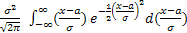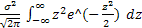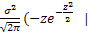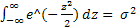
σ² - это дисперсия, а σ – среднее квадратичное отклонение.

50. Дайте определение совместной функции распределения двумерной случайной величины и укажите ее свойства. Обоснуйте эти свойства и/или приведите примеры их выполнения.

Функцией распределения F(x, y) двумерной случайной величины (X, Y) называется вероятность того, что X < x, a Y < y:

F( х, у ) = p ( X < x, Y < y ). (8.1)

y

Рис.1.

Это означает, что точка (X, Y) попадет в область, заштрихованную на рис. 1, если вершина прямого угла располагается в точке (х, у).

Замечание. Определение функции распределения справедливо как для непрерывной, так и для дискретной двумерной случайной величины.

Свойства функции распределения.

1) 0 ≤ F(x, y) ≤ 1 (так как F(x, y) является вероятностью).

2) F(x, y) есть неубывающая функция по каждому аргументу:

F(x₂, y) ≥ F(x₁, y), если x₂ > x₁;

F(x, y₂) ≥ F(x, y₁), если y₂ > y₁.

Доказательство. F(x₂, y) = p(X < x₂, Y < y) = p(X < x₁, Y < y) + p(x₁ ≤ X < x₂, Y < y) ≥

≥ p(X < x₁, Y < y) = F(x₁, y). Аналогично доказывается и второе утверждение.

3) Имеют место предельные соотношения:

а) F(-∞, y) = 0; b) F(x, - ∞) = 0; c) F(- ∞, -∞) = 0; d) F( ∞, ∞) = 1.

Доказательство. События а), b) и с) невозможны ( так как невозможно событие Х<- ∞ или Y <- ∞), а событие d) достоверно, откуда следует справедливость приведенных равенств.

4) При у = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Х:

F(x, ∞) = F₁(x).

При х = ∞ функция распределения двумерной случайной величины становится функцией распределения составляющей Y :

F( ∞, y) = F₂(y).

Доказательство. Так как событие Y < ∞ достоверно, то F(x, ∞) = р(Х < x) = F₁(x). Аналогично доказывается второе утверждение.

Что такое совместный ряд распределений дискретной двумерной случайной величины? Укажите его свойства. Как построить по этому ряду распределения ряды распределения компонент дискретной двумерной случайной величины?

Что такое совместная плотность распределения непрерывной двумерной случайной величины? Укажите ее свойства. Как построить по плотности совместного распределения плотности распределения и функции распределения компонент этой непрерывной двумерной случайной величины?

Плотностью совместного распределения вероятностей (двумер-ной плотностью вероятности) непрерывной двумерной случайной величины называ-ется смешанная частная производная 2-го порядка от функции распределения:

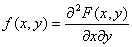. (8.2)

Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δх и Δу к площади этого прямоугольника при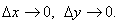

Свойства двумерной плотности вероятности.

1) f(x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).

2) 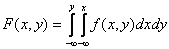(cледует из определения двумерной плотности вероятно-сти).

3) 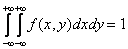(поскольку это вероятность того, что точка попадет на плос-кость Оху, то есть достоверного события).

Как построить бла-бла-бла к сожалению не нашла!

Сформулируйте определение и напишите формулу для вычисления корреляционного момента (коэффициента ковариации) двух случайных величин. Докажите, что для независимых случайных величин его значение равно нулю.

Корреляционным моментом СВ x и h называется мат. ожидание произведения отклонений этих СВ. m x h =М((x —М(x ))*(h —М(h )))

Для вычисления корреляционного момента может быть использована формула:m x h =М(x *h )—М(x )*М(h ) Доказательство: По определению m x h =М((x —М(x ))*(h —М(h ))) По свойству мат. ожидания

m x h =М(x h —М(h )—h М(x )+М(x )*М(h ))=М(x h )—М(h )*М(x )—М(x )*М(h )+М(x )*М(h )=М(x h )—М(x )*(h )

Предполагая, что x и h независимые СВ, тогда m x h =М(x h )—М(x )*М(h )=М(x )*М(h )—М(x )*М(h )=0; m x h =0. Можно доказать, что если корреляционный момент=0, то СВ могут быть как зависимыми, так и независимыми. Если m x h не равен 0, то СВ x и h зависимы. Если СВ x и h зависимы, то корреляционный момент может быть равным 0 и не равным 0. Можно показать, что корреляционный момент характеризует степень линейной зависимости между составляющими x и h . При этом корреляционный момент зависит от размерности самих СВ. Чтобы сделать характеристику линейной связи x и h независимой от размерностей СВ x и h , вводится коэффициент корреляции:

Кx h =m x h /s (x )*s (h ) Коэффициент корреляции не зависит от разностей СВ x и h и только показывает степень линейной зависимости между x и h , обусловленную только вероятностными свойствами x и h . Коэффициент корреляции определяет наклон прямой на графике в системе координат (x ,h ) Свойства коэффициента корреляции.

1. -1<=Кx h <=1

Если Кx h =± 1, то линейная зависимость между x и h и они не СВ.

1. Кx h >0, то с ростом одной составляющей, вторая также в среднем растет.

Кx h <0, то с убыванием одной составляющей, вторая в среднем убывает.

1. D(x ± h )=D(x )+D(h )± 2m x h

Доказательство.

D(x ± h )=M((x ± h )2)—M2(x ± h )=M(x 2± 2x h +h 2)—(M(x )± M(h ))2=M(x 2)± 2M(x h )+M(h 2)—+M2(x )+2M(x )*M(h )—M2(h )=D(x )+D(h )± 2(M(x h ))—M(x )*M(h )=D(x )+D(h )± 2m x h

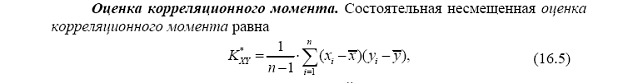
Сформулируйте определение коэффициента корреляции двух случайных величин. Докажите, что его значение не может превышать единицы по абсолютной величине. Докажите, что его значение равно единице по абсолютной величине, если случайные величины связаны линейной зависимостью.