Момент импульса материальной точки. Момент импульса твердого тела

Моментом импульса материальной точки массой m₀ относительно произвольного центра вращения называется векторная величина, равная

, (2.21)

где - радиус вращения, проведенный из центра к началу вектора (рис. 2.4).

О

Рис. 2.4

Так как твердое тело представляет собой совокупность материальных точек массой Dm_i, то момент импульса твердого тела относительно произвольного центра вращения определяется выражением (2.21):

, (2.21а)

где - радиус-вектор, проведенный от центра вращения к началу вектора .

В случае, когда ось вращения твердого тела закреплена и совпадает с осью Z, используется понятие – момент импульса твердого тела относительно оси вращения – (рис. 2.5). Z

] [

] [

Рис. 2.5

Момент импульса каждой материальной точки Dm_i относительно оси Z определяется выражением

(2.22)

где – радиус-вектор, проведенный из центра окружности, по которой движется , к началу вектора .

Момент импульса твердого тела относительно оси Z равен векторной сумме моментов импульсов всех материальных точек:

. (2.23)

Направлен вектор вдоль оси вращения (рис. 2.5). Его направление связано с направлением вращения твердого тела правилом правого винта.

Основной закон динамики вращательного движения

Быстрота изменения момента импульса твердого тела определяется результирующим моментом внешних сил, действующих на тело:

. (2.24)

В проекции на ось 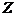, совпадающую с осью вращения:

(2.25)

Равенства (2.24) и (2.25) представляют собой основной закон динамики вращательно движения, записанный в векторной и скалярной формах.

Примеры решения задач

Задача 1. Частица движется так, что зависимость ее радиус-вектора от времени имеет вид

, (3.1)

где А = 2 м/с³, В = 4 м/с², С = -2 м – константы. Найти: 1) модуль мгновенной скорости в момент времени t₁ = 1 с; 2) приращение скорости и среднюю скорость за промежуток времени от t₀ = 0 с до t₂ = 2 с; 3) ускорение частицы и его модуль в момент времени t₂.

Решение.

1) Мгновенную скорость найдем как производную по времени от радиус-вектора, используя закон движения (3.1):

(3.2)

где u_x = 3At², u_y = 2Bt, u_z = 0.

Отсюда получаем

. (3.3)

В момент времени t₁ модуль скорости согласно формуле (3.3) принимает значение u₁ = 10 м/с.

2) Приращение скорости . Используя соотношение (3.2), получим

(3.4)

Чтобы вычислить среднюю скорость < >, найдем выражение для перемещения :

,

которое подставим в формулу, по которой определяется средняя скорость:

(3.5)

После подстановки данных в формулы (3.4) и (3.5) получим:

м/с; м/с.

3) Воспользовавшись зависимостью скорости от времени (3.2), определим мгновенное ускорение как производную от скорости по времени:

. (3.6)

Найдем модуль ускорения

, (3.7)

где согласно (6) а_х = 6At, a_y = 2B, a_z = 0. При t = t₁ формулы (3.6) и (3.7) дают следующие значения:

м/с²; а = 14 м/с².

Ответ:

1) ; u₁ = 10 м/с.

2) ; м/с;

; м/с.

3) ; м/с²;

; а = 14 м/с².

Задача 2. Ускорение точки меняется с течением времени по закону:

, (3.8)

ее начальная скорость

, (3.9)

где А = 2 м/с², с^-1, В = -2 м/с.

Найти: 1) мгновенную скорость точки и ее модуль в момент времени t₁ = 4 с; 2) приращение радиус-вектора (перемещение) точки за время от t₀ = 0 с до t₁ = 4 с; 3) путь, пройденный точкой за это время.

Решение.

1) Зная зависимость ускорения точки от времени, найдем зависимость скорости от времени, воспользовавшись соотношением:

.

Подставив в него заданные выражения для и , получим:

(3.10)

Отсюда ; ; ;

. (3.11)

Таким образом, в любой момент времени модуль скорости одинаков и равен u = 3,3 м/с.

В момент времени t₁ по формуле (3.10) скорость принимает значение (t₁) = (2,5 -2 ) м/с;

2) Для нахождения перемещения воспользуемся соотношением (10):

(3.12)

м.

Из формулы (3.12) ; ; ;

;

м.

3) Найдем длину пути S(t), используя выражение (3.11) для модуля скорости:

. (3.13)

Подставив в (13) данные задачи, получим S(t₁) = 13,2 м.

Ответ:

1) ; (t₁) = (2,5 -2 ) м/с;

; u = 3,3 м/с.

2) ; м.

;

м.

3) ;

S(t₁) = 13,2 м.

Задача 3. Из пушки выпустили последовательно два снаряда со скоростью u₀ = 250 м/с; первый под углом 60°, второй – под углом 30° к горизонту (рис.3.1). Пренебрегая сопротивлением воздуха, найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.

Рис. 3.1

Решение.

Обозначим радиус-вектор и скорость первого снаряда и ,

второго - и , соответственно. Пусть до момента столкновения со времени запуска первого снаряда прошло время t₁, со времени запуска второго снаряда – t₂, а . В момент столкновения положения снарядов совпадают и определяются вектором :

= ₁(t₁)= ₂(t₂). (3.14)

Согласно формуле (1.19),

, ;

или в проекциях на координатные оси (рис.3.1):

x₁(t₁) = u₀ cosα₁ t₁ ;

y₁(t₁) = u₀ sinα₁ t₁ – ; (3.15)

x₂(t₂) = u₀ cosα₂ t₂ ;

y₂(t₂) = u₀ sinα₂ t₂ – . (3.16)

Равенство (3.14) означает, что x₁(t₁) = x₂(t₂) и y₁(t₁) = y₂(t₂). Подставив сюда выражения (3.15), (3.16), получим:

u₀ cosα₁ t₁ = u₀ cosα₂ t₂ (3.17)

u₀ sinα₁ t₁ – = u₀ sinα₂ t₂ – .

Преобразуем последнее уравнение

u₀ (sinα₁ t₁ – sinα₂ t₂ )- (t₁² - t₂²) = 0 (3.18)

Из равенства (3.17) находим

(3.19)

Подставим выражение (3.19) в уравнение (3.18), получим следующее квадратное уравнение:

,

одним из решений которого будет t₂ = 0, что не соответствует условию задачи. Другое решение имеет вид

. (3.20)

Объединяя формулы (3.19) и (3.20), найдем интервал времени между выстрелами:

∆t = 18,7 с.

Ответ:

; ∆t = 18,7 с.

Задача 4.Тангенциальное ускорение точек, лежащих на ободе колеса, меняется с течением времени по закону:

а_t = А + Сt, (3.21)

где А = 2 м/с², С = 4 м/с³ – константы. Найти: 1) угловое ускорение колеса в момент времени t₁ = 2 с; 2) угловую скорость колеса в этот момент времени;

3) зависимость угла поворота колеса от времени; 4) число оборотов, сделанное колесом за 10 с от начала вращения. Радиус колеса 1 м. Угловую скорость и угол поворота в начальный момент принять равными нулю.

Решение.

1) Тангенциальное ускорение точек, лежащих на ободе колеса, и угловое ускорение его вращательного движения связаны соотношением:

а_t = e∙r, где r – расстояние от этих точек до оси вращения, т.е. радиус колеса. Отсюда

. (3.22)

При t = t₁ = 2 c, e = 4 рад/с².

2) Векторы и направлены одинаково, поэтому

, .

Интегрируя последнее выражение с учетом равенства (22), получим:

,

.

Так как по условию задачи в начальный момент времени t = 0 угловая скорость w₀ = 0, последнее выражение принимает вид

. (3.23)

Отсюда w = 12 рад/с при t = t₁ = 2 c.

3) Найдем зависимость угла поворота j от времени, воспользовавшись соотношениями:

, .

Возьмем интеграл от обеих частей последнего равенства с учетом соотношения (3.23):

(3.24)

Отсюда

.

По условию задачи при t = 0 j₀ = 0, поэтому

. (3.25)

4) Угол поворота колеса j и число оборотов N, сделанных колесом за время t, связаны соотношением: j = 2pN. Отсюда с учетом равенства (3.25)

.

Подставляя данные задачи, получим N = 122 об.

Ответ:

1) ; e = 4 рад/с²;

2) ; w = 12 рад/с;

3) ;

4) ; N = 122 об.

Задача 5. Брусок массой m = 20 кг движется вверх по наклонной плоскости с углом наклона α = 30°. На брусок действует сила F = 150 Н под углом β = 30° к плоскости (рис.3.2). Коэффициент трения бруска о плоскость m = 0,2. Найти силу трения, действующую на брусок, ускорение бруска и путь, пройденный им за первые две секунды движения, если начальная скорость равна нулю.

Решение.

На тело действуют четыре силы: тяжести m , трения , реакции опоры и тяги . Второй закон Ньютона (основное уравнение динамики поступательного движения) для тела имеет следующий вид:

. (3.26)

Введем систему координат, в которой ось Х направлена по ускорению бруска, ось Y – перпендикулярно наклонной плоскости вверх вдоль силы реакции опоры (рис. 3.2). Начало координат свяжем с положением бруска на момент времени t₀ = 0 с. Запишем уравнение (3.26) в проекциях на координатные оси Х и Y соответственно:

F cosβ –mg sinα - F_m = ma, (3.27)

F sinβ – mg cosα + F_N= 0. (3.28)

Решив систему уравнений (27) и (28) с учетом соотношения F_m = m F_N, найдем F_m и а:

F_m = m ( mg cosα – F sinβ ); F_m = 19 Н.

; а = 0,641 м/с².

Брусок движется равноускоренно с нулевой начальной скоростью вдоль оси Х, поэтому длина его пути определяется по формуле

; S = 1,28 м.

Ответ:

F_m = m ( mg cosα – F sinβ ); F_m = 19 Н.

; а = 0,641 м/с².

; S = 1,28 м.

Задача 6. Груз массой 2 кг, связанный нерастяжимой нитью, перекинутой через невесомый неподвижный блок, с другим грузом массой 4 кг движется вверх по наклонной плоскости с ускорением 4,8 м/с² (рис. 3.3). Найти силу натяжения нити и коэффициент трения между грузом и плоскостью, если угол наклона плоскости к горизонту α = 30°.

Решение.

На первое тело действуют четыре силы: тяжести , трения , реакции опоры и натяжения нити . На второе тело действуют силы: тяжести и натяжения нити . Запишем уравнения движения грузов в векторной форме:

+ + + = (3.29)

+ = . (3.30)

Поскольку нить нерастяжимая, блок не вращается и трение нити о блок не учитывается, натяжение нити (по модулю) всюду одинаково и модули ускорений тел равны между собой:

F₁ = F₂ = F ; а₁ = а₂ = а (3.31)

Выберем удобную для рассмотрения движения каждого тела систему координат, как показано на рис. 3.3. Найдем с учетом равенств (31) проекции векторов, входящих в уравнения (29) и (30), на координатные оси X₁, Y₁ и Х₂ соответственно:

F – m₁g sinα - F_m = m₁a, (3.32)

-m₁g cosα + F_N = 0, (3.33)

m₂g – F = m₂a. (3.34)

Решая систему уравнений (32)-(34) с учетом равенства F_m = mF_N, найдем:

F = m₂ (g – a); F = 20 Н;

; m = 0,35.

Ответ:

F = m₂ (g – a); F = 20 Н;

; m = 0,35.

Задача 7.На блок диаметра 10 см, укрепленный на горизонтальной оси, проходящей через его центр О, намотана невесомая нить, к концу которой привязан груз массой 300 г (рис. 3.4). Груз проходит расстояние 1 м за время 10 с. Найти момент инерции блока относительно оси вращения. Трением в блоке пренебречь.

Решение.

На груз действуют силы: тяжести m , натяжения нити . Будем рассматривать движение груза относительно системы отсчета, ось Х которой направлена вертикально вниз. Груз движется равноускоренно. Уравнение его движения имеет вид

. (3.35)

На блок действуют силы: тяжести , реакции опоры , натяжения нити . Моменты этих сил относительно оси вращения обозначим , , . Вращение блока будем рассматривать относительно системы отсчета, ось Z которой направлена по оси вращения от нас (рис. 3.4). Блок вращается равноускоренно. Уравнение вращательного движения блока:

= + + .

Моменты сил тяжести и реакции опоры равны нулю, поскольку эти силы проходят через центр вращения О, и, следовательно, плечо каждой из сил равно нулю, поэтому

, (3.36)

т.е. векторы и направлены одинаково – по оси вращения Z от нас.

Перепишем уравнение (3.35) в проекциях на ось Х:

ma = mg – F₁. (3.37)

Спроектируем векторы, входящие в уравнение (3.36), на ось Z:

Je = M₃. (3.38)

Модуль момента силы равен произведению силы F₂ на ее плечо, которое равно половине диаметра блока (рис. 3.4):

. (3.39)

Благодаря невесомости нити силы натяжения и равны по модулю:

F₁ = F₂ = F. (3.40)

Модуль тангенциального ускорения а_t точек блока, соприкасающихся с нитью, равен модулю ускорения нити в любой ее точке, а следовательно, и модулю ускорения груза а: а_t = а. Модуль тангенциального ускорения этих точек и модуль углового ускорения блока связаны соотношением: а_t = , отсюда

. (3.41)

Подставим формулы (3.39) и (3.41) в равенство (3.38). Тогда с учетом выражения (3.40) получим:

. (3.42)

Решив систему уравнений (3.37) и (3.42), найдем:

. (3.43)

Величину ускорения груза можно найти, используя формулу для равноускоренного прямолинейного движения. При условии, что начальная скорость груза u₀ = 0, пройденный путь можно определить по формуле (1.19).

,

откуда .

Подставим последнюю формулу в выражение (43) для момента инерции:

.

Используя данные задачи, получим: J = 0,37 кг∙м².

Ответ:

; J = 0,37 кг∙м².

Задача 8. Груз массой 5 кг, связанный нерастяжимой нитью, перекинутой через неподвижный блок, с другим грузом массой 2 кг, движется вниз по наклонной плоскости (рис. 3.5). Масса блока 300 г. Коэффициент трения между первым грузом и наклонной плоскостью 0,1. Найти ускорение грузов, если угол наклона плоскости к горизонту 30°. Блок считать однородным диском.

Решение.

Заданная система состоит из трех тел: грузов массами m₁ и m₂ и блока массой m₃. Груз m₁ находится под действием сил: тяжести , реакции опоры , натяжения нити и трения . Второй закон Ньютона для этого груза имеет вид

. (3.44)

На груз m₂ действуют силы: тяжести и натяжения нити . Для него второй закон Ньютона имеет вид

. (3.45)

Блок вращается вокруг неподвижной горизонтальной оси, проходящей через центр О. На него действуют силы: тяжести , реакции оси и натяжения нити и . Моменты сил тяжести блока и реакции оси равны нулю. Вращение блока вызывается только действием сил натяжения нити. Поэтому основное уравнение динамики вращательного движения блока следующее:

, (3.46)

где J – момент инерции блока относительно оси вращения; и - моменты сил натяжения нити и относительно центра блока О соответственно.

Векторы и направлены по оси вращения блока: - к нам, - от нас (рис. 3.5). Угловое ускорение по условию задачи направлено также, как и вектор .

Рис. 3.5

Будем рассматривать движение тела m₁ относительно системы отсчета, ось Х₁ которой направлена вдоль ускорения , ось Y₁ – вдоль силы реакции опоры . Перепишем равенство (3.44) в проекциях на эти оси:

m₁a_1x = m₁g sinα – F₁ - F_m , (3.47)

0 = F_N1 - m₁g cosα.

Отсюда F_N1 = m₁g cosα, с учетом этого соотношения сила трения скольжения определяется по формуле: F_m = m m₁ g cosα. Подставив ее в равенство (3.47), будем иметь:

m₁a_1x = m₁g sinα – F₁ - m m₁ g cosα. (3.48)

Движение груза m₂ будем рассматривать относительно системы отсчета, ось Х₂ которой направлена вдоль ускорения (рис. 3.5). Перепишем равенство (3.45) в проекциях на эту ось:

m₂ a_2x = -m₂g + F₂. (3.49)

Для описания вращательного движения блока введем систему отсчета, ось Z которой направлена по оси вращения к нам (рис. 3.5). Перепишем равенство (3.46) в проекциях на эту ось:

Je = M₁ – M₂. (3.50)

Так как блок считается диском, момент инерции блока относительно оси вращения найдем по формуле (2.19). Модули моментов сил и равны произведению соответствующих сил F¢₁ и F¢₂ на их плечи:

M₁ = F¢₁ r; M₂ = F¢₂r. (3.51)

Поскольку нить нерастяжима, ускорения обоих грузов можно считать равными по модулю:

а_1х = а_2х = а. (3.52)

Модуль тангенциального ускорения точек блока, соприкасающихся с нитью, равен модулю ускорения нити в любой ее точке, следовательно, и модулю ускорения грузов. Поэтому а = а_t = er, откуда

e = а / r. (3.53)

Подставив выражения (2.19), (3.51) и (3.53) в формулу (3.50), с учетом соотношения (3.52) получим:

. (3.54)

Решив систему уравнений (3.48), (3.49) и (3.54), будем иметь:

.

Подставив числовые данные, получим: а = 0,09 м/с².

Ответ:

; а = 0,09 м/с².