Динамика вращательного движения твердого тела вокруг неподвижной оси

Основными характеристиками вращательного движения тела являются: момент силы, момент инерции и момент импульса.

Момент силы

Рассмотрим твердое тело произвольной формы, которое может вращаться вокруг закрепленной оси. Пусть на тело действует произвольно направленная сила . Выберем в твердом теле какую-нибудь точку - центр вращения, например, лежащую на оси вращения (рис. 2.2).

] [

d

О

] [

Рис. 2.2

Проведем из нее радиус – вектор в точку приложения силы. Величина определяемая соотношением

, (2.11)

называется моментом силы относительно точки О. Модуль вектора определяется по формуле

, (2.12)

где - угол между векторами и , - длина перпендикуляра, опущенного из центра вращения на линию действия силы. Эта величина называется плечом силы.

В случае, когда твердое тело вращается вокруг закрепленной оси, вращающее действие силы будет характеризоваться величиной, называемой моментом силы относительно этой оси.

Пусть на твердое тело действует произвольно направленная сила , приложенная к телу в точке С (рис. 2.3). Если ось вращения закреплена, то вращающее действие будет оказывать только та составляющая силы , которая лежит в плоскости, перпендикулярной оси вращения, т.е. сила _t (рис. 2.3).

Из точки пересечения указанной плоскости с осью вращения (точки О) проводим радиус-вектор в точку приложения силы _t .

Векторное произведение

(2.13)

будем называть моментом силы относительно оси Z.

Рис. 2.3

Этот вектор всегда направлен по оси вращения и связан с направлением вращения, вызванного силой _t , правилом правого винта.

Модуль момента силы относительно оси Z:

M_z = r∙F_t∙sin α = F_t∙d. (2.14)

Момент инерции твердого тела относительно оси вращения

Момент инерции при вращательном движении имеет тот же смысл, что и масса при поступательном движении. Момент инерции – это мера инертности тела при вращательном движении.

Момент инерции твердого тела зависит от размеров тела, его формы, от распределения плотности материала тела по его объему и от положения оси вращения.

Любое твердое тело представляет собой совокупность материальных точек массой 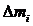, находящихся на расстоянии 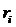от оси вращения. Момент инерции твердого тела относительно оси вращения:

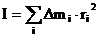(2.15)

Эта формула приближенная. Точной является формула

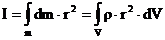. (2.16)

Пользуясь формулой (2.16), можно найти момент инерции 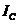однородного тела правильной геометрической формы массой относительно оси, проходящей через центр масс тела :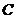

для стержня длиной 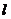(ось перпендикулярна стержню)

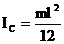; (2.17)

для шара радиуса 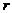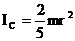; (2.18)

для диска радиуса 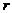(ось перпендикулярна диску)

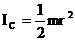. (2.19)

Если ось вращения 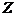не проходит через центр масс, то момент инерции относительно этой оси 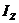определяется по теореме Штейнера:

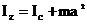. (2.20)

Здесь 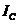- момент инерции тела относительно оси, проходящей через его центр масс параллельно данной оси 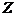, 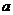- расстояние между осями.