Уравнение вращения тела вокруг неподвижной оси имеет вид

φ = φ(t). (25)

Угловая скорость ω и угловое ускорение ε соответст­венно равны

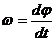(рад/с), (26)

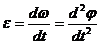(рад/с). (27)

Если в данный момент времени εω > 0, то в этот мо­мент тело вращается ускоренно, если же εω < 0, то вра­щение замедленное.

При вращении тела в одном и том же направлении угол поворота тела φ за промежуток времени t - t₀опре­деляют по формуле

ψ = φ - φ_0, (28)

где φ и φ₀—значения угловой координаты в моменты t и t_0. Угол ψ поворота тела связан с числом оборотов тела N зависимостью

ψ = 2πN . (29)

В технике угловую скорость тела выражают числом оборотов в минуту. Переход от п (об/мин) к ω в (рад/с) осу­ществляют по формуле

ω = πN/30.(30)

При равномерном вращении тела ω = const,ε = 0. В этомслучае уравнение вращения тела имеет вид

φ = φ₀ + ωt. (31)

При равнопеременном вращении тела ε = const. В этом случае

ω = ω₀+ εt, (32)

и уравнение вращения тела принимает вид

φ = φ₀ + ω₀t + εt. (33)

Пример 1. Крен судна на спокойной водe описывается уравнением 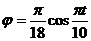(t - в секундах, φ - в радианах), (рис. 35). Определить моменты времени, в которые судно имеет максимальный крен, и моменты, когда его угловая скорость достигает мак­симальных значений, а также промежутки времени, когда вращение судна ускоренное и когда замедленное.

Решение. Для исследования движения определим ω и ε. Согласно формулам (26) и (27),

; .

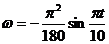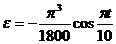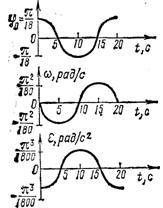
Из уравнения движения судна видно, что максимальный крен судна равен π/18 и имеет место в моменты времени t_п =10 с

(п = 0; 1; 2; ...). В эти моменты времени угловая скорость равна

Рис. 35 нулю, а угловое ускорение имеет экстремальные значения.

Угловая скорость приобретает максимальное значение, равное π²/l80 рад/с в моменты времени t_m = 5 (2m + 1) с (m=0; 1; 2; ...). Рассматриваемое движение имеет периодический характер (период Т = 20 с), поэтому достаточно провести исследование за время одного периода. Из графиков функций следует, что в начальный момент (t = 0) судно имело крен 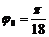, движение началосьбез начальной угловой скорости с угловым ускорением 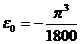рад/с².

В интервале 0 < t < 5 с угловая координата φ уменьшается. Качка судна ускоренная, так как ωε > 0. При t = 5 с угловая ско­рость достигает экстремального значения, а угловое ускорение равно нулю. В интервале 5с< t <10 с вращение судна замедленное. При t = 10 с угловая скорость равна нулю, затем меняет знак, т. е. изме­няется направление вращения судна.

В интервале 10 с < t < 15 с ωε > 0, поэтому вращение ускорен­ное, а в интервале 15c < t < 20c ωε < 0 и вращение снова замед­ленное.

При t = 20 с судно возвращается в первоначальное положение и процесс качки повторяется.

Задачи

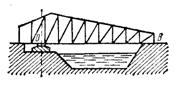1.3.15.* Разводной мост (рис. 36) поворачивается в горизонтальной плоскости на 90°. Считая, что при повороте от 0 до 30° мост вращается равноускоренно, при повороте от 30 до 60°- равномерно и при повороте от 60 до 90° - равнозамедленно, определить время полного пово­рота, если известно, что максимальная скорость конца В равна 1 м/с, а длина

Рис.36 ОВ = 50 м.

Ответ: t = 2 мин 10,7 с.

1.3.16.* При пуске в ход гирокомпаса угловое ускорение его ротора возрастает от нуля пропорционально времени. По прошествии 5 мин ротор имеет 18 000 об/мин. Сколько оборотов сделал ротор за это время?

Ответ: 30000 оборотов.

1.3.17.* В период разгона из состояния покоя угло­вое ускорение ротора турбины за время Т равномерно убывает от начального значения 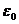до нуля, после чего ротор вращается равномерно. Определить максимальную угловую скорость ротора.

Ответ: ω_тах = ε₀t/2.

1.3.18.* Самолет, летящий с постоянной скоростью и прямолинейным горизонтальным курсом, сопровождается лучом прожектора. С какой угловой скоростью должен поворачиваться луч прожектора, если кратчайшее рас-стоя­ние между прожектором и курсом самолета равно h?

Ответ: ω = 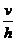cos²φ, где φ - угол между лучом прожектора и перпендикуляром, восставленным из точки нахождения прожектора на курс самолета.

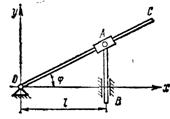1.3.19.*В кулисном механизме (рис. 37) опре­делить угловую скорость и угловое ускорение кулисыОС в момент, когда φ = π/4 рад, если штанга АВ движется с постоянной скоростью и. В начальный момент φ = 0.

Ответ: ; .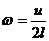

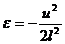Рис.37

1.3.20.* Движение поршня двигателя (рис. 38) задано уравнением s = R sin kt. Определить угловую ско­рость коленчатого вала двигателя в момент, когда поршень занимает среднее положение, если длина шатуна АВ равна L, а длина кривошипа ОА равна R.

Ответ: 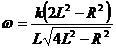; если L>>R,то ω ≈ k.

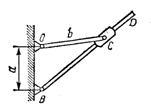
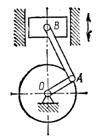
Рис. 38Рис. 39

1.3.21.* Кулисный механизм приводится в движение кривошипом ОС (рис. 39). Определить угловую ско­рость и угловое ускорение кулисы BD, если кривошип ОС вращается с постоянной угловой скоростью ω и в началь­ный момент занимал вертикальное положение, а отноше­ние расстояния между осями О и В к длине кривошипа a/b = λ.

Ответ: ;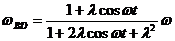

.
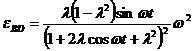