И это равно математическому ожиданию проигрыша второго игрока.

Пусть 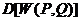есть дисперсия этой случайной величины. Естественно назвать среднее квадратическое отклонение с.в. 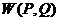, т.е. 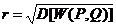риском для первого при игре со стратегиями 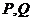. Поскольку выигрыш первого есть проигрыш для второго, то 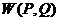есть случайный проигрыш второго и 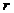вполне естественно можно назвать риском игры с такими стратегиями и для второго.

Предположим сначала, что игроки озабочены только максимизацией среднего дохода за партию игры – обычная цель в таких играх. Тогда игроки будут играть со своими оптимальными стратегиями: 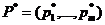– Первый игрок и 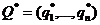– второй, стратегии оптимальны, если М(P,Q*) 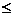М(P*,Q*) 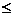М(P*,Q)

Пара (P*,Q*) – решение игры. Математическое ожидание с. в. 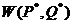называется ценой игры, обозначим ее .

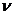Основные понятия в теории графов: дуги, вершины в ориентированном и неориентированном графе. Примеры применения теории графов на практике.

Графом называется пара объектов, состоящая из множества точек и множества отрезков, соединяющих некоторые (может быть, все) из этих точек. Упомянутые точ-ки называются вершинами графа.

Если отрезки, соединяющие вершины графа, имеют направления, то граф называ-ется ориентированным, а сами отрезки — дугами. Если же отрезки не имеют направ-ления, то граф называется неориентированным, и в этом случае говорят, что вершины графа соединены ребрами. Смешанным называется граф, в котором содержатся как ориентированные, так и неориентированные отрезки. Ориентированный граф часто называют сетью.

Обозначим вершины графа 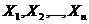, а дугу, соединяющую вершину X_i c X_j - u_ij.

Две дуги графа (два ребра) называются смежными, если они различны и имеют общую вершину. Две вершины графа называются смежными, если существует дуга (ребро), соединяющая их.

Говорят, что дуга исходит из вершины X_i, если X_i является ее началом. Дуга заходит в вершину X_j если X_jявляется ее концом.

Говорят, что в графе данная дуга инцидентна данной вершине, если эта вершина является началом или концом данной дуги.

Путь в ориентированном графе — это последовательность дуг, в которой конец предыдущей дуги совпадает с началом следующей. Путь, в котором ни одна вершина не встречается дважды, называется элементарным. Путь, в котором ни одна дуга не встречается дважды, называется простым, в противном случае — составным. Конечный путь, у которого конечная вершина совпадает с начальной, называется контуром. Контур, образованный одной дугой, называется петлей.

Ориентированный граф называется симметрическим, если любые две смежные вершины его соединены двумя противоположно ориентированными дугами. Ориентированный граф называется антисимметрическим, если каждая пара смежных вершин соединена только в одном направлении и петли отсутствуют.

20) Экономический смысл двойственной задачи к модели оптимального планирования производства. Математическая модель задачи определения расчетных оценок ресурсов.

Теория двойственности является центральной частью всего ЛП. Она имеет богатое экономическое содержание.

В рамках модели ЛП предприятия должна существовать внутренняя система оценки ресурсов, используемых им в процессе производства. Эти оценки связаны с технологическими особенностями данного производственного процесса, характеризуемыми матрицей условий A, со структурой и количеством ресурсов, отпущенных для производственного потребления, описываемых вектором B, а также со структурой внешних цен, на основе которых получается вектор прибылей C. Эти оценки называют расчетными оценками ресурсов. Расчетную оценку единицы ресурса не следует отождествлять с той ценой, по которой предприятию был отпущен этот ресурс. Последняя отражает общественно необходимые затраты на производство единицы ресурса, а расчетная цена показывает только сравнительную ценность этого ресурса на данном предприятии в данных конкретных условиях.

В зависимости от вида исходной задачи линейного программирования различают симметричные и несимметричные пары двойственных задач.

Если система ограничений исходной задачи состоит из неравенств и на все переменные х_j наложено условие неотрицательности, то исходная задача и составленная по определенному правилу двойственная задача образуют симметричную пару двойственных задач.

Пусть исходная задача имеет вид: найти наибольшее значение функции

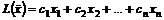
при ограничениях:

.

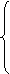
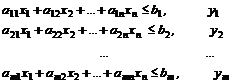
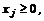
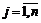Правило составления двойственных задач

1. Каждому ограничению исходной задачи ставится в соответствие двойственная переменная y_i, где .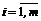

2. Составляется целевая функция 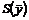, коэффициентами которой будут свободные члены системы ограничений исходной задачи, а цель задачи меняется на противоположную:

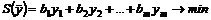. (1)

3. Составляется система ограничений двойственной задачи, при этом матрица из коэффициентов системы ограничений исходной задачи транспонируется, знак неравенства меняется на противоположный, свободными членами будут являться коэффициенты из целевой функции исходной задачи:

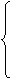
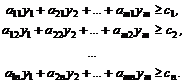₍₂₎

4. Переменные y_i в двойственной задаче также неотрицательны, т.е.

. (3)

Если двойственную задачу принять за исходную и по данному правилу составить двойственную задачу, то получим исходную задачу. Понятие двойственности является взаимным.

В несимметричном случае двойственная задача составляется по тем же правилам, что и в случае симметричной пары, но если двойственная переменная поставлена в соответствие ограничению уравнения, то эта переменная свободна по знаку.