Обратная матрица: определение, свойства, условие существования.

Пусть задана квадратная матрица А. Если существует матрица В, такая что А*В=Е, то говорят что матрица В является обратной по отношению к матрице А: В=А^-1, А*А^-1=Е.

Свойства:

1)Обратная и исходная матрицы перестановочны и матрица, обратная обратной, совпадает с исходной: А*А^-1=А^-1*А=Е.

2)Единственность матрицы: если для данной матрицы обратная мат сущ-т,то она только одна.

Только квадратная матрица может иметь обратную.

Для нахождения обратной матрицы можно использовать следующий алгоритм:

ü Смотрим, квадратная ли матрица: если нет, обратной матрицы не существует; если квадратная, переходим к след. пункту;

ü Вычисляем определитель ∆А; если он равен 0, обратной матрицы не существует; если он не равен 0, переходим к след. пункту;

ü Вместо каждого элемента матрицы ставим его алгебраическое дополнение (алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на (-1)^s, где s – сумма номеров строки и столбца, на пересечении которых расположен этот элемент);

ü Полученную матрицу транспонируем;

ü Каждый элемент полученной матрицы делим на определитель исходной матрицы и получаем матрицу, обратную данной.

14) Постановка линейной производственной задачи, смысл переменных, векторов и матриц, допустимый и оптимальный план, математическая модель.

Многие проблемы, возникающие в экономических исследованиях, планировании и управлении, будучи сформулированными математически, представляют собой задачи, в которых необходимо решить систему линейных алгебраических уравнений или неравенств и среди всех неотрицательных решений найти то решение, при котором линейная однородная функция принимает наибольшее или наименьшее значение. Изучение методов исследования и решения математических задач указанного типа составляет содержание раздела математики, кот. принято называть линейным программированием.

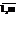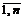Предположим, что предприятие выпускает n видов продукции при использовании m видов ресурсов. Известны: технологическая матрица расходов i-го вида ресурса на единицу j-го вида продукции – А=(а_ij), где i= ; j= . Матрица запаса ресурсов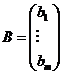

Известны прибыль, полученная предприятием от производства и реализации продукции j-го вида. Требуется составить план производства продукции: x = (x₁, x₂, x₃,...x_n), при котором предприятие получит наибольшую прибыль. Суммарная прибыль предприятия 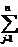c_j x_j. Требуется среди всех решений системы уравнений (1) найти такое неотрицательное решение, при котором линейная форма (3) принимает наименьшее возможное значение.

Любое неотрицательное значение системы называют допустимым, а допустимое решение, при котором целевая ф-я принимает наименьшее значение – оптимальным решением задачи ЛП.

Ограничения по ресурсам записываются в виде:

а₁₁x₁ + a₁₂x₂ + … a_1nx_n ≤ b₁

а₂₁x₁ + a₂₂x₂ + … a_2nx_n ≤ b₂

. . . . .

а_m1x₁ + a_m2x₂ + … a_mnx_n ≤ b_m.

где b_i-запас ресурса iго вида, x₁≥0, x₂≥0, ...x_n≥0.

Математическая модель задачи выглядит следующим образом: найти производственную программу (x₁, x₂, x₃, x₄), максимизирующую прибыль z = 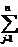c_j x_j → max, если переменная x_j удовлетворяет следующим ограничениям: a_ijx_j ≤ b_i; x_j≥ 0; i= 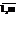; j= .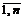

Если в матем-й модели какой-либо задачи планирования будут содержаться линейные неравенства, то их можно заменить линейными уравнениями с помощью дополнительных неотрицательных неизвестных.