История и свойства последовательности.

Введение.

Фибоначчи Леонардо Пизанский ( 1180-1240) — это первый крупный математик средневековой Европы.

Более известный под прозвищем Фибоначчи (Fibonacci), что в переводе с итальянского означает «хороший сын родился» (Figlio Buono Nato Ci).

О бытие Фибоначчи известно немного. Неизвестна даже точная дата его рождения. Предполагается, что Фибоначчи родился предположительно в 1170 г.

Жизнь и научная карьера Леонарда теснейшим образом связана с развитием европейской культуры и науки.
В

век Фибоначчи возраждение было еще далеко, однако история даровала Италии краткий промежуток времени, который вполне можно было назвать репетицией надвигающейся эпохи Ренессанса. Этой репетицией руководил Фридрих 2, император (с 1220 года) "Священной Римской империи Германской Нации". Воспитанный в традициях южной Италии Фридрих II был внутренне глубоко далек от европейского христианского рыцарства. Поэтому к преподаванию в основанном им Неаполитанском университете, наряду с христианскими учеными, он привлек арабов и евреев.
Столь любимые его дедом рыцарские турниры, на которых сражающиеся калечили друг друга на потеху публике, Фридрих II совсем не признавал. Вместо этого он культивировал гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами.
На таких турнирах и заблистал талант Леонарда Фибоначчи. Этому способствовало хорошее образование, которое дал сыну купец Боначчи, взявший его с собой на Восток и приставивший к нему арабских учителей.
Впоследствии Фибоначчи пользовался неизменным покровительством Фридриха II.
Это покровительство стимулировало выпуск научных трактатов Фибоначчи: обширнейшей "Книге абака", написанной в 1202 году, но дошедшей до нас во втором своем варианте, который относится к 1228 г.; "Практики геометрии"( 1220г.); "Книги квадратов"(1225г.). По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, математику учили чуть ли не до времен Декарта ( 17 в.).

Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.

Наибольший интерес представляет сочинение "Книга абака". Эта книга представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течение нескольких следующих

столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами и узнали преимущества использования индо - арабской системой исчисления по сравнению с римской.

Раковина.

Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Cпирали очень распространены в природе. Раковина в форме спирали - форма раковины заинтересовала Архимеда и он выяснил, что увеличение длины завитков раковины – это постоянная величина и равна она 1,618.

Золотые" спирали широко распространены в биологическом мире. Рога баранов, коз, антилоп и других рогатых животных растут лишь с одного конца. Этот рост осуществляется по спирали.

И не только в раковине моллюска и рогах животных можно найти спирали Фибоначчи, а во многих цветах и растениях, просто они не такие явные.

Растения и животные.

Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Cовместная работа ботаников и математиков пролила свет на эти удивительные явления природы. Выяснилось, что в расположении листьев на ветке семян подсолнечника, шишек сосны проявляет себя ряд Фибоначчи, а стало быть, проявляет себя закон золотого сечения. Паук плетет паутину спиралеобразно. Cпиралью закручивается ураган. Испуганное стадо северных оленей разбегается по спирали. Молекула ДНK закручена двойной спиралью. Гете называл спираль "кривой жизни".
Cреди придорожных трав растет ничем не примечательное растение - цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий - 38, четвертый - 24 и т.д. Длина лепестков тоже подчинена золотой пропорции.

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции - длина её хвоста так относится к длине остального тела, как 62 к 38. 0,62 к 0,38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы - симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.
Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

А если взглянуть чуть подальше, то можно разглядеть последовательность Фибоначчи в недосягаемых галактиках.

В Тихом океане имеются звезды астеридеи с 8 лучами, звезда мохнатая имеет 13 лучей. Морская звезда гелиастер (подсолнух) имеет 33 луча, а пламенистая звезда - 55. Таким образом, у многих морских звезд количество лучей задается числами Фибоначчи или близкими к ним числами.

Числа Фибоначчи и цветы.

Белая калла – 1лепесток

Молочай – 2 лепестка

Триллиум – 3 лепестка.

Лилии и ирисы имеют тоже по три лепестка.

Водосбор – 5 лепестков

Волчья стопа – 8 лепестков

Черноглазая Сьюзан.

Хризантема – 21 лепесток

Некоторые астры тоже имеют по 21 лепестку.

Введение.

Фибоначчи Леонардо Пизанский ( 1180-1240) — это первый крупный математик средневековой Европы.

Более известный под прозвищем Фибоначчи (Fibonacci), что в переводе с итальянского означает «хороший сын родился» (Figlio Buono Nato Ci).

О бытие Фибоначчи известно немного. Неизвестна даже точная дата его рождения. Предполагается, что Фибоначчи родился предположительно в 1170 г.

Жизнь и научная карьера Леонарда теснейшим образом связана с развитием европейской культуры и науки.
В

век Фибоначчи возраждение было еще далеко, однако история даровала Италии краткий промежуток времени, который вполне можно было назвать репетицией надвигающейся эпохи Ренессанса. Этой репетицией руководил Фридрих 2, император (с 1220 года) "Священной Римской империи Германской Нации". Воспитанный в традициях южной Италии Фридрих II был внутренне глубоко далек от европейского христианского рыцарства. Поэтому к преподаванию в основанном им Неаполитанском университете, наряду с христианскими учеными, он привлек арабов и евреев.
Столь любимые его дедом рыцарские турниры, на которых сражающиеся калечили друг друга на потеху публике, Фридрих II совсем не признавал. Вместо этого он культивировал гораздо менее кровавые математические соревнования, на которых противники обменивались не ударами, а задачами.
На таких турнирах и заблистал талант Леонарда Фибоначчи. Этому способствовало хорошее образование, которое дал сыну купец Боначчи, взявший его с собой на Восток и приставивший к нему арабских учителей.
Впоследствии Фибоначчи пользовался неизменным покровительством Фридриха II.
Это покровительство стимулировало выпуск научных трактатов Фибоначчи: обширнейшей "Книге абака", написанной в 1202 году, но дошедшей до нас во втором своем варианте, который относится к 1228 г.; "Практики геометрии"( 1220г.); "Книги квадратов"(1225г.). По этим книгам, превосходящим по своему уровню арабские и средневековые европейские сочинения, математику учили чуть ли не до времен Декарта ( 17 в.).

Роль его книг в развитии математики и распространении в Европе математических знаний трудно переоценить.

Наибольший интерес представляет сочинение "Книга абака". Эта книга представляет собой объемный труд, содержащий почти все арифметические и алгебраические сведения того времени и сыгравший значительную роль в развитии математики в Западной Европе в течение нескольких следующих

столетий. В частности, именно по этой книге европейцы познакомились с индусскими ("арабскими") цифрами и узнали преимущества использования индо - арабской системой исчисления по сравнению с римской.

История и свойства последовательности.

Фибоначчи Леонардо Пизанский — это первый крупный математик средневековой Европы. Более известен под прозвищем Фибона́ччи (Fibonacci), что в переводе с итальянского означает «хороший сын родился» (Figlio Buono Nato Ci).

О бытие Фибоначчи известно немного. Неизвестна даже точная дата его рождения. Предполагается, что Фибоначчи родился предположительно в 1170 г.

Леонардо Фибоначчи был знаменитым итальянским математиком, он славился своим умением делать расчеты. Однажды его осенило и он открыл простую последовательность чисел, соотношения между которыми описывали естественные пропорции всех тел вселенной!

Плоды математических трудов учёного применяются во многих науках, искусстве и повседневной жизни по сей день.

Заслугой Леонардо Фибоначчи является ряд чисел Фибоначчи. Считается, что об этом ряде было известно на Востоке, но именно Леонардо Фибоначчи опубликовал этот ряд чисел в книге «Liber Abaci» (сделал он это для демонстрации размножения популяции кроликов).

Последовательность Фибоначчи, известная всем по фильму "Код Да Винчи" - ряд цифр, описанный в виде загадки Итальянским математиком Леонардо Пизанским, более известным под прозвищем Фибоначчи, в XIII в. Вкратце суть загадки:

Кто-то поместил пару кроликов в некоем замкнутом пространстве, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что каждый месяц пара кроликов производит на свет другую пару, а способность к производству потомства у них появляется по достижению двухмесячного возраста.

Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр.

Ряд чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55и т.д. известен как ряд Фибоначчи.

Так как первая пара в первом месяце дает потомство, удвой, и в этом месяце окажутся 2 пары; из них одна пара, а именно первая, рождает и в следующем месяце, так что во втором месяце оказывается 3 пары; из них в следующем месяце 2 пары будут давать потомство, так что в третьем месяце родятся еще 2 пары кроликов, и число пар кроликов в этом месяце достигнет 5; из них в этом же месяце будут давать потомство 3 пары, и число пар кроликов в четвертом месяце достигнет 8; из них 5 пар произведут другие 5 пар, которые, сложенные с 8 парами, дадут в пятом месяце 13 пар; из них 5 пар, рожденных в этом месяце, не дадут в том же месяце потомство, а остальные 8 пар рождают, так что в шестом месяце оказывается 21 пара; сложенные с 13 парами, которые родятся в седьмом месяце, они дают 34 пары; сложенные с 21 парой, рожденной в восьмом месяце, они дают в этом месяце 55 пар; сложенные с 34 парами, рожденными в десятом месяце, они дают 89 пар; сложенные вновь с 55 парами, которые рождаются в десятом месяце, они дают в этом месяце 144 пары; снова сложенные с 89 парами, которые рождаются в одиннадцатом месяце, они дают в этом месяце 233 пары; сложенные вновь с 144 парами, рожденными в последнем месяце, они дают 377 пар; столько пар привела первая пара в данном месте к концу одного года.

Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д.

· При делении каждого числа на следующее за ним через одно получаем число 0,382; наоборот – соответственно 2,618.

· Подбирая таким образом соотношения, получаем основной набор Фибоначчиевских коэффициентов: … 4.235, 2.618, 1.618, 0.618, 0.382, 0.236. Все они играют особую роль в природе, и в частности – в техническом анализе.

· Отношение каждого числа к последующему более и более стремится к 0.618 по увеличении порядкового номера. Отношение же каждого числа к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют (ФИ).

Фибоначчи по сути не открыл ничего нового, он просто напомнил миру о таком явлении, как Золотое Сечение, которое не уступает по значимости теореме Пифагора.

Все окружающие нас предметы мы различаем в том числе и по форме. Какие-то нам нравятся больше, какие-то меньше, некоторые вовсе отталкивают взгляд. Иногда интерес может быть продиктован жизненной ситуацией, а порой красотой наблюдаемого объекта. Симметричная и пропорциональная форма, способствует наилучшему зрительному восприятию и вызывает ощущение красоты и гармонии. Целостный образ всегда состоит из частей разного размера, находящихся в определённом соотношении друг с другом и целым.

Важно отметить, что Фибоначчи как бы напомнил свою последовательность человечеству. Она была известна еще древним грекам и египтянам. И действительно, с тех пор в природе, архитектуре, изобразительном искусстве, математике, физике, астрономии, биологии и многих других областях были найдены закономерности, описываемые коэффициентами Фибоначчи.

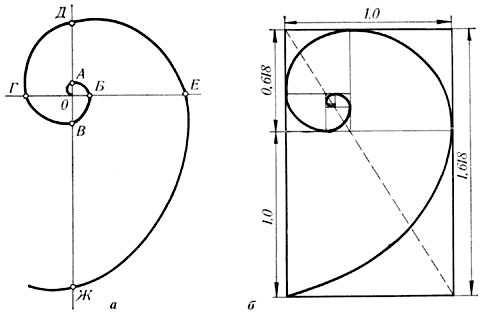
Например, число 0.618 представляет собой постоянный коэффициент в так называемом золотом сечении (рис.1), где любой отрезок делится таким образом, что соотношение между его меньшей и большей частью равно соотношению между большей частью и всем отрезком. Таким образом, число 0.618 известно еще как золотой коэффициент или золотая середина. Такого типа пропорцию можно встретить абсолютно везде (рис.2).

Рисунок 1. Золотое сечение

Рисунок 2. Примеры соотношений Фибоначчи

Золотое сечение - высшее проявление совершенства целого и его частей в науке, искусстве и природе.

Определение золотого сечения

Деление отрезка в среднем и крайнем отношении называют золотым сечением. В истории утвердилось ещё одно название – «золотая пропорция». Пусть, С АВ, и производит, как говорят, «золотое сечение» отрезка АВ.

АС: АВ =СВ: АС (1)

Золотым сечением называется такое деление отрезка, при котором большая часть так относится к целому, как меньшая часть к большей.

Если мы примем весь отрезок АВ за 1, то отрезок АС будет равен 0,618, отрезок ВС - 0,382, только так будет соблюдено условие Золотого Сечения (0,618:0,382=1,618; 1:0,618=1,618). Отношение АС:ВС равно 1,618, а АВ: АС равно 2,618. Это всё те же, уже знакомые нам, коэффициенты Фибоначчи.

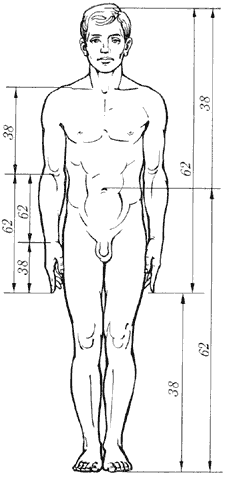
Пропорции человеческого тела во многих соотношениях близки к Золотому Сечению.

Золотая пропорция и тело человека

Древние скульпторы знали и использовали золотую пропорцию как критерий гармонии, канон красоты, корни которой лежат в пропорциях человеческого тела. “Человеческое тело – лучшая красота на земле”, - утверждал Н.Чернышевский. Эталонами красоты человеческого тела, образцами гармонического телосложения издавна и по праву считаются великие творения греческих скульпторов: Фидия, Поликлета, Мирона, Праксителя. В создании своих творений греческие мастера использовали принцип золотой пропорции. Центр золотой пропорции строения человеческого тела располагался точно на месте пупка. И не случайно величину золотой пропорции принято обозначать буквой Ф; это сделано в честь Фидия – творца бессмертных скульптурных произведений.