Распределение Дарбина-Уотсона.
Критические точки 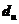 (
( 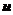 означает upper – верхняя) и
означает upper – верхняя) и 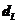 (
( 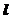 означает low – нижняя) при уровне значимости
означает low – нижняя) при уровне значимости 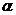 = 0,5(
= 0,5( 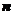 - объем выборки,
- объем выборки, 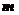 - число объясняющих переменных в уравнении регрессии).
- число объясняющих переменных в уравнении регрессии).
(Критерий Дабина-Уотсонаявляется наиболее известным критерием обнаружения автокорреляции первого порядка)
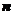 | 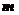 =1 =1 | 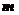 = 2 = 2 | 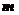 = 3 = 3 | 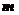 = 4 = 4 | ||||
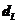 | 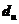 | 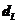 | 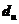 | 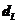 | 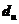 | 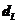 | 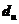 | |
| 0,610 | 1,400 | |||||||
| 0,700 | 1,356 | 0,467 | 1,896 | |||||
| 0,763 | 1,332 | 0,359 | 1,777 | 0,368 | 2,287 | |||
| 0,824 | 1,320 | 0,629 | 1,699 | 0,435 | 2,128 | 0,296 | 2,388 | |
| 0,879 | 1,320 | 0,697 | 1,641 | 0,525 | 2,016 | 0,376 | 2,414 | |
| 0,927 | 1,324 | 0,658 | 1,604 | 0,595 | 1,928 | 0,444 | 2,283 | |
| 0,971 | 1,331 | 0,812 | 1,579 | 0,658 | 1,864 | 0,512 | 2,177 | |
| 1,010 | 1,340 | 0,861 | 1,562 | 0,715 | 1,816 | 0,574 | 2,094 | |
| 1,045 | 1,330 | 0,905 | 1,551 | 0,767 | 1,779 | 0,632 | 2,030 | |
| 1,077 | 1,361 | 0,946 | 1,543 | 0,814 | 1,750 | 0,685 | 1,977 | |
| 1,106 | 1,371 | 0,982 | 1,539 | 0,857 | 1,728 | 0,734 | 1,935 | |
| 1,133 | 1,381 | 1,015 | 1,536 | 0,897 | 1,710 | 0,779 | 1,900 | |
| 1,158 | 1,391 | 1,046 | 1,535 | 0,933 | 1,696 | 0,820 | 1,872 | |
| 1,180 | 1,401 | 1,074 | 1,536 | 0,967 | 1,685 | 0,859 | 1,848 | |
| 1,201 | 1,411 | 1,100 | 1,537 | 0,998 | 1,676 | 0,894 | 1,828 | |
| 1,221 | 1,420 | 1,125 | 1,538 | 1,026 | 1,669 | 0,927 | 1,812 | |
| 1,239 | 1,429 | 1,147 | 1,541 | 1,053 | 1,664 | 0,958 | 1,797 | |
| 1,257 | 1,437 | 1,168 | 1,543 | 1,078 | 1,660 | 0,986 | 1,785 | |
| 1,273 | 1,446 | 1,188 | 1,546 | 1,101 | 1,656 | 1,013 | 1,775 | |
| 1,288 | 1,454 | 1,206 | 1,550 | 1,123 | 1,654 | 1,038 | 1,767 | |
| 1,302 | 1,461 | 1,224 | 1,553 | 1,143 | 1,652 | 1,062 | 1,759 | |
| 1,316 | 1,469 | 1,240 | 1,556 | 1,162 | 1,651 | 1,084 | 1,753 | |
| 1,328 | 1,476 | 1,255 | 1,560 | 1,181 | 1,650 | 1,104 | 1,747 | |
| 1,341 | 1,483 | 1,270 | 1,563 | 1,198 | 1,650 | 1,124 | 1,743 | |
| 1,352 | 1,489 | 1,284 | 1,567 | 1,214 | 1,650 | 1,143 | 1,739 | |
| 1,363 | 1,496 | 1,297 | 1,570 | 1,229 | 1,650 | 1,160 | 1,735 | |
| 1,373 | 1,502 | 1,309 | 1,574 | 1,244 | 1,650 | 1,177 | 1,732 | |
| 1,383 | 1,508 | 1,321 | 1,577 | 1,258 | 1,651 | 1,193 | 1,730 | |
| 1,393 | 1,514 | 1,333 | 1,580 | 1,271 | 1,652 | 1,208 | 1,728 | |
| 1,402 | 1,519 | 1,343 | 1,584 | 1,283 | 1,653 | 1,222 | 1,726 | |
| 1,411 | 1,525 | 1,354 | 1,587 | 1,295 | 1,654 | 1,236 | 1,724 | |
| 1,419 | 1,530 | 1,364 | 1,590 | 1,307 | 1,655 | 1,249 | 1,723 | |
| 1,427 | 1,535 | 1,373 | 1,594 | 1,318 | 1,656 | 1,261 | 1,722 | |
| 1,435 | 1,540 | 1,382 | 1,597 | 1,328 | 1,658 | 1,273 | 1,722 | |
| 1,442 | 1,544 | 1,391 | 1,600 | 1,338 | 1,659 | 1,285 | 1,721 | |
| 1,503 | 1,585 | 1,462 | 1,628 | 1,421 | 1,674 | 1,378 | 1,721 | |
| 1,583 | 1,641 | 1,554 | 1,672 | 1,525 | 1,703 | 1,494 | 1,735 | |
| 1,654 | 1,694 | 1,634 | 1,715 | 1,613 | 1,736 | 1,592 | 1,758 | |
| 1,720 | 1,746 | 1,706 | 1,760 | 1,693 | 1,774 | 1,679 | 1,788 | |
| 1,758 | 1,778 | 1,748 | 1,789 | 1,738 | 1,799 | 1,728 | 1,810 |
Приложение 8
Критические значения количества рядов для определения наличия
автокорреляции по методу рядов ( 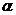 = 0,05)
= 0,05)
Нижняя граница 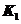
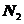 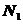 | |||||||||||||||||||
верхняя граница 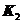
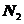 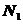 | |||||||||||||||||||
Пример: пусть 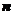 = 20 и знаков «+» 11 (=
= 20 и знаков «+» 11 (= 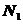 ) и знаков «-» 9 (=
) и знаков «-» 9 (= 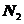 ). Тогда при
). Тогда при 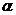 = 0,05 нижняя граница
= 0,05 нижняя граница 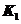 =6, верхняя граница
=6, верхняя граница 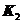 = 16. если наблюдаемое значение
= 16. если наблюдаемое значение 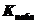
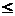 6 или
6 или 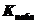
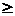 16, то гипотеза об отсутствии автокорреляции должна быть отклонена.
16, то гипотеза об отсутствии автокорреляции должна быть отклонена.
Приложение 9
Таблица значений функции Пуассона: 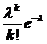
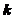 | 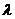 | ||||||||
| 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| 0,9048 | 0,8187 | 0,7408 | 0,6703 | 0,6065 | 0,5488 | 0,4966 | 0,4493 | 0,4066 | |
| 0,0905 | 0,1638 | 0,2222 | 0,2681 | 0,3033 | 0,3293 | 0,3476 | 0,3595 | 0,3696 | |
| 0,0045 | 0,0164 | 0,0333 | 0,0536 | 0,0758 | 0,0988 | 0,1217 | 0,1438 | 0,1647 | |
| 0,0002 | 0,0011 | 0,0033 | 0,0072 | 0,0126 | 0,0198 | 0,0284 | 0,0383 | 0,0494 | |
| - | - | 0,0002 | 0,0007 | 0,0016 | 0,0030 | 0,0050 | 0,0077 | 0,0111 | |
| - | - | - | 0,0001 | 0,0002 | 0,0004 | 0,0007 | 0,0012 | 0,0020 | |
| - | - | - | - | - | - | 0,0001 | 0,0002 | 0,0003 |
Приложение 10
Таблица значений 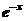
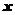 | 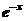 | 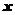 | 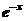 | 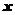 | 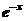 |
| 0,1 | 0,9048 | 2,1 | 0,1224 | 4,1 | 0,0166 |
| 0,2 | 0,8187 | 2,2 | 0,1108 | 4,2 | 0,0150 |
| 0,3 | 0,7408 | 2,3 | 0,1002 | 4,3 | 0,0135 |
| 0,4 | 0,6703 | 2,4 | 0,0907 | 4,4 | 0,0123 |
| 0,5 | 0,6065 | 2,5 | 0,0821 | 4,5 | 0,0111 |
| 0,6 | 0,5488 | 2,6 | 0,0743 | 4,6 | 0,0100 |
| 0,7 | 0,4966 | 2,7 | 0,0672 | 4,7 | 0,0091 |
| 0,8 | 0,4493 | 2,8 | 0,0608 | 4,8 | 0,0082 |
| 0,9 | 0,4066 | 2,9 | 0,0550 | 4,9 | 0,0074 |
| 1,0 | 0,3679 | 3,0 | 0,0498 | 5,0 | 0,0067 |
| 1,1 | 0,3329 | 3,1 | 0,0450 | 5,1 | 0,0061 |
| 1,2 | 0,3012 | 3,2 | 0,0476 | 5,2 | 0,0055 |
| 1,3 | 0,2725 | 3,3 | 0,0369 | 5,3 | 0,0050 |
| 1,4 | 0,2466 | 3,4 | 0,0334 | 5,4 | 0,0045 |
| 1,5 | 0,2231 | 3,5 | 0,0302 | 5,5 | 0,0041 |
| 1,6 | 0,2019 | 3,6 | 0,0273 | 5,6 | 0,0037 |
| 1,7 | 0,1827 | 3,7 | 0,0247 | 5,7 | 0,0033 |
| 1,8 | 0,1653 | 3,8 | 0,0224 | 5,8 | 0,0030 |
| 1,9 | 0,1496 | 3,9 | 0,0202 | 5,9 | 0,0027 |
| 2,0 | 0,1353 | 4,0 | 0,0183 | 6,0 | 0,0025 |
Приложение 11
Равномерно распределенные случайные числа
Список литературы
1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник для вузов. М.: ЮНИТИ, 1998.
2. Бабешко Л.О. Основы эконометрического моделирования: Учебное пособие. Изд. 3-е, стереотипное, - М.: КомКнига, 2007.
3. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление /Пер. с англ./ - М.: Мир, 1974.
4. Бородич С.А. Эконометрика: Учеб. Пособие / С.А. Бородич. – 2-е изд., испр. – Мн.: Новое знание, 2004.
5. Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. Изд. 7-е, стер. – М.: Высш. шк., 1999.
6. Груббер Й. Эконометрия. В 2 т. Т. 1:Введение в эконометрию. К.,1996. 397 с.
7. Доугерти К. Введение в эконометрику. – М.: ИНФРА-М., 2001.
8. Дуброва Т.А. Статистические методы прогнозирования: Учебно-практическое пособие / МЭСИ. М., 1999.
9. Капельян С.Н., Левкович О.А. Основы коммерческих и финансовых расчетов / НТЦ АПИ. Минск, 1999.
10. Катышев П.К., Магнус Я.Р., Пересецкий А.А. Сборник задач к начальному курсу эконометрики. – 3-е изд., испр. – М.: Дело, 2003.
11. Красс М.С., Чурпынов Б.П. Математика для экономистов.–СПб.: Питер, 2007.
12. Кремер Н.Ш., Путко Б.А. Эконометрика: Учебник для вузов / Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ-ДАНА, 2002.
13. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: Начальный курс. М.: Дело, 2000.
14. Практикум по Эконометрике: Учебное пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2006.
15. Просветов Г.И. Эконометрика: Задачи и решения: Учебно-методическое пособие. 3-е изд., доп. – М.: Издательство РДЛ, 2006.
16. Тихомиров Н.П., Дорохина Е.Ю. Эконометрика: учебник / Н.П. Тихомиров, Е.Ю. Дорохина – М.: Издательство «Экзамен», 2003.
Оглавлениестр.
Предисловие ----------------------------------------------------------------------------------- 3
Введение ----------------------------------------------------------------------------------- 5
Глава 1. Основные понятия. Общие вопросы эконометрического
моделирования. Проблемы прогнозирования. ------------------------------------- 9
1.1. Основные понятия, перекрестные данные и временные ряды, генеральная совокупность и выборка. Выборочный метод. Способы отбора. ------------------- 9
1.2.Общие вопроси моделирования. Критерии «хорошей» модели.
Основные допущения прогнозирования и причины ошибки прогнозов. ----------- 12
