Задачи на теоремы сложения и умножения вероятностей

40. Экспедиция издательства отправила газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе - 0,9, в третье - 0,8. Найти вероятность следующих событий:

а) только одно отделение получит газеты вовремя;

б) хотя бы одно отделение получит газеты с опозданием.

Ответ:а) 0,032; б) 0,316.

41. Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.

Ответ:0,14.

42. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Ответ:0,8.

43. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Ответ: .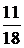

44. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятности:

а) двойного попадания;

б) двойного промаха;

в) хотя бы одного попадания;

г) одного попадания.

Ответ:а) 0,72; б) 0,02; в) 0,98; г) 0,26.

45. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8. Найти вероятности того, что формула содержится

1) только в одном справочнике;

2) только в двух справочниках;

3) во всех трех справочниках.

46. Вероятности попадания в цель при стрельбе из трех орудий равны соответственно 0,7; 0,8 и 0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Ответ: 0,994.

47. В типографии имеется четыре печатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина.

Ответ: 0,9999.

48. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз?

Ответ: не менее 5.

49. В трамвайном парке имеются 15 трамваев маршрута №1 и 10 трамваев маршрута №2. Какова вероятность того, что вторым по счету на линию выйдет трамвай маршрута №1?

Ответ: 0,6.

50. Какова вероятность того, что 2 карты, вынутые из колоды в 36 карт, окажутся одной масти?

Ответ: .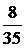

51. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.

Ответ:0,135.

52. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Ответ:0,628.

53. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго.

а) Каков процент брака на конвейере?

б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере?

Ответ:а) 0,04; б) 0,33; 0,39; 0,28.

Задачи на теоремы Лапласа (Муавра-Лапласа), Пуассона

54. В жилом доме имеется 6400 ламп, вероятность включения каждой из них в вечернее время равна 0,5. Найти вероятность того, что число одновременно включенных ламп будет между 3120 и 3200. Найти наивероятнейшее число включенных ламп и его соответствующую вероятность.

Ответ: .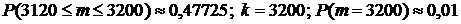

55. Вычислительное устройство состоит из 1000 элементов, работающих независимо друг от друга. Вероятность отказа каждого элемента за смену равна 0,024. Найти вероятность, что за смену откажут 6 элементов.

Ответ: 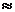0,000083.

56. Найти вероятность того, что если бросить монету 200 раз, то орел выпадет от 90 до 110 раз.

Ответ: 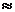0,2952.

57. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени T равна 0,002. Найти вероятность того, что за время T откажут ровно три элемента.

Ответ: 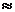0,18.

58. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути 0,004. Найти вероятность того, что в пути повреждено меньше трех изделий.

Ответ: 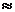0,68.

59. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит более двух разбитых бутылок.

Ответ: 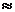0,5678.

60. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 280 деталей отличного качества.

Ответ: 0,0032.

61. В продукции некоторого производства брак составляет 15%. Изделия отправляются потребителям (без проверки) в коробках по 100 штук. Найти вероятности событий:

B – наудачу взятая коробка содержит 13 бракованных изделий;

С – число бракованных изделий в коробке не превосходит 20.

Ответ: 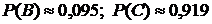.