Числовые хар-ки выборочного распр.: выборочное среднее, выборочная дисперсия, медиана, ассиметрия, эксцесс, выборочные моменты.

В этом вопр вмето S надо сигма d ???

Пусть случ. эксперимент описывается СВ Х.

Повторяя случ. эксперимент n раз, получим посл-сть наблюденных знач. x1, x2, …, xn СВ Х, называемых выборкой из ген. сов-сти Ωx, описываемой ф-цией распр. F(x). Опр.: Выборочным средним наблюденных знач. выборки назыв. вел-на, определяемая по формуле 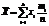, где xi – наблюденное значение с частотой mi, n – число наблюдений, 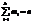. Частоты mi могут быть равны 1, i = 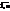, тогда k=n. Опр.: Стат. дисперсией 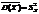выборочного распр. назыв. среднее арифметическое квадратов отклонений знач. наблюдений от средней арифметической , т.е. 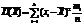, где xi – наблюденное значение с частотой mi', 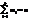, n – число наблюдений. В кач-ве числовой хар-ки выборки так же применяется медиана. Чтобы вычислить ее все наблюдения располагают в порядке возрастания или убывания. При этом, если число вариант нечетно, т.е. 2m+1, то медианой является m+1 варианта ( 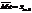); если же число вариант четное, то медиана равна среднему арифметическому двух средних знач.: 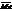= (xm+xm+1)/2. Хар-ка ассиметрии выборочного распр. вычисляется по формуле 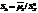, а эксцесс выборочного распр. определяется характеристикой 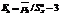. Обобщающими хар-ками выборочных распр. являются стат. моменты распр.. Начальные стат. моменты k-того порядка: 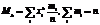. Тогда: при k =0 M0 = 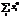(mi/n) = 1; при k =1 M1 = 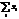( mi/n) = 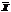; при k =2 M2 = 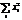( mi/n) = 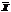2; при k =3 M3 = 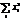( mi/n) = 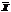3; при k =4 M4 = 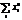( mi/n) = 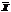4 и т.д. Практически используются моменты первых четырех порядков. Центр. стат. моменты k-того порядка: 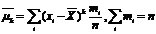. Тогда: при k =0 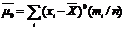=1; при k =1 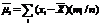=0; при k =2 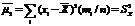- стат. дисперсия; при k =3 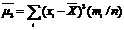; при k =4 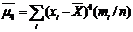и т.д. Отметим, что центр. стат. момент 3-его порядка служит мерой ассиметрии распр. выборки. Если распр. симметрично, то 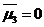. На практике моменты порядка выше четвертого почти не применяются, т.к. обладают очень высокой дисперсией и их сколько-нибудь надежное опр. потребовало бы выборок большого объема.

47. Понятие оценки параметра. Св-ва оценок: состоятельность, несмещенность, эффективность.

Пусть требуется подобрать распр. для исследуемой СВ Х по выборке x₁, x₂, …, x_n , извлеченной из ген. сов-сти Ω_x с неизвестной ф-цией распр. F(x). Выбрав распр., исходя из анализа выборки, мы по данным выборки должны оценить параметры соотв. распр.. Например, для нормального распр. можно опр. параметры m и σ; для распр. Пуассона — параметр λ и т.д. Решение вопросов о «наилучшей» оценке неизвестного параметра и составляет теорию стат. оценивания. Выборочная числовая хар-ка, применяемая для получения оценки неизвестного параметра ген. сово-сти, называется оценкой параметра. Например, Х – среднее арифм. может служить оценкой мат. ожидания M(X) ген. сов-сти Ω_x. В принципе для неизвестного параметра a может существовать много числовых хар-ик выборки, которые вполне подходящи для того, чтобы служить оценками. Например, среднее арифметическое, медиана, мода могут показаться вполне приемлемыми для оценивания мат. ожидания M(X) сово-сти. Чтобы решить, какая из статистик в данном мн-ве наилучшая, необходимо определить некоторые желаемые св-ва таких оценок, т.е. указать условия, которым должны удовлетворять оценки. Опр.: Если M( 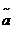) =a, то 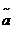называется несмещенной оценкой а. В других случаях говорят, что оценка смещена. Если существует больше одной несмещенной оценки, то выбирают более эффективную оценку, т.е. ту, для которой вел-на второго момента M( 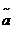- а)² меньше. Опр.: Оценка 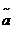₁ называется более эффективной, чем оценка 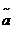₂, если M( 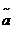₁ - а)² <M( 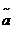₂ - а)² . При использовании той или иной оценки желательно, чтобы точность оценивания увеличилась с возрастанием объема производимой выборки. Предельная точность будет достигнута в том случае, когда численное знач. оценки совпадает со знач. параметра при неограниченном увеличении объема выборки. Такие оценки будем называть состоятельными. Опр.: Оценка 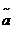называется состоятельной оценкой а, если при n→∞ она сходится по вероятности к а.