Случайные величины. Закон распределения. Ряд распределения дискретной случайной величины. Смешанная случайная величина.

Под случайной величиной понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение. Возможные значения случайной величины образуют множество Ξ, которое называется множеством возможных значений случайной величины. Обозначения случайной величины: X, Y, Z; возможные значения случайной величины: x, y, z.В зависимости от вида множества Ξ случайные величины могут быть дискретными и недискретными. СВ Х называется дискретной, если множество ее возможных значений Ξ – счетное или конечное. Если множество возможных значений СВ несчетно, то такая СВ является недискретной.В теоретико-множественной трактовке основных понятий теории вероятностей случайная величина Х есть функция элементарного события: X=φ(ω), где ω – элементарное событие, принадлежащее пространству Ω. При этом множество Ξ возможных значений СВ Х состоит из всех значений, которые принимает функция φ(ω).

Закон распределения случайной величины.Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной. (То есть, всякое соотношение, устанавливающее связь между возможными значениями СВ и их вероятностями.)СВ будет полностью описана с вероятностной точки зрения, если мы зададим это распределение, т.е. в точности укажем, какой вероятностью обладает каждое событие. Про случайную величину мы будем говорить, что она подчинена данному закону распределения.

X	x1	x2	…	xn	…
P	p1	p2	…	pn	…

Ряд распределения дискретной случайной величины.Наиболее простую форму можно придать закону распределения дискретной случайной величины. Рядом распределения дискретной случайной величины называется таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины X: x₁, x₂, …, x_n, … и вероятности этих значений p₁, p₂, …, p_n, …, где p_i=P{X=x_i} – вероятность того, что в результате опыта СВ Х примет значение x_i (i=1,2,…, n, …).Ряд распределения записывается в виде таблицы:

Так как события {X=x1}, {X=x2}, … несовместны и образуют полную группу, то сумма всех вероятностей, стоящих в нижней строке равна единице:

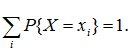Смешанная случайная величина.

Случайная величина называется смешанной, если функция распределения F(x) на некоторых участках непрерывна, а в отдельных точках имеет разрывы (скачки).

На тех участках, где F(x) непрерывна, вероятность каждого отдельного значения случайной величины равна нулю. Вероятность тех значений, где функция распределения совершает скачки, отличны от нуля и равны величине скачка.

7.Функция распределения случайной величины и ее свойства.Функциейраспределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x:

F(x)=P{X<x}.

Геометрически функция распределения интерпретируется как вероятность того, что случайная точка X попадет левее заданной точки X (рис. 5.1). Из геометрической интерпретации наглядно можно вывести основные свойства функции распределения.

1. 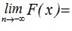F(-¥ ) = 0. (5.2)

2. 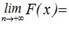F(+¥ ) = 1. (5.3)

3.F(x) – неубывающая функция своего аргумента, т.е. при x₁ < x₂

F(x₁) £ F(x₂).

Доказательство этого свойства иллюстрируется рис. 5.2.

Представим событие C={X<x₂} как сумму двух несовместных событий С=A+B, где A={X<x₁} и B={x₁£X<x₂}.

По правилу сложения вероятностей

P(C)=P(A)+P(B),

т.е. P{X<x₂}=P{X<x₁}+P{ x₁£X<x₂}, или

F(x₂)=F(x₁)+P{x₁£X<x₂}.

Но P{x₁£X<x₂}£0, следовательно, F(x₁) £ F(x₂)

4. P(α£ X < β) = F(β) - F(α), для "[α,β[ÎR. (5.4)

Доказательство этого свойства вытекает из предыдущего доказательства.Вероятность того, что случайная величина Х в результате опыта попадет на участок от α до β (включая α) равна приращению функции распределения на этом участке.Таким образом, функция распределения F(x)любой случайной величины есть неубывающая функция своего аргумента, значения которой заключены между 0 и 1: 0≤F(x)≤1, причем F(-∞)=0, F(+∞)=1.

8.Непрерывная случайная величина. Плотность распределения случайной величины и ее свойства.

Случайная величина Х называется непрерывной, если ее функция распределения F(x) есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.Так как для таких случайных величин функция F(x) нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю

P{X=α}=0 для любого α.В качестве закона распределения, имеющего смысл только для непрерывных случайных величин существует понятие плотности распределения или плотности вероятности.

Вероятность попадания непрерывной случайной величины X на участок от x до x+Dx равна приращению функции распределения на этом участке:

P{x£ X <x+Dx}=F(x+Dx) - F(x).

Плотность вероятности на этом участке определяется отношением

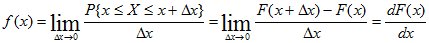(5.6)

Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.

Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Эта величина называется элементом вероятности.

Вероятность попадания случайной величины X на произвольный участок [a, b[ равна сумме элементарных вероятностей на этом участке:

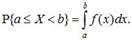(5.7)

В геометрической интерпретации P{α≤X<β} равна площади, ограниченной сверху кривой плотности распределения f(x) и опирающейся на участок (α,β) (рис. 5.4).

Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:

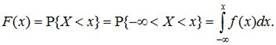(5.8)

В геометрической интерпретации F(x) равна площади, ограниченной сверху кривой плотности распределения f(x) и лежащей левее точки x (рис. 5.5).

Основные свойства плотности распределения:

1. Плотность распределения неотрицательна: f(x) ³ 0.

Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной.

2. Условие нормировки: 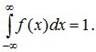Это свойство следует из формулы (5.8), если положить в ней x=∞.

Геометрически основные свойства плотности f(x) интерпретируются так:1.вся кривая распределения лежит не ниже оси абсцисс;2полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

1. 9. Числовые характеристики случайных величин.Математическое ожидание. Свойства математического ожидания.

Законы распределения случайной величины являются исчерпывающими характеристиками. Каждый закон распределения представляет собой некоторую функцию, указание которой полностью описывает случайную величину с вероятностной точки зрения.

Однако часто закон распределения неизвестен и приходится ограничиваться меньшими сведениями; зачастую достаточно бывает только отдельные числовые параметры, характеризующие отдельные черты распределения; например, среднее значение или разброс случайной величины («степень случайности»). Такие числа называются числовыми характеристиками случайной величины.

Рассмотрим случайную величину Y, зависящую функционально от случайной величины X с известным законом распределения F(x): Y=φ(X).

Если Х – дискретная случайная величина и известен ее ряд распределения имеет вид:

Xi	x1	x2	…	xn
pi	p1	p2	…	pn

φ(X)i	φ(x1)	φ(x2)	…	φ(xn)
pi	p1	p2	…	pn

Определяем вероятности появления различных значений случайной величины У

Тогда математическое ожидание случайной величины Y определяется так:

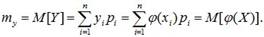(9.1)

Если случайная величина X непрерывна и имеет плотность распределения f(x), то заменяя в формуле (9.1) вероятности p_i элементом вероятности f(x)dx, а сумму – интегралом, получаем:

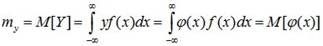. (9.2)

Для смешанной случайной величины выражение для математического ожидания преобразуется к виду:

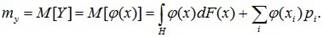(9.3)

Соотношения (9.1), (9.2) и (9.3) – общее понятие математического ожидания, позволяющее вычислить математическое ожидание для неслучайных функций случайного аргумента.

Математическое ожидание (МО) характеризует среднее взвешенное значение случайной величины.

Для вычисления математического ожидания для ДСВ каждое значение x_i учитывается с «весом», пропорциональным вероятности этого значения.

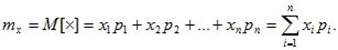(6.1)

M[X]-оператор математического ожидания;

m_x -- число, полученное после вычислений по формуле.

Для НСВ заменим отдельные значения 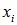непрерывно изменяющимся параметром 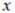, соответствующие вероятности 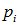- элементом вероятности 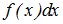, а конечную сумму – интегралом: 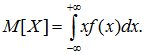(6.2)

Механическая интерпретация понятия математического ожидания: на оси абсцисс расположены точки с абсциссами 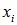, в которых сосредоточены соответственно массы р₁, р₂,...., причем 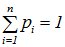. Тогда МО – абсцисса центра тяжести. Для НСВ – масса распределена непрерывно с плотностью .

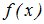Для смешанных случайных величин математическое ожидание состоит из двух слагаемых.

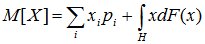, (6.3)

где сумма распространяется на все значения x_i, имеющие отличные от нуля вероятности, а интеграл – на все участки оси абсцисс, где функция распределения F(x) непрерывна.

Физический смысл математического ожидания – это среднее значение случайной величины, т.е. то значение, которое может быть использовано вместо конкретного значения, принимаемого случайной величиной в приблизительных расчетах или оценках.